Identification of Hydrogeological Parameter in Double-Porosity Fractured Aquifer Based on Single-Well Pumping Test
-
摘要: 为探究双重介质含水层中单孔抽水试验水文地质参数求取方法，在不考虑井储效应的双重介质非达西流模型基础上，提出了考虑井储效应的双重介质非达西流模型，并以某野外试验场中实地进行的单孔抽水试验为例，比较了不同求参方法对单孔抽水试验参数识别的效果.结果表明，使用考虑井储的双重介质非达西流模型，反演结果与实测水位降深的吻合度最高；考虑非达西流态，更加适用于抽水流量大，地下水流场呈现非达西流的状态；考虑井储效应，能够更好地刻画出抽水过程前期地下水位迅速下降的现象；考虑双重介质结构，能够更好地刻画出抽水过程前‒中期孔隙‒裂隙介质间水量交换作用由弱变强的现象.说明本文提出的考虑井储效应的双重介质非达西流模型具有一定的适用性.Abstract: To find out a suitable equation for single-well pumping test in double-porosity aquifer, it takes wellbore storage effect into consideration and present the double-porosity non-Darian model with wellbore storage effect based on double-porosity non-Darcian model in this study. Taking a single-well pumping test as an example, the results show that the simulation curve has the highest accuracy when using the double-porosity non-Darcian model proposed in this study; taking non-Dacian effect into consideration is more suitable when the pumping rate is relatively large and the flow in aquifer shows non-Darcian property. When considering non-Darcian effect, we can have a better inversion of the instantaneous drawdown in early time; when regarding the aquifer as double-porosity, we can portray the weak to strong process of the water exchange in fracture and porosity media. In that case, the double-porosity non-Darcian model with wellbore storage effect presented in this study is suitable for single-well pumping test in double-porosity aquifer.
-
图 1 不同模型水位降深s-抽水时间t曲线
Fig. 1. Drawdown-time curve of observation well using different models
图 6 不同模型对单孔抽水试验的拟合结果
Fig. 6. Curve-fit graph of single-well pumping test using different models
表 1 抽水孔代表性岩心及含水层划分
Table 1. Representative lithology and aquifer division of the hydrogeology in pumping well
岩性分层 层深（m） 地层岩性 岩心照片 含水层划分 1 0~39.5 J3ch1b凝灰岩 
风化裂隙水，水量小 风化裂隙含水层 2 39.5~306 J3ch1b凝灰岩 
相对隔水层 3 306~320 J3ch1b凝灰岩 
断层破碎带，涌水段 承压含水层 4 320~520 J3ch1b凝灰岩 
相对隔水层 
下载: 导出CSV
表 2 不同模型对单孔抽水试验的拟合结果
Table 2. Curve fit results of single-well pumping test using different models
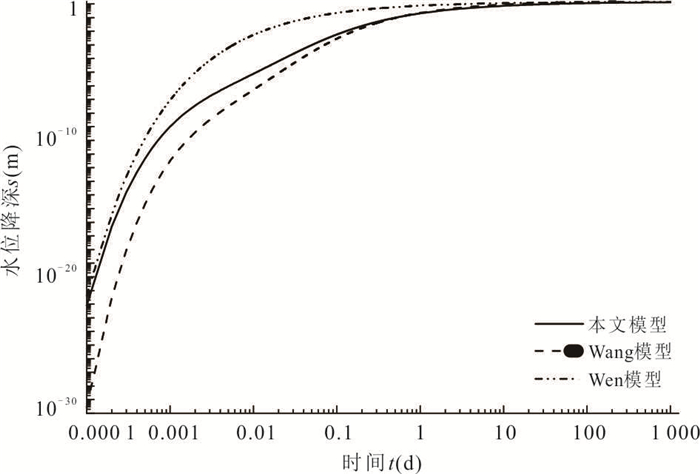
拟合结果 选用模型 考虑井储效应 不考虑井储效应 双重介质非达西流 双重介质达西流 均质含水层非达西流（Wen模型） 双重介质非达西流（Wang模型） Theis模型 n 1.117 1 1.248 1.098 1 Kq（m/s）n 7.207×10‒6 2.37×10‒5 2.35×10‒6 9.32×10‒6 2.28×10‒5 Sf（-）f 0.049 92 0.022 53 - 0.023 75 - Sm（-） 0.478 3 0.225 5 0.239 8 0.237 5 0.489 C（s‒1） 16.02 11.95 - 2.44 - RMSE 0.194 7 0.214 9 0.329 2 0.242 9 0.303 8
下载: 导出CSV
-
Barenblatt, G. I., Zheltov, Y. P., Kochina, I. N., 1960. Basic Concepts in the Theory of Seepage of Homogeneous Liquids in Fissured Rocks. Journal of Applied Mathematics, 24(5): 1286-1303. Bordier, C., Zimmer, D., 2000. Drainage Equations and Non-Darcian Modelling in Coarse Porous Media or Geosynthetic Materials. Journal of Hydrology, 228(3/4): 174-187. https://doi.org/10.1016/S0022-1694(00)00151-7 De Smedt, F., 2011. Analytical Solution for Constant-Rate Pumping Test in Fissured Porous Media with Double-Porosity Behaviour. Transport in Porous Media, 88(3): 479-489. https://doi.org/10.1007/s11242-011-9750-9 Fenske, P. R., 1977. Radial Flow with Discharging-Well and Observation-Well Storage. Journal of Hydrology, 32(1-2): 87-96. https://doi.org/10.1016/0022-1694(77)90120-2 Forchheimer, P. H., 1901. Wasserbewegun Durch Boden. Zeitschrift des Vereines Deutscher Ingenieure, 50: 1781-1788. https://doi.org/10.1016/0022-1694(77)90120-2 He, L. Q., Huang, K., Wan, J. W., et al., 2015. High-Resolution Identification of Hydrogeological Parameters in Dual-Aqueous Medium. Geological Science and Technology Information, 34(1): 216-220 (in Chinese with English abstract). Huang, K., Sun, R. L., Yuan, S. Q., et al., 2022. Effect of Number of Pumping Tests and Prior Information on Hydraulic Conductivity Estimation of Three-Dimensional Heterogeneous Aquifer. Earth Science, 47(2): 689-699 (in Chinese with English abstract). Izbash, S., 1931. O Filtracii Krupnozernistom Materiale. Izv Nauchnoissled Inst. Gidrotechniki (NIIG), Leningrad. Kazemi, H., Seth, M. S., Thomas, G. W., 1969. The Interpretation of Interference Tests in Naturally Fractured Reservoirs with Uniform Fracture Distribution. Society of Petroleum Engineers Journal, 9(4): 463-472. doi: 10.2118/2156-B Li, C., Wang, N. T., Hu, C., et al., 2020. Hydrogeological Parameter Determination of the Confined Aquifer under Confined-Unconfined Conditions by Means of Multiple-Well Pumping Test. Safety and Environmental Engineering, 27(4): 1-7 (in Chinese with English abstract). Li, N., 2020. The Formation Mechanism and Hydrogeological Parameters of Karst Thermal Water: A Case Study of Nanyang Thermal Spring in Xingshan County of Hubei Province, Xiangxi River Basin (Dissertation). China University of Geosciences, Wuhan (in Chinese with English abstract). Li, X., Su, S. L., Wen, Z., et al., 2022. Numerical Analysis of Estimating Groundwater Velocity through Single-Well Push-Pull Test. Earth Science, 47(2): 633-641 (in Chinese with English abstract). Li, Z. X., Wan, J. W., Zhan, H. B., et al., 2019. Particle Size Distribution on Forchheimer Flow and Transition of Flow Regimes in Porous Media. Journal of Hydrology, 574: 1-11. https://doi.org/10.1016/j.jhydrol.2019.04.026 Moench, A. F., 1984. Double-Porosity Models for a Fissured Groundwater Reservoir with Fracture Skin. Water Resources Research, 20(7): 831-846. https://doi.org/10.1029/WR020i007p00831 Stehfest, H., 1970a. Algorithm 368: Numerical Inversion of Laplace Transforms. Communications of the ACM, 13(1): 47-49. https://doi.org/10.1145/361953.361969 Stehfest, H., 1970b. Remark on Algorithm 368: Numerical Inversion of Laplace Transforms. Communications of the ACM, 13(10): 624. https://doi.org/10.1145/355598.362787 Wan, J. W., Huang, K., Chen, C. X., 2013. Reassessing Darcy' Law on Water Flow in Porous Media. Earth Science, 38(6): 1327-1330 (in Chinese with English abstract). Wang, Y. L., Zhan, H. B., Huang, K., et al., 2021. Identification of Non-Darcian Flow Effect in Double-Porosity Fractured Aquifer Based on Multi-Well Pumping Test. Journal of Hydrology, 600: 126541. https://doi.org/10.1016/j.jhydrol.2021.126541 Warren, J. E., Root, P. J., 1963. The Behavior of Naturally Fractured Reservoirs. Society of Petroleum Engineers Journal, 3(3): 245-255. https://doi.org/10.2118/426-pa Wen, Z., Huang, G. H., Zhan, H. B., et al., 2008. Two-Region Non-Darcian Flow toward a Well in a Confined Aquifer. Advances in Water Resources, 31(5): 818-827. https://doi.org/10.1016/j.advwatres.2008.01.014 Wen, Z., Wang, Q. R., 2013. Approximate Analytical and Numerical Solutions for Radial Non-Darcian Flow to a Well in a Leaky Aquifer with Wellbore Storage and Skin Effect. International Journal for Numerical and Analytical Methods in Geomechanics, 37(11): 1453-1469. https://doi.org/10.1002/nag.2091 何林青, 黄琨, 万军伟, 等, 2015. 双重含水介质水文地质参数的高分辨率识别. 地质科技情报, 34(1): 216-220. 黄康, 孙蓉琳, 袁淑卿, 等, 2022. 抽水组数和先验信息对估算三维非均质含水层渗透系数的影响. 地球科学, 47(2): 689-699. doi: 10.3799/dqkx.2021.013 李丞, 王宁涛, 胡成, 等, 2020. 利用多孔抽水试验确定承压‒无压流条件下承压含水层的水文地质参数. 安全与环境工程, 27(4): 1-7. 李娜, 2020. 香溪河流域岩溶热水成因模式及水文地质参数反演研究——以湖北省兴山县南阳温泉为例(博士学位论文), 武汉: 中国地质大学. 李旭, 苏世林, 文章, 等, 2022. 单井注抽试验测算地下水流速的数值分析. 地球科学, 47(2): 633-641. doi: 10.3799/dqkx.2021.102 万军伟, 黄琨, 陈崇希, 2013. 达西定律成立吗. 地球科学, 38(6): 1327-1330. doi: 10.3799/dqkx.2013.000 -
魏世毅 ES-2021-0612.R2 附图一.zip
-
点击查看大图
图(6) / 表(2)
计量
- 文章访问数: 14
- HTML全文浏览量: 14
- PDF下载量: 0
- 被引次数: 0
