用面积平衡原理预测伸展断陷盆地中岩层内部应变及亚分辨正断层的方法

漆家福; GroshongR H Jr; 杨桥

用面积平衡原理预测伸展断陷盆地中岩层内部应变及亚分辨正断层的方法

1.
教育部石油天然气成藏机理重点实验室, 北京 102249
2.
Department of Geological Sciences, the University of Alabama, USA

基金项目:

国家自然科学基金项目 49872068

详细信息

作者简介:
漆家福(1957-), 男, 教授, 现从事油区构造解析、沉积盆地分析方向的研究工作

中图分类号: P618.130.2;P542
计量
- 文章访问数: 3556
- HTML全文浏览量: 451
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2002-08-12
- 刊出日期: 2002-11-25

Analysis Method for Predicting Strain of Interior Beds and Sub-Resolution Faults from Area-Balance Theory in Extensional Basin

1.
KeyLaboratory for Hydrocarbon Accumulation, Ministry of Education, Beijing 102249, China
2.
Department of Geological Sciences, the University of Alabama, USA

摘要

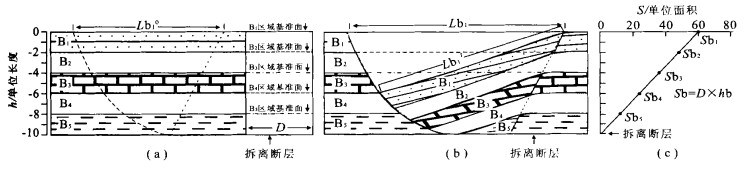
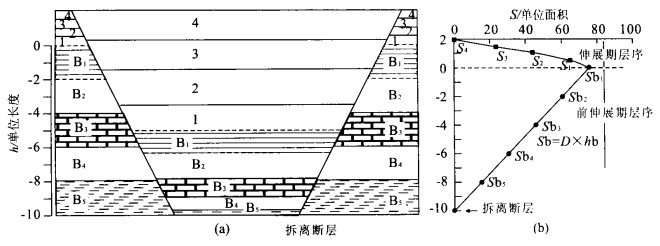
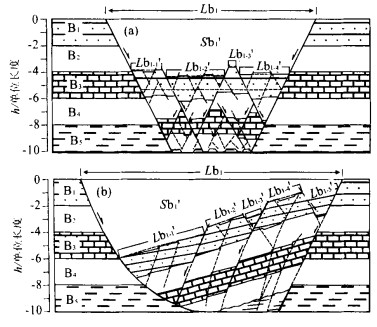
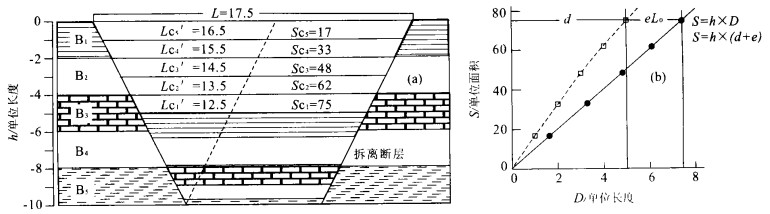
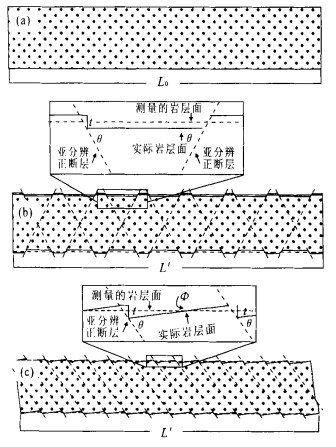
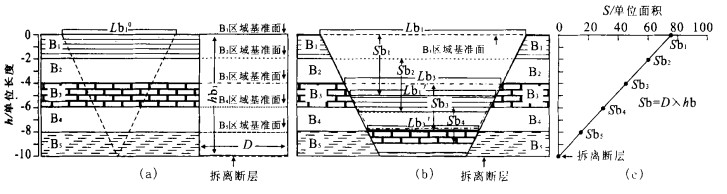
摘要: 大多数地堑和半地堑是由深度近水平的拆离正断层控制的.根据面积平衡原理, 这些伸展断陷盆地岩层的区域基准面至拆离断层面高度(h) 与其损失面积(S) 呈线性比例.拆离断层之上的盆地基底岩层的水平伸展量相同, 因此, 用“S -h图解法”可以确定拆离断层深度, 并能在此基础上计算出岩层的总水平伸展量.伸展盆地中的总水平伸展量主要是由不同尺度的正断层的水平离距体现出来的.可观测解释的断层的水平位移可以通过测量盆地宽度、岩层长度等直接得到.用剖面面积平衡方法可计算出盆地各岩层的平行岩层面的应变, 其中相当部分是由在观测尺度上不能直接解释出来的“亚分辨正断层”的小尺度位移造成的.因此, 在分析伸展断陷盆地的构造样式、岩层力学性质基础上, 有可能对计算得到的平行岩层的伸展应变进行合理评估, 进而可以定量地预测“亚分辨正断层”的密度和可能的分布部位.
- 面积平衡 /
- 伸展应变 /
- 亚分辨断层 /
- 地堑 /
- 半地堑 /
- S-h图解
Abstract: Extensional basin includes mainly graben and half-graben controlled by low detachment. Based on the area-balance theory, there is a linear equation between a height of regional to detachment (h) on the outside of the basin and lose area (S) of the regional in extensional basin. The basement beds above detachment are of same extensional displacement so that "S-h diagram" can be used to determine the depth to detachment and to calculate the total extensional displacement of the beds above detachment. The extensional displacement is dominated by the heave of various scale normal faults. The displacement of obvious faults can be immediately figured out by measured bed-length. The requisite displacement calculated by area balance is the layer-parallel strain, which could be the extensional displacement of sub-resolution faults. Accordingly, the layer-parallel strain can help us to predict the magnitude and distribution of sub-resolution fault on the base of analysis of structural style and rheological behaviour.
- area-balance /
- extensional strain /
- sub-resolution fault /
- graben /
- half-graben /
- S-h diagram

HTML全文

图 1 拆离断层上盘的地堑模型及其“S-h图解”

Fig. 1. Model of a full-graben developed above detachment and its "S-h diagram"

下载: 全尺寸图片幻灯片

图 2 拆离断层上盘的半地堑模型及其“S-h图解”

Fig. 2. Model of a half-graben developed above detachment and its "S-h diagram"

下载: 全尺寸图片幻灯片

图 3 生长地堑模型及其“S-h图解”

Fig. 3. Model of a growth graben developed above detachment and its "S-h diagram"

下载: 全尺寸图片幻灯片

图 4 发育有次级调节正断层的地堑与半地堑模型

a.地堑; b.半地堑

Fig. 4. Models of full-graben and half-graben with accommodation faults

下载: 全尺寸图片幻灯片

图 5 同沉积地堑盖层层序模型及其“S-D图解”

Fig. 5. Model of cover beds in a growth graben and its "S-D diagram"

下载: 全尺寸图片幻灯片

图 6 岩层内部亚分辨正断层形成伸展应变的2种模型

a.原始岩层; b.共轭亚分辨正断层模型; c.多米诺式亚分辨正断层模型

Fig. 6. Two models of extensional strain caused by sub-resolution normal faults

下载: 全尺寸图片幻灯片

表 1 测量和计算图 1所示地堑的基底岩层的构造参数

Table 1. Structural data of basement beds measured and calculated from graben model in Fig. 1

表 2 测量和计算图 3所示地堑的盖层岩层的剖面构造数据

Table 2. Structural data of cover beds measured and calculated from graben model in Fig. 3

参考文献(9)

[1]	Boxter K. The role of small-scale extensional faulting in the evolution of basin geometries, an example from the Late Paleozoic Petrel sub-basin, Northwest Australia[J]. Tectonophysics, 1998, 287: 21-41. doi: 10.1016/S0040-1951(98)80059-0
[2]	Groshong R H Jr. Area balance, depth to detachment and strain in extension[J]. Tectonics, 1994, 13: 1488-1497. doi: 10.1029/94TC02020
[3]	Groshong R H Jr. Construction and validation of extensional cross sections using lost area and strain, with application to the Rhine graben[A]. In: Buchanan P G, Niewland D A, eds. Modern developments in structural interpretation, validation and modeling[C]. London: Geological Society, 1996. 79-98.
[4]	Groshong RHJr, Pashin J C, Schneeeflock R D. Sub-resolution fault strain in a gulf of Mexico growth graben: predictions from area balance conformed by 3-D seismic[EB/OL]. http://www.AAPG.org/datasystems/abstract/13annual/0291.
[5]	Qi J F, Pashin J C, Groshong RHJr. Structural and evolution of North Choctaw Ridge Field, Alabama, a salt-related footwall uplift along the perpheral fault system, Gulf Coast basin[J]. Gulf Coast Association of Geological Societies Transactions, 1998, 48: 349-359.
[6]	陆克政, 漆家福, 戴俊生, 等. 渤海湾新生代含油气盆地构造模式[M]. 北京: 地质出版社, 1987. LU K Z, QI J F, DAI J S, et al. Tectonic model of the Cenozoic petroliferous basin in Bohai Bay basins[M]. Beijing: Geological Publishing House, 1987.
[7]	Walsh J J, Watterson J, Yielding G. The importance of smallscale faulting in regional extension[J]. Nature, 1991, 351: 391-393. doi: 10.1038/351391a0
[8]	Nical A, Walsh J J, Gillespie P A, et al. Fault size distributions—are they really power law[J]. Journal of Structural Geology, 1996, 18: 191-197. doi: 10.1016/S0191-8141(96)80044-7
[9]	漆家福, 杨桥, 童亨茂, 等. 构造因素对半地堑盆地的层序充填的影响[J]. 地球科学——中国地质大学学报, 1997, 22(6): 603-608. QI J F, YANG Q, TONG HM, et al. Sequence construction response to tectonic process in extensional half-graben basin[J]. Earth Science—Journal of China University of Geosciences, 1997, 22(6): 603-608.