Theory on Coupling of Radial Flow in a Confined Aquifer and Bending of Confining Unit
-
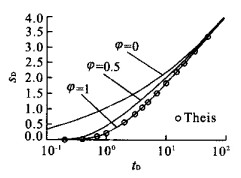
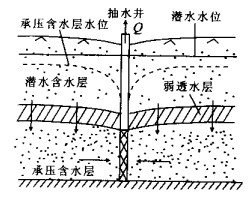
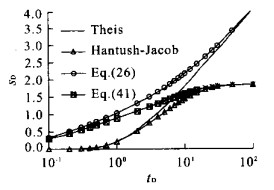
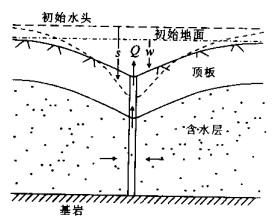
摘要: 指出承压含水层盖层的弯曲变形与开采井周围的径向地下水运动存在相互作用, 而这一效应在传统的井流理论中没有被认识到.通过引入弹性薄板理论, 建立了无越流的承压含水层井流-顶板弯曲效应的解析模型, 同时考虑了含水层和水的压缩性, 结果表明Theis井流方程给出的抽水降深偏小.在此基础上推导了有越流承压含水层井流-盖层弯曲效应的偏微分方程, 求出了解析解, 并与传统理论的结果进行了对比, 表明Hantush-Jacob公式计算的降深也是偏小的.在抽水井附近和抽水初期, 传统理论可能导致显著的相对误差.Abstract: The non-steady radial flow surrounding a pumping well in a fully confined or leaky confined aquifer will induce the bending of confining unit, and then the radial flow patterns are affected by the bending effect through reducing of total stress.However, in conventional theory of groundwater flow, this interaction was omitted. In this study, the elastic plate theory was introduced to establish the analytical models of coupling of radial flow in a confined aquifer and bending of the confining unit, and meanwhile both of non-leaky and leaky conditions were considered as well as the compressibility of skeleton and water. It was indicated by the analytical solutions of the new theory that Theis equation underestimated the drawdown for fully confined aquifers. For leaky confined aquifers, the drawdown simulated by Hantush-Jacob equation was less than that evaluated by the new theory which considered the bending effect of confining unit. The relative errors would be remarkable in the beginning of pumping and/or near the pumping well.
-
Key words:
- radial flow /
- bending /
- confined aquifer /
- leaky /
- analytical solution
-
0. 引言
对承压含水层在人类开采作用下地下水的非稳定流动, 自1935年著名的Theis公式[1]被提出以来, 传统的地下水渗流理论对之进行了近70年的分析研究, 建立了一系列对应各种条件的承压含水层井流解析模型.这些模型为解释承压含水层井流现象、分析抽水试验数据、辩识含水层参数乃至地下水资源的管理提供了重要的理论工具, 已经发挥了巨大的作用.
然而, 对于实际观测到的地下水渗流-含水介质变形的一些耦合现象, 包括承压含水层非稳定井流和盖层弯曲的相互作用, 这些传统的理论模型还无法解释, 尽管这些现象有时看起来是微弱的、难以觉察的.随着人类观测技术水平的不断提高和对地质变化敏感度的加强, 这种发生在含水层体系中的渗流-变形耦合现象也越来越得到关注.为了解释这些现象, 需要从理论上突破传统承压含水层模型的一些不合理假设.例如: 为了解释所谓的“Noordbergum效应” (在承压含水层抽水时, 上部或下部的弱透水层发生快速的小幅度的水头上升现象), Hsieh[2]、Kim和Parizek[3]利用Boit固结理论分析这些弱透水层的水头波动与含水介质变形的关系, 并进行了有限元计算; 为了解释循环抽水试验中的滞后效应, Burbey[4]应用非线性的应力-应变有限元模型考察含水层压缩与水头变化的响应特征.就含水层的变形行为, Burbey[5]还对传统地下水理论中只考虑垂向变形的做法提出质疑, 他通过数值分析认为, 在抽水条件下有多达50%的地下水是通过含水层的横向变形释放的.
陈崇希和吴修义[6]在分析一个无越流承压含水层的抽水试验时发现, 抽水初期(50 min内) 水头降深显著大于用Theis公式计算的结果.“显著”是指具有可观测性, 在抽水井径距r=104 m, 观测孔的最大偏差超过3 cm, 显然随径距r的减小偏差值会增大.他们提出, 这种现象的一个重要原因是含水层顶板发生弯曲, 起到了“梁”的作用, 抵消了部分荷载, 从而使水头降深超过Theis公式的估计值.王旭升和陈崇希[7]采用有效应力原理进一步分析了无越流承压含水层井流-盖层弯曲效应的机制, 通过引入弹性薄板理论, 建立了初步的解析模型来探讨顶板弯曲可能对无越流承压含水层井流造成的影响, 证明Theis公式计算的抽水降深是偏小的.然而, 这一改进模型忽略了水的压缩性, 也没有考虑越流, 需要加以完善.
笔者认为, 承压含水层井流-盖层弯曲效应是不同于上述Noordbergum效应和滞后效应的一种含水层变形-地下水渗流耦合作用, 后两者发生在未固结或弱固结的含水层体系(如第四系含水层), 而前者不仅会发生在未固结或弱固结的含水层体系中, 还会发生在已固结的基岩含水层体系中, 需要不同于Biot固结模型的理论加以解释.本文之目的, 就是建立一个相对较完善的解析理论, 用于分析无越流和有越流的承压含水层井流-盖层弯曲效应(以下简称井流-弯曲效应).
1. 应力分析
根据有效应力原理, 承压含水层总应力σ、有效应力σ′和孔隙水压力p之间的关系为[8]
(1) 因此增量关系为
(2) 当在含水层抽水时, 含水层孔隙水压力变化与水头降深s存在对应关系
(3) 其中, γw为水的容重.有效应力变化与含水层的压缩量存在对应关系
(4) 其中, w为承压含水层的压缩量, 即顶板垂直向下的弯曲挠度, α是含水层骨架的压缩系数, M为承压含水层的厚度.
文献[7]已经推导出, 假定含水层底板不变形, 在单位水平面积的含水层柱体中由于水头降深(水膨胀) 和有效应力增大(骨架压缩) 导致的水体积变化ΔV为
(5) 其中, n是含水层的孔隙度, β是水的压缩系数.
传统的地下水理论假定承压含水层的总应力不随抽水过程变化, 因此Δσ′=γws.用ΔV′表示这种假定条件下单位面积的释水量, 则有
(6) 其中
(7) 本文将μm称为含水层骨架压缩给水度, 将μw称为地下水膨胀给水度, 两者与我们所熟知的承压含水层弹性给水度μe的关系为
(8) 因此, 传统的承压含水层给水度概念, 是建立在假定总应力不变这一基础上的.
本文考虑承压含水层顶板的弯曲, 因此不再假定总应力守恒, 含水层单位面积的释水量应该为ΔV.根据(2) 式有
(9) 把(9) 式和(6) 式代入(5) 式, 得到
(10) 由于含水层顶板弯曲产生支持力, 抵消了一部分铅直荷载, 导致总应力下降, 有Δσ < 0, 从而ΔV < ΔV′.这说明在相同的降深条件下, 受承压含水层顶板弯曲的影响, 地下水的释放量小于传统理论的估计.因此, 为了保持水均衡, 在抽水井附近就会产生更大的抽水降深.
把(3)、(4)、(7) 式代入(2) 式, 得到总应力变化的表达式
(11) 因此总应力变化是由承压含水层的抽水降深和顶板的弯曲挠度同时决定的.
上述应力分析表明, 井流-弯曲效应的实质是承压含水层盖层弯曲导致含水层总应力下降, 诱发比传统理论估计更大的抽水引起的水头降深.
2. 无越流承压含水层的解析模型
考虑一无越流的均质各向同性承压含水层, 水平无限延伸, 有一口完整井抽水, 抽水流量恒定为Q, 如图 1所示.在水平面上以井心为原点, 建立轴对称解析模型.同时, 假定顶板的弯曲符合弹性薄板理论.
图 1 无越流承压含水层-井孔模型概化图(箭头表示水流方向)Fig. 1. Schematic for a fully confined aquifer-well system2.1 数学模型及解析解
承压含水层中地下水的径向流方程为
(12) 其中, ∂(ΔV)/∂t是单位面积含水层柱体内水体积(贮水量) 的变化率, T为导水系数, q (r, t) 为源汇项, r表示径向距离, t表示时间.在本文中, 假定顶板的挠度(即含水层的压缩量) 较小, 从而导水系数T的变化可以忽略.
把(4)、(5) 两式代入上式, 得到
(13) 在此, 承压含水层总应力的减少量就是导致盖层(顶板) 发生弯曲的附加荷载, 根据弹性薄板理论[9], 挠曲方程为
(14) 其中D为挠曲刚度,
(15) 式中E、v、b分别为顶板的弹性模量、泊松比和厚度.
(13) 和(14) 式为无越流承压含水层井流-弯曲效应的控制方程.此外, 这一问题的初始条件为
(16) 边界条件分别为
(17) 
(18) 
(19) 
(20) 其中(17) 式反映的是抽水井条件, rw为抽水井的有效半径.
方程(13)、(14) 和(16) ~ (20) 共同构成了无越流承压含水层井流-弯曲效应的数学模型.利用Hankel变换和逆变换可以求出该问题的解析解为
(21) 
(22) 其中
(23) 
(24) 而J0 (x) 是一类零阶Bessel函数.
通过适当变换, 降深的解析解可以表示为无量纲的形式
(25) 其中M为一积分函数
(26) 而无量纲因子分别为
(27) 
(28) 在以下3种情况下, 该降深解析解退化为Theis公式
(29) 
(30) 
(31) 其中W是Theis井函数.这3种情况的物理意义分别为: 公式(29), 含水层顶板挠曲刚度为无穷大, D=∞, 即组成顶板的物质极端坚硬; 公式(30), 含水层顶板挠曲刚度为零, D=0, 即组成顶板的物质极端柔软; 公式(31), 含水层骨架不可压缩, 其弹性给水度等于地下水的膨胀给水度.
2.2 对比分析
新的降深解析解表明, 在井流-弯曲效应中, 水头降深受到3个综合参数的控制: a、c和φ.其中: a是Theis公式中原有的参数, 取决于承压含水层的水文地质性质; c和φ是考虑井流-弯曲效应引入的新参数, c反映了顶板抗弯曲的性能, 而φ=μw/μe反映了地下水本身的膨胀对含水层释水的贡献.
图 2给出了井流-弯曲效应下无量纲降深sD随无量纲时间tD的变化曲线, Theis解对应φ=1的情况, 即承压含水层骨架不可压缩, 抽水量完全由地下水的膨胀所提供, 显然这是一种极端的情况.图 2表明, Theis公式估计的抽水降深是偏小的, 偏小的程度在抽水初期可能十分显著(相对误差很大), 随着时间的延长, 新模型的解析解与Theis解接近.地下水膨胀给水度μw占含水层弹性给水度μe的比例越小, 抽水初期Theis解偏小的程度就越大.更多的对比计算可以发现, 井流-弯曲效应形成与Theis公式偏差的幅度, 在抽水井附近是较显著的, 随着离抽水井距离的增大, 偏差呈现减小趋势.
图 2 当rD=0.1时, 无越流承压含水层单井定流量抽水的sD-tD曲线Fig. 2. sD-tD curve for the fully confined aquifer-well systems while rD=0.13. 一类越流承压含水层的解析模型
关于一类越流系统的水文地质特征, 见文献[10].本文假定承压含水层底板为不可变形的基岩, 含水层水平无限延伸、均质各向同性.有一完整井在承压含水层中抽水, 流量恒定为Q, 上部潜水含水层中的地下水通过弱透水层向下越流, 但是潜水水位保持不变, 示意图见图 3.假定由弱透水层和潜水含水层组合构成的承压含水层盖层符合以弹性薄板理论为基础的经典线性叠层板(复合材料) 理论, 不考虑弱透水层本身的压密释水, 建立井流-盖层弯曲效应的轴对称分析模型.
3.1 数学模型及解析解
有越流承压含水层地下水径向流方程为
(32) 其中L′=k/m为越流系数, k、m分别为弱透水层的垂向渗透系数和厚度.
在盖层弯曲方面, 一类越流承压含水层与无越流承压含水层相同, 即总应力的减少量就是导致盖层发生弯曲的附加荷载, 挠曲方程保持(14) 式不变.根据经典线性叠层板理论[11], 盖层挠曲刚度是潜水含水层挠曲刚度与弱透水层挠曲刚度的组合, 组合公式在此不赘述.
模型的初始条件和边界条件仍然用(16) ~ (20) 式描述.
因此, 方程(32)、(14) 和(16) ~ (20) 共同构成了一类越流承压含水层井流-弯曲效应的数学模型.同样利用Hankel变换和逆变换可以得到该问题的解析解
(33) 
(34) 其中
(35) 
(36) 而a、c的定义与(24) 式相同, φ的定义见(28) 式.
容易看出, 当L=0, 即弱透水层完全不透水时, 一类越流承压含水层降深和盖层弯曲挠度的解析解退化为无越流承压含水层条件下的解析解.
对于一类越流承压含水层中的非稳定井流, Hantush和Jacob[12]给出了传统理论解, 其无量纲形式为
(37) 其中
(38) 
(39) 根据(34) 式, 在井流-弯曲效应作用下, 一类越流承压含水层单井定流量抽水引起的无量纲降深sD可以表示为以下的井函数
(40) 其中
(41) 3.2 对比分析
与无越流承压含水层井流-弯曲效应下水头降深的无量纲井函数(26) 式相比, 一类越流承压含水层的无量纲降深井函数(41) 式多了一个综合参数B.这一参数反映了弱透水层的越流能力.B越小, 说明通过相邻含水层产生的越流越强烈, 对被开采的承压含水层地下水径向流的影响就越大.参数B已经包含在传统理论解(37) 式中.
现取一组无量纲因子rD=0.1, φ=0, r/B=0.5, 分别采用Theis公式、Hantush-Jacob公式(37)、无越流条件的井流-弯曲效应公式(26) 和一类越流条件的井流-弯曲效应公式(41) 计算无量纲降深sD随无量纲时间tD的变化.计算结果见图 4.
图 4 当rD=0.1, φ=0, r/B=0.5时, 一类越流承压含水层单井抽水的sD-tD曲线Fig. 4. sD-tD curve for the leaky aquifer-well systems while rD=0.1, φ=0 and r/B=0.5图 4表明有越流的条件下, 开采层的水头降深在抽水初期与无越流条件较为接近, 但随着时间的延长, 其降深值越来越明显的小于无越流条件, 即相邻含水层越流所补充的地下水占抽水量的比例越来越大.Hantush-Jacob公式所估计的水头降深, 也小于有越流条件下井流-弯曲效应的降深值, 随时间延长, 两者都向同一个固定的降深值逼近.这说明盖层的弯曲并不影响有越流承压含水层在达到稳定流时的水头分布.
4. 结论
承压含水层井流-盖层弯曲效应是一种特殊的含水层变形-地下水渗流耦合作用, 没有被传统的地下水动力学理论所认识到.通过应力分析表明, 承压含水层井流-盖层弯曲效应的机制是在开采井抽水条件下, 承压含水层盖层发生弯曲导致含水层总应力下降, 从而诱发比传统理论估计更大的抽水降深.
通过引入弹性薄板理论, 本文建立了无越流和有越流承压含水层井流-盖层弯曲效应的解析模型, 得到2个新的井函数.考虑井流-盖层弯曲效应时, 对无越流承压含水层来说, Theis公式计算的水头降深是偏小的, 对一类越流承压含水层来说, Hantush-Jacob公式计算的降深是偏小的.在有越流条件下, 井流-盖层弯曲效应并不影响最终稳定流所对应的水头分布.无量纲降深的对比分析表明, 传统理论由于不考虑井流-盖层弯曲效应, 在抽水井附近、抽水初期的降深计算可能产生显著的相对误差.
-
图 1 无越流承压含水层-井孔模型概化图(箭头表示水流方向)
Fig. 1. Schematic for a fully confined aquifer-well system
图 2 当rD=0.1时, 无越流承压含水层单井定流量抽水的sD-tD曲线
Fig. 2. sD-tD curve for the fully confined aquifer-well systems while rD=0.1
-
[1] Theis C V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground water storage[J]. Trans Ame Geophys, 1935, 16: 519-524. doi: 10.1029/TR016i002p00519 [2] Hsieh P A. Deformation-induced changes in hydraulic head during ground-water withdrawal[J]. Ground Water, 1996, 35(6): 1082-1089. [3] Kim J M, Parizek R R. Numerical simulation of the Noord-bergum effect resulting from groundwater pumping in a layered aquifer system[J]. Journal of Hydrology, 1997, 202(1-4): 231-243. doi: 10.1016/S0022-1694(97)00067-X [4] Burbey T J. Modeling three-dimensional deformation in response to pumping of unconsolidated aquifers[J]. Environmental & Engineering Geosciences, 1999, 5(2): 199-212. [5] Burbey TJ. Stress-strain analyses for aquifer-system characterization[J]. Ground Water, 2001, 39(1): 128-136. doi: 10.1111/j.1745-6584.2001.tb00358.x [6] 陈崇希, 吴修义. 边界附近地下水不稳定井流试验数据的分析法[A]. 综合治理和利用矿床大面积地下水经验汇编[C]. 北京: 煤炭工业出版社, 1979. 22-41.CHEN C X, WU X Y. Analytical methods for pumping tests near boundary[A]. Experiences of controlling and utilizing groundwater in large areas[C]. Beijing: Coal Industry Press, 1979. 22-41. [7] 王旭升, 陈崇希. 改进的Theis井流模型及其解析解———虑含水层顶板的挠曲作用[J]. 地球科学———中国地质大学学报, 2002, 27(2): 199-202. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200202018.htmWANG X S, CHEN C X. Analysis of modified Theis model on well flow: Considering bending of the confining stratum [J]. Earth Science—Journal of China University of Geosciences, 2002, 27(2): 199-202. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200202018.htm [8] Bear J. Dynamics of fluids in porous media[M]. New York: Amer Elsevier Publishing Company, 1972. [9] Arthur P B, Omar M S. Advanced mechanics of materials [M]. New York: John Wiley & Sons Inc, 1985. [10] 陈崇希. 地下水不稳定井流计算方法[M]. 北京: 地质出版社, 1983.CHEN C X. Analytical methods of transient groundwater flow toward wells[M]. Beijing: Geological Publishing House, 1983. [11] 沈观林. 复合材料力学[M]. 北京: 清华大学出版社, 1996.SHEN G L. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 1996. [12] Hantush M S, Jacob C E. Non-steady radial flow in an infinite leaky aquifer[J]. Trans Amer Geophys, 1955, Union 36: 95-100. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 3817
- HTML全文浏览量: 437
- PDF下载量: 12
- 被引次数: 0
