FINITE ELEMENT METHOD FOR MODELING RESISTIVITY SOUNDING ON 3-D GEOELECTRIC SECTION
-
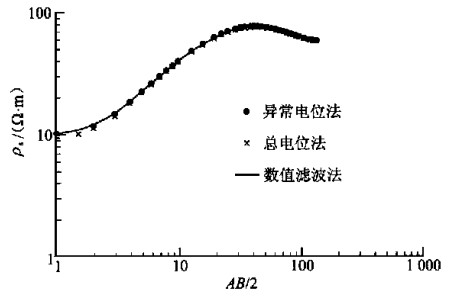
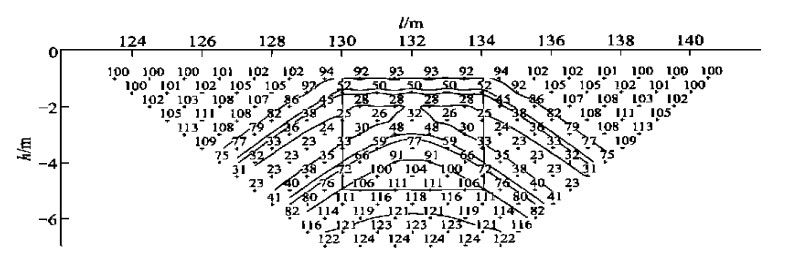
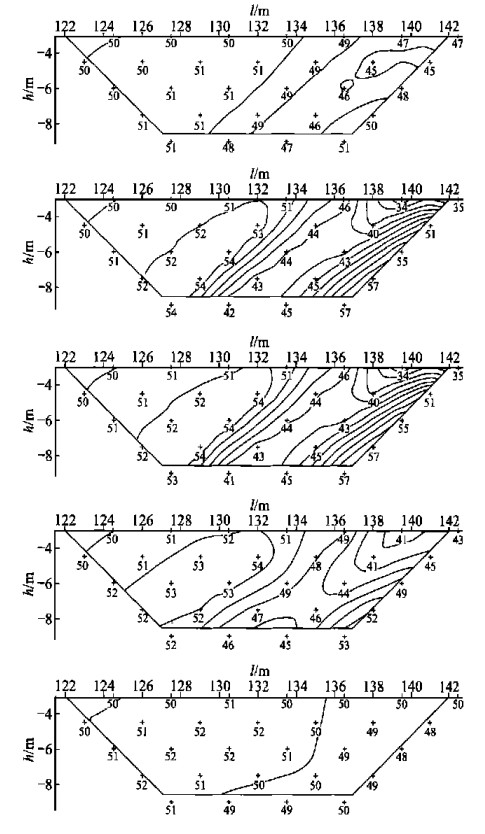
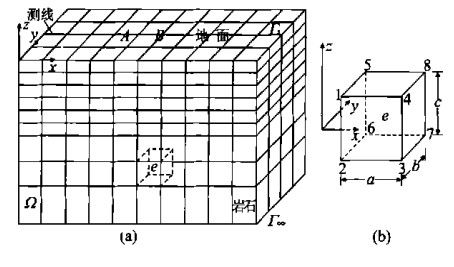
摘要: 用有限单元法进行了电导率分块均匀的三维点源电场电阻率测深的数值模拟.首先给出了三维构造中点源电场的边值问题、变分问题; 然后, 用有限单元法求解变分问题, 将区域剖分成六面体单元, 在单元中进行三线性函数插值, 将变分方程化为线性代数方程组; 最后解方程组, 得各节点的电位值, 进而计算出地表的视电阻率.对几例较典型的地电模型进行试算, 结果表明本方法是行之有效的Abstract: The finite element method is used for the numerical modeling of the resistivity sounding in a 3-D point-source electric field whose conductivities are homogeneous for each block. In this paper, the 3-D boundary value and variational equation concerning the point-source electrical field in the 3-D structure are both presented. Then the finite element method is used to solve the variational equation. The entire region is divided into many hexahedral units in each of which a trilinear function is interpolated. The variational equation is converted into a linear equation system. Finally the equation system is solved to obtain the potential value on each of the nodes, resulting in the calculation of the apparent resistivity on the ground surface. The test of several relatively typical geoelectric models shows that this finite element method is effective.
-
有限元法求解三维电场数值模拟理论问题国内外[1~3]都曾做过这方面的工作, 但是由于当时计算机内存和速度的限制, 使得研究工作没能发展到实用编程计算阶段.近年来, 计算机计算速度和内存比过去大为提高, 使得我们能够将三维有限元数值模拟进入实用阶段.本文将介绍三维地电断面电阻率测深有限元数值模拟技术, 主要包括: 三维电阻率测深电场的边值问题和变分问题, 六面体网格、电位三线性插值有限元数值模拟方法, 边界单元的处理, 以及几例典型模型的计算.
1. 边值问题
三维地电断面双点电源总电位及异常电位的边值问题可归纳为[3, 4]:
(1) 总电位v.
(1) (2) 异常电位u.
(2) 式中: Γs为区域Ω的地面边界, Γ∞为区域Ω的地下边界, n为边界的外法向方向, σ为介质的电导率, σ′=σ-σ0为介质的异常电导率, σ0为电源点处电导率, u0为正常电位, 它等于
(3) 其中, rA, rB分别是测点至电源点A, B的距离.
2. 变分问题
与上述三维电场的边值问题(1), (2) 等价的变分问题分别为
(4) 
(5) 3. 有限单元法
变分问题(4) 和(5) 的求解可用有限单元法, 这里给出解变分问题(5) 的步骤如下:
① 用六面体单元对区域Ω进行剖分, 参见图 1a.将方程(5) 中对区域Ω和边界Γ∞的积分分解为对各单元e和Γe的积分之和:
(6) ② 单元中电位采用三线性插值, 即
(7) 式中: Ni (i=1, 2, …, 8) 为形函数, 等于[3]
(8) 其中, ξi, ηi, ζi是点i的坐标; ξ, η, ζ与x, y, z的关系为
(9) x0, y0, z0是子单元的中点, a, b, c是子单元的3个边长.将(7) 至(9) 式代入方程(6), 得:
方程(6) 第一项单元积分
(10) 其中: K1e= (k1ij), k1ij=k1ji, ue= (ui)T, i, j=1, 2, …, 8.
由(8) 式, 可得的k1ij具体计算公式如下:
其中,
方程(6) 第二项单元积分
(11) 其中, u0e= (u0i)T, i=1, 2, …, 8.
方程(6) 中最后两项积分是对Γ∞的边界积分, 若单元e的一个面1234(参见图 1b) 落在无穷远边界上, 由于无穷远边界离电源较远, 可将
(12) 看作常数, 提至积分号之外, 所以方程(6) 第三项边界面积分
(13) 其中:
同样, 方程(6) 第四项边界面积分
(14) ③ 在单元内, 将(10), (11), (13), (14) 式的积分结果相加, 再扩展成由全体节点组成的矩阵或列阵:
其中: Ke=σ (K1e+K2e), K′e=σ′ (K1e+K2e); u, u0分别是全体节点u, u0组成的列向量; Κe‚Κ'e分别是Ke, K′e的扩展矩阵.
由全部单元的Fe (u) 相加, 得
(15) 令式(15) 的变分为零, 得线性方程组
(16) 解上述方程组, 得各节点的u.之后, 便可按下式计算视电阻率
(17) 式中: K为装置系数; u (M), u (N) 分别是测量电极M, N所在节点的电位值; ρ0为电源点处电阻率.
4. 算例
(1) 模型一为3层水平层状大地, 层参数为: 第一层厚度为2 m, 电阻率为10 Ω·m; 第二层厚度为10 m, 电阻率为200 Ω·m; 第三层电阻率为50 Ω·m.从图 2中可见, 异常电位法得到的测深曲线与数值滤波法所得的测深曲线完全拟合, 而总电位法得到的测深曲线在首支由于电源点影响而与数值滤波法所得的测深曲线有所差异, 反映本文导出的有限元模拟方法计算精度是可靠的.
图 2 有限元法与数值滤波法结果对比Fig. 2. Comparison of numerical filter wave and finite element method numerical solutions(2) 模型二为地下有一4m×4 m×4 m的低阻方形矿体, 其电阻率为5 Ω·m, 顶部埋深为1 m, 围岩电阻率为100 Ω·m.它的偶极-偶极排列中心剖面的视电阻率等值线计算结果见图 3所示.其中极距AB=MN=1 m, 有限元区域网格剖分为52×28×14个单元, 在Pentium Ⅲ 550 Hz计算机计算时间为14 669 s.该正演结果显示与模型实验结果极为相似.
图 3 模型2偶极-偶极视电阻率等值线(单位: Ω·m)Fig. 3. Dipole-dipole apparent resistivity contour of model 2(3) 模型三如图 4所示, 水平地形下含有2个体积大小、电阻率均不相同的方形矿体.矿体1的体积为4 m×4 m×4 m, 电阻率为100 Ω·m, 顶部埋深为3 m; 矿体2的体积为3 m×3 m×3 m, 电阻率为10 Ω·m, 顶部埋深为1 m.两矿体横向间距7 m, 围岩电阻率为50 Ω·m.图 5为沿y方向的5个断面的视电率等值线, 极距AB=MN=3 m.
-
图 2 有限元法与数值滤波法结果对比
Fig. 2. Comparison of numerical filter wave and finite element method numerical solutions
图 3 模型2偶极-偶极视电阻率等值线(单位: Ω·m)
Fig. 3. Dipole-dipole apparent resistivity contour of model 2
-
[1] Pridmore D F, HohmanG W, Ward S H, et al. An investigation of finite elementmodeling for electrical and electromagnetic data in three dimensions[J]. Geophysics, 1981, 46: 1009~ 1024. doi: 10.1190/1.1441239 [2] Holcombe HT, JiracekG R. Three-dimensional terrain correction in resistivity surveys[J]. Geophysics, 1984, 49(4): 436 ~ 452. doi: 10.1190/1.1441679 [3] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994. 178~ 183. [4] 罗延钟, 张桂青. 电子计算机在电法勘探中的应用[M]. 武汉: 武汉地质学院出版社, 1987. 67~ 69. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 3705
- HTML全文浏览量: 471
- PDF下载量: 28
- 被引次数: 0
