CSD SOFTWARE DESIGN FOR FINITE-STRAIN DETERMINATION WITH INVERSE SURFOR WHEEL
-
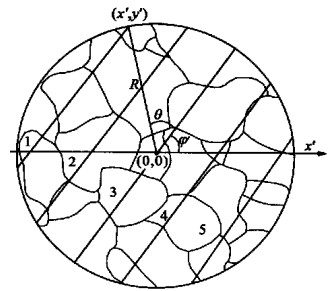
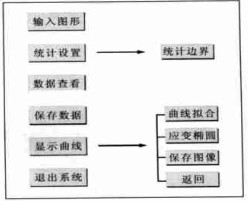
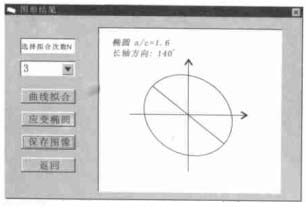
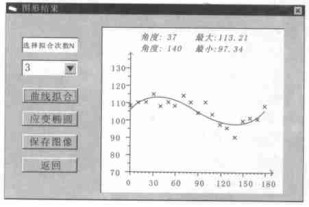
摘要: 用计算机实现反向轮法测岩石有限应变的过程, 可提高有限应变测量的准确性和效率.开发出了用Visual Basic 5.0编写的CSD软件, 利用岩石薄片图像或者矿物颗粒轮廓图测出岩石有限应变的大小及应变椭圆长轴方向, 同时测出矿物颗粒分布的优选方位.其操作相当简便, 首先统计出图像中0°~180°各方向上矿物颗粒的边界数目; 然后在方位-边界坐标系中投点, 并利用最小二乘法进行数据点的多项式曲线拟合; 最后求出曲线的极值点坐标, 并根据坐标绘制相应的应变椭圆.软件运行中, 统计出的边界数据和拟合曲线以及应变椭圆图形都是可视的, 并能进行相应的保存.Abstract: Computer simulation of finite-strain determination with the inverse SURFOR wheel may improve the preciseness and efficiency of the strain determination. The CSD softwre, programmed in Visual Basic 5.0 and very simple for its friendly interface, can be used to measure the size of the finite strain and the direction of the long axis of the finite strain ellipse in deformed rocks by means of section images or mineral grain sketches. At the same time, this software can also be used to measure the preferred orientation of the mineral grain distribution. Firstly, the CSD software collects boundaries of mineral grains in the image at all directions from 0°-180°. Secondly, the boundary data dots are distributed in the orientation-boundary coordinate system, and the polynomial curve fitting is made by means of the least-squares. Lastly, the extreme point coordinate of the fitted curve is obtained, and the corresponding strain ellipse is drawn up in line with the coordinate. During the operation of the CSD software, all the collected data of mineral grain boundaries and the resulting fitted curve, and the strain ellipse images can be both visible and saved in the corresponding files.
-
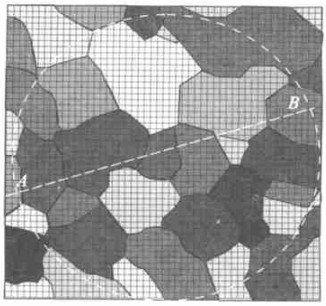
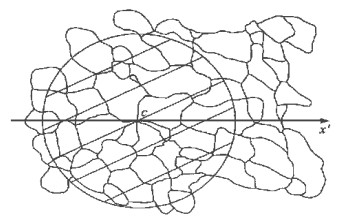
图 6 砂岩矿物颗粒轮廓图(a)及手工拟合曲线(b)[3]
Fig. 6. Outlines of grain boundaries in a quartzite and its curve fitted by hand
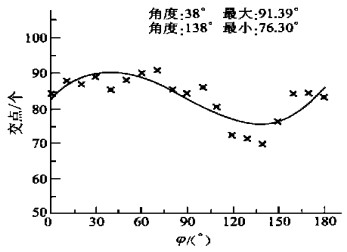
表 1 CSD软件统计出的边界数据和方向
Table 1. The boundary data and orientation collected by the software CSD

-
[1] Ghaleb A R, Fry N. CSTRAIN: A Fortran77 program to study Fry' s plots in two-dimensional simulated models[ J]. Computers & Geosciences, 1995, 21(7): 825~831. [2] Allard B, Benn K. Shape preferred-orientaition analysis using digitized images on a microcomputer[ J]. Computers & Geosciences, 1989, 15(3): 441~448. [3] Panozzo R. Two-dimensional strain determination by the inverse SURFOR wheel[ J]. Journal of Structural Geology, 1987, 9(1): 115~119. doi: 10.1016/0191-8141(87)90049-6 [4] GoodchildJ S, Fueten F. Edge detection in petrographic images using the rotating polarizer stage[ J]. Computers & Geosciences, 1998, 24(8): 745~751. [5] Knappertsbusch M W. A simple Fortran77 program for outline detection[ J]. Computers & Geosciences, 1998, 24(9): 897~900. [6] 刘振安, 苏仕华. C语言图形设计[M]. 北京: 人民出版社, 1995.16~18. [7] Hart D, Rudman A J. Least-squres fit of an ellipse to anisotropic polar data: application to azimuthal resistivity surveys in karst regions[ J]. Computers & Geosciences, 1997, 23(2): 189~194. [8] Thompson G T, Balch S J. An efficient algorithm for polynomial curve fitting[ J]. Computers & Geosciences, 1988, 14(5): 547~556. -









 下载:
下载: