NUMERICAL SIMULATION OF POLLUTANT MIGRATION IN MULTI-LAYER MEDIA WATER-BEARING SYSTEM CONTAINING AQUITARD: A CASE STUDY OF TIEBUTIE POOL, DAQING CITY
-
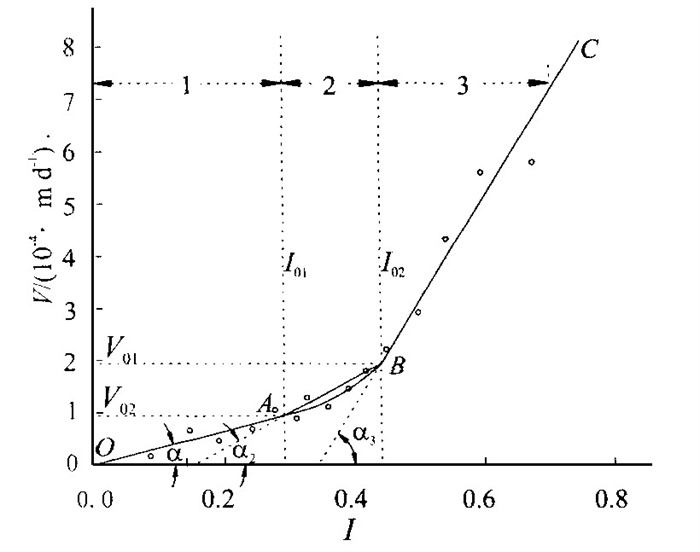
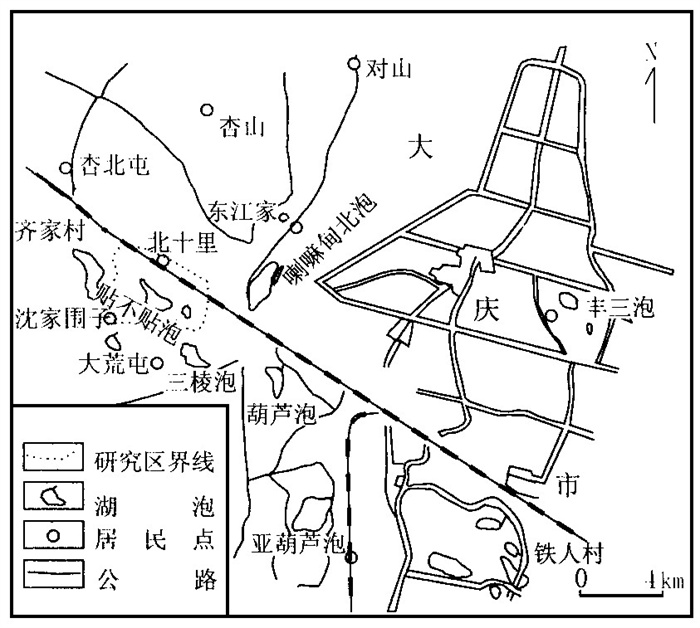
摘要: 选取大庆市贴不贴泡区具有普遍意义的饱和-非饱和多层介质含水系统中石油类污染为研究对象.在分析水文地质条件的基础上, 利用实验研究获得含水系统中连接上下含水层的弱透水层的渗透规律, 然后运用数值模拟技术建立起此类含水系统中石油类污染质运移数值模拟模型.应用所建模型对污染质的污染趋势进行了预测, 并提出污染控制措施.Abstract: The typical oil pollution in the saturated-unsaturated multi-layer media water-bearing system characteristic of Tiebutie Pool in Daqing City is chosen as the object of the present investigation. On the base of the analysis of the hydrogeological data, the permeability law of the aquitard linking the upper and lower water-bearing beds in the water-bearing system has been achieved by an experimental research. Then the numerical simulation model of the oil pollutant migration in this kind of water-bearing system is constructed by means of the numerical simulation technology. The numerical model thus established can be used to forecast the pollution trend of the pollutants and to propose the corresponding measures to control the pollution. In summary, this research result is of wide application in China where the sustainable development strategy is strongly upheld.
-
Key words:
- aquitard /
- multilayer media /
- waterbearing system /
- numerical simulation /
- pollution
-
图 2 饱和粘性土中渗透速度与水力梯度关系曲线
Fig. 2. V-I curve of the water filtration in saturated clay soil
表 1 模型参数
Table 1. Parameters in the numerical model
-
[1] 张忠胤. 关于结合水动力学问题[M ]. 北京: 地质出版社, 1980. [2] 宿青山, 刘丽, 邱枚大, 等. 现代实验水文地质[M ]. 长春: 吉林科学技术出版社, 1991. [3] 陈崇希, 唐仲华. 地下水流动问题数值方法[M ]. 武汉: 中国地质大学出版社, 1990.157～182. [4] 孙讷正. 地下水流的数学模型和数值方法[M ]. 北京: 地质出版社, 1981.214- 241. [5] 孙讷正. 地下水污染: 数学模型和数值方法[M ]. 北京: 地质出版社, 1989.123～261. -
下载:
点击查看大图
图(2) / 表(1)
计量
- 文章访问数: 3773
- HTML全文浏览量: 539
- PDF下载量: 9
- 被引次数: 0
