GEOSTATISTICAL STUDY OF w(Au)/w(Ag) ANOMALY IN GUILAIZHUANG GOLD DEPOSIT
-
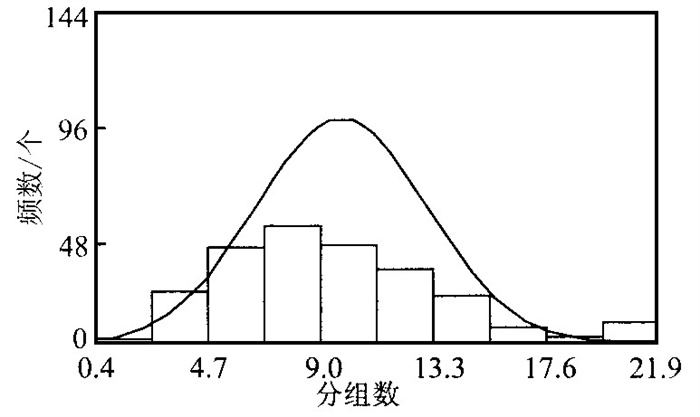
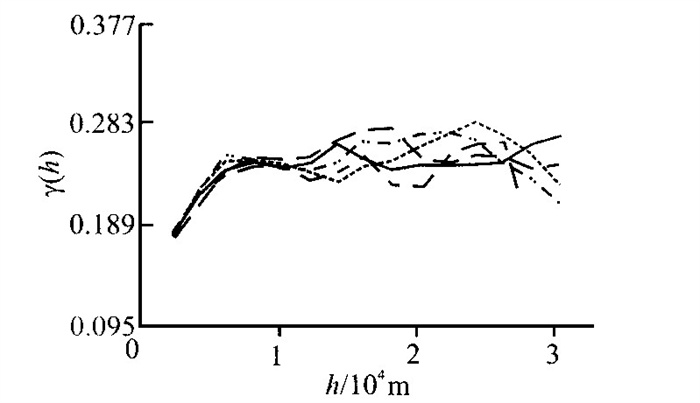
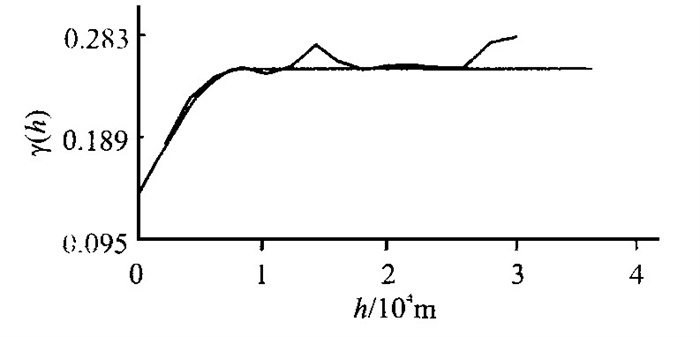
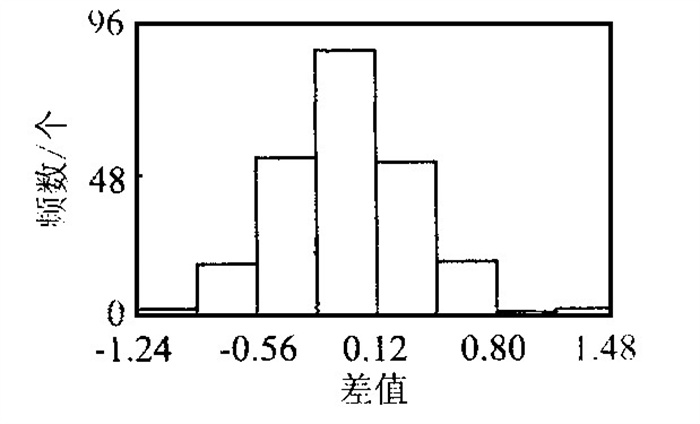
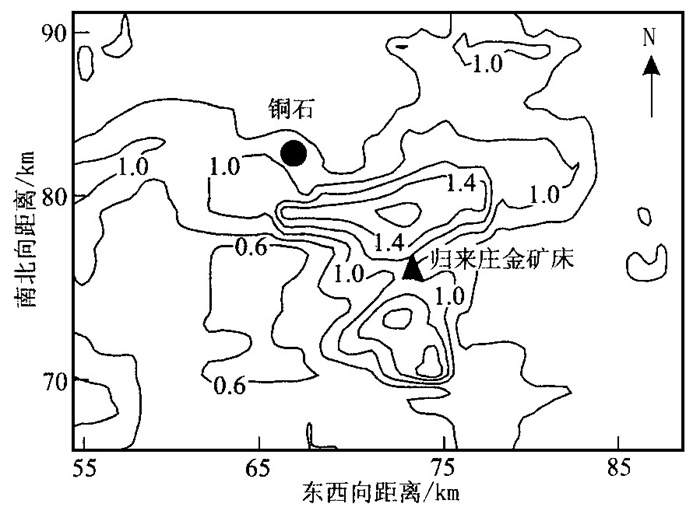
摘要: w (Au) /w (Ag) 比值在金矿床评价方面是一个重要的标志, 也可以提供金矿成因的重要信息.对归来庄金矿床的w (Au) /w (Ag) 异常进行地质统计学研究, 利用指示克立格法研究w (Au) /w (Ag) 的分布规律, 查明Au的赋存部位, 并对该区今后工作提出建议.
-
关键词:
- w(Au)/w(Ag)异常 /
- 金矿床评价 /
- 地质统计学 /
- 指示克立格法
Abstract: The w (Au) / w (Ag) ratio, an important indicator for the evaluation of gold deposits, may provide us with some important information on the origin of the gold deposits. This paper presents the geostatistical research into w (Au) / w (Ag) anomaly in the Guilaizhuang gold deposit. The indicator Kriging method is applied to the research into the distribution pattern of w (Au) / w (Ag) ratio and to the location of Au occurrence positions. Finally this paper presents some suggestions for the future research in this gold deposit. -
归来庄金矿床产出于华北地台东部, 是与富钾碱性次火山岩浆活动紧密相关的富含贵金属的石英-萤石-冰长石型中低温热液金矿床[1].据山东省地矿局资料研究, 在铜石杂岩体范围内, Au矿化增强时, Ag, As, Sb, Mo, Bi, Hg等的含量都相应增高, 表明这些元素对金成矿具有指示意义[2~4].Ag是矿石的主要伴生成分, Ag的矿化与Au的矿化段基本对应, 与Au的富集部位相比, Ag矿化富集部位略深[5].据统计, 金矿体中w (Au) /w (Ag) 比值(Au, Ag的品位比) 由浅部至深部略呈增高的趋势, 0 m标高以上, w (Au) /w (Ag) 比值接近1, 0 m标高以下, 其值大于2.
w (Au) /w (Ag) 比值在金矿床评价方面是一个重要的标志, 它也可以提供金矿成因的重要信息[6].对归来庄金矿床的w (Au) /w (Ag) 进行地质统计学研究, 查明w (Au) /w (Ag) 对该区金成矿及其分布的影响, 对该区今后的找矿工作具有重要的指导意义[7].
1. w (Au) /w (Ag) 指标特征
据山东省地矿局资料分析, 归来庄金矿床中Au-Ag的相关性较高.在Au特低品位(< 1×10-6) 时, w (Au) /w (Ag) 之值通常小于1.Au品位增高, Ag也相应增高, 但Au的增幅较大, w (Au) /w (Ag) 常大于1.在成矿过程中成矿溶液是从w (Au) /w (Ag) 低比值向高比值方向演化.Ag在成矿较早阶段先于Au沉淀, 剩余溶液中Au的含量提高, 晚阶段生成的金矿物的成色也提高了, 自然金可能是晚阶段沉淀的.根据Ag和Au的空间变化特征分析, 矿体浅部的w (Au) /w (Ag) 比值高, 向深部减小, 深部Ag含量高于Au, Au有向浅部富集的趋势.金在较晚阶段相对富集, Au, Ag有分异, Au富集于较低温的热液中.
对归来庄金矿床的w (Au) /w (Ag) 异常进行地质统计学研究是在一定的研究区内进行的, 研究区选在归来庄金矿床及其周边共1 000多km2的范围内.对研究区内所有含有Au, Ag的点进行取样, 共有样点241个, 根据这241个样品作w (Au) /w (Ag) 比值统计分布直方图(图 1).
直方图显示为单峰曲线, 大部分样品的w (Au) /w (Ag) 比值较低, w (Au) /w (Ag) 高比值的样品突然减少, 整个直方图呈现出一个长尾巴.实验偏度与理论偏度之比: 5.75/0.62=9.27;实验峰度与理论峰度之比: 38.71/0.31=124.87.
统计结果表明原始数据严重偏离正态分布, 若用传统的参数地质统计学来研究该区的w (Au) /w (Ag), 则应对原始数据进行处理使其服从正态分布, 以满足参数地质统计学方法对数据分布的要求.经特异值处理后服从较好的正态分布(图 2), 然而参数地质统计学需要对数据分布的平稳性作出假定, 但是这种平稳或准平稳假设很难进行检验, 这就限制了参数地质统计学方法的应用[8].
图 2 w (Au) /w (Ag) 经特异处理后的直方图Fig. 2. Histogram of w (Au) /w (Ag) after disposing outliers2. 应用指示克立格法研究w (Au) /w (Ag) 异常
由于非参数地质统计学无须要求母体服从某种分布类型, 也不需满足平稳或准平稳假设, 因而可操作性强.为了利用归来庄金矿中与金成矿相关的w (Au) /w (Ag) 信息来研究金异常, 在非参数地质统计学理论指导下, 利用指示克立格法对归来庄金矿w (Au) /w (Ag) 分布进行估计[9~11].
2.1 临界值的选择与指示转换
临界值的选择对指示克立格法来说相当关键, 它将影响到序次相关问题的出现及结构分析的正确性, 最终影响指示克立格法的估计精度[12].
据前面统计分析结果, 数据变化范围在(0.036, 10.925) 内, 均值为1.14, 94.61%的数据集中在(0.0, 2.2) 以内.经特异值处理后, 数据主要落在(0.036, 2.220) 内, 均值为0.990.在选择临界值时, 考虑到数据分布的特点, 选择了13个临界值, 且临界值主要分布在数据集中区.这13个临界值依次为: 0.10, 0.44, 0.64, 0.84, 1.03, 1.24, 1.44, 1.64, 1.84, 2.04, 2.24, 3.00, 4.00.各待估点信息样指示值的获得就是以这13个临界值作为阀值, 对不同的滑动邻域内的信息样进行指示转换.
区域化变量w (Au) /w (Ag) 连续分布, 故指示转换的表达式为:
这里Z(xa)是信息样, a= 1, …, 241;zl是临界值, l= 1, …, 13.
2.2 空间结构分析
地质统计学就是要研究那些在空间分布上既具随机性又有结构性的自然现象, 因而对区域化变量(w (Au) /w (Ag)) 进行准确的结构分析对地质统计学研究来说相当重要.区域化变量空间分布特征分析主要是通过计算其在不同方向的变异函数, 并对反映空间结构的变异函数实验曲线进行拟合来实现.
由于原始数据来自于小比例尺(1∶200 000), 数据较少, 使结构分析的精确性受到影响, 但已有的241个信息点均匀分布, 能基本反映w (Au) /w (Ag) 在该区的空间分布特征, 原则上已满足结构分析对信息样品的要求, 可以进行结构分析.
w (Au) /w (Ag) 的指示克立格法研究是以其指示转换值为基础, 计算w (Au) /w (Ag) 指示转换值在不同方向的变异函数, 绘制5个方向w (Au) /w (Ag) 经指示转换后的变异函数实验曲线(图 3).从多方向变异函数实验曲线可以看出, 5个方向的变异函数实验曲线基本一致, w (Au) /w (Ag) 在不同方向上可以认为保持各向同性.
图 3 所有5个方向w (Au) /w (Ag) 变异实验曲线Fig. 3. Semivariogram experimental curves in five directions对w (Au) /w (Ag) 的套合结构进行分析其实就是一个结合金矿成矿过程对w (Au) /w (Ag) 空间变异实验曲线的拟合过程, 如果成矿是多期多阶段的, 那么就应用多个套合结构来反映.由于归来庄金矿床在成因上主要与次火山杂岩有关, 笔者只考虑了次火山杂岩这一主要成矿地质作用, 因而只用一个套合结构来对归来庄金矿床w (Au) /w (Ag) 的空间结构进行拟合.
以135°方向的变异函数实验曲线为代表对该区w (Au) /w (Ag) 进行空间结构分析, 结果表明, w (Au) /w (Ag) 变异函数实验曲线可以用一个块金效应为0.12个单位、基台值为0.272个单位、变程是6 500 m的球状模型来拟合, 拟合结果见图 4.块金效应的大小反映了w (Au) /w (Ag) 结构间的随机变化程度; 基台值是块金效应的2倍以上, 说明w (Au) /w (Ag) 在变程范围内具有较强的相关性, 可以用克立格法来进行估计; 变程6 500 m主要与该区铜石次火山杂岩体出露范围有关.
根据套合结构分析, 归来庄金矿床w (Au) /w (Ag) 的空间变异模型简化为:
其中: γ (h) 是区域化变量的变异函数值; h是点间距离; a是区域化变量的变程.
2.3 指示克立格法方案设计
根据w (Au) /w (Ag) 的空间结构变异特征, 考虑到该金矿床具体地质情况、原始数据间距较大等方面因素, 制定适合本区的指示克立格法方案.按照超级块段法的原则, 将研究区划分成2×2四大块, 又将其细分为90×80个待估区, 待估区大小为400 m×325 m, 搜索直径为6 500 m, 各向异性比为1.
2.4 交叉验证
临界值的选择是否恰当与区域化变量的空间变异结构分析正确与否是指示克立格法估计精确性的关键.w (Au) /w (Ag) 经指示转换后得到的空间变异结构模型参数准确性需要进行交叉验证后才知道.
以w (Au) /w (Ag) 的空间结构模型参数为基础, 对该区已有的241个样点进行指示克立格法检验, 作差值统计直方图(图 5), 据该图分析: 差值变化范围在(-1.258, 2.176) 内, 均值为-0.011 5;差值在(-0.57, 0.46) 内的占总数的82.99%, 差值的绝对值大于1的仅占3.32%;由于差值集中在小值区, 方差很小, 仅0.24, 因而用该空间变异结构模型来对归来庄金矿床w (Au) /w (Ag) 进行指示克立格法估计, 其结果是可信的.
2.5 指示克立格法估计
归来庄金矿床w (Au) /w (Ag) 指示克立格法估计分布等值线如图 6所示.根据该区Au的分布, 结合图 6可以得出: w (Au) /w (Ag) > 1.5的区域基本上就是Au的异常区, 归来庄金矿床就在此区内; w (Au) /w (Ag) 高值区与Au高值区一致; 图 6表明归来庄金矿床的西北部和南部地区有高w (Au) /w (Ag) 区, 说明该矿床的西北部和南部地区有找矿前景, 因而今后在归来庄金矿区周边开展找矿工作时, 应重点考虑其西北部和南部与次火山杂岩体接触部位.
图 6 w (Au) /w (Ag) 指示克立格法估计分布等值线Fig. 6. w (Au) /w (Ag) isoline of indicator Kriging estimation3. 结论
归来庄金矿床w (Au) /w (Ag) 的地质统计学研究结果表明, w (Au) /w (Ag) 对归来庄金矿的找金工作具有指导意义, 可以作为找矿标志.应加强金矿成矿指示元素的研究, 如Ag, As, Sb, Mo, Bi, Hg等, 加强新技术、新理论、新方法在该区的应用, 提高对现有资料的利用率, 增强多元信息的综合提取能力.今后除继续加强归来庄金矿区与铜石次火山杂岩体接触带的找矿工作外, 可以适当将找矿空间放大, 向矿区的西北部、南部和东南部展开.
-
图 2 w (Au) /w (Ag) 经特异处理后的直方图
Fig. 2. Histogram of w (Au) /w (Ag) after disposing outliers
图 3 所有5个方向w (Au) /w (Ag) 变异实验曲线
Fig. 3. Semivariogram experimental curves in five directions
-
[1] 于学峰. 归来庄金矿床的地质特征及成因[M]. 济南: 山东科学技术出版社, 1996. 129~ 139. [2] 陈永清. 鲁西综合信息金成矿系列预测理论和方法研究[D]. 长春: 长春地质学院, 1994. [3] 林景仟, 谭东娟, 于学峰, 等. 鲁西归来庄金矿成因[M]. 山东: 山东科学技术出版社, 1996. 40~ 103. [4] 林景仟, 谭东娟, 于学峰, 等. 归来庄金矿成因及成矿模式[J]. 长春地质学院学报, 1995, 25(3): 286~ 293. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ503.007.htm [5] Chen Y Q, Zhao P D. Zonation in primary halos and geo- chemical prospecting pattern for the Guilaizhuang gold de- poisit, eastern China[J]. Nonrenewable Resources, 1998, 7(1): 37~ 44. doi: 10.1007/BF02782507 [6] 赵鹏大, 池顺都, 陈永清. 查明地质异常: 成矿预测的基础[J]. 高校地质学报, 1996, 2(2): 61~ 373. https://www.cnki.com.cn/Article/CJFDTOTAL-GXDX604.000.htm [7] 赵鹏大, 陈永清. 地质异常矿体定位的基本途径[ J]. 地球科学———中国地质大学学报, 1998, 23(2): 111~ 114. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX802.000.htm [8] Murphy J. The indicator variogram and the simple Kriging estimator: useful tools to complement lithologic correlation in a complex fluvial depositional environment[ J]. AAPG Bulletin, 1995, 79(4): 594~ 599. [9] 肖斌, 赵鹏大, 侯景儒, 等. 时空域中的指示克立格理论研究[J]. 地质与勘探, 1999, 35(4): 25~ 29. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKT199904007.htm [10] 侯景儒. 指示克立格的理论与方法[ J]. 地质与勘探, 1990, 26(3): 28~ 36. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKT199003005.htm [11] 周蒂. 稳健统计学与地球化学数据的统计分析[J]. 地球科学———中国地质大学学报, 1991, 16(3): 273~ 280. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX199103007.htm [12] Carr J R, Bailey R E. Use of indicator variograms for an enhanced spatial analysis[ J]. Math Geol, 1988, (8): 797~ 812. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 4038
- HTML全文浏览量: 480
- PDF下载量: 10
- 被引次数: 0
