AN APPROACH TO TIME-SHIFTED NORMAL MOVEOUT AND STACKING
-
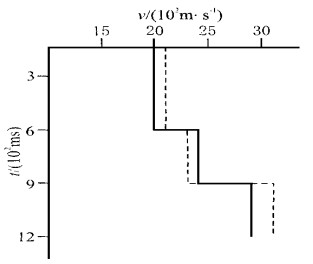
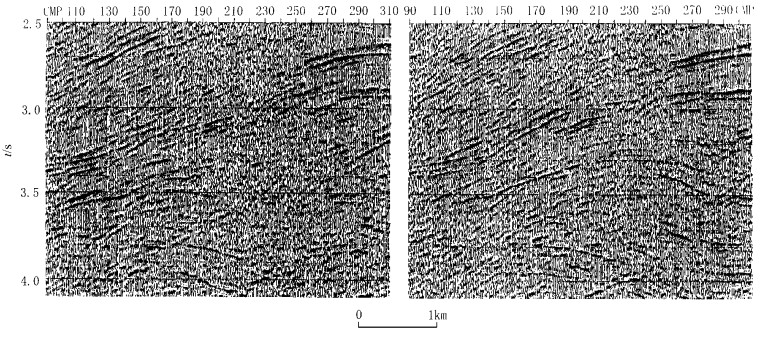
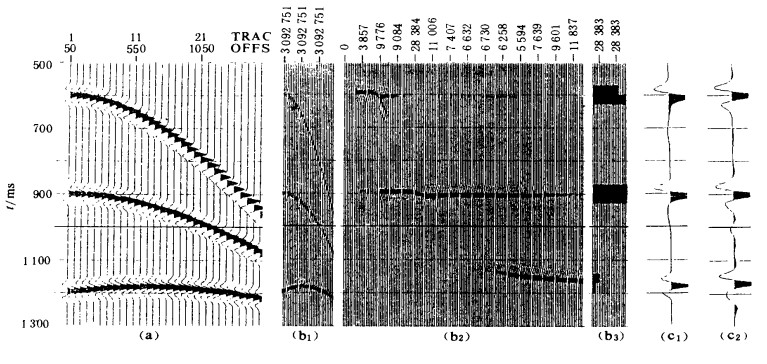
摘要: 在水平层状介质假设情况下, 推导了反射波时距曲线的表达式, 指出: 在对水平层状介质情况下, 反射波时距曲线是一时移双曲线.通过对理论模型和实际资料的处理, 表明时移动校正和叠加方法具有高保真、高分辨率和明显的叠加成像效果.同时, 用时移动校正τ0分析谱计算层速度较以往用Dix公式由叠加速度计算层速度精度要高.这种方法不仅可以用于复杂构造的地震资料的叠加成像, 也可以应用到高分辨率处理的流程中.Abstract: The expression of the time-interval curve of the reflective waves is derived on the condition of the horizontal layered strata, indicating that the time-interval curve of the reflective waves is a time-shifted hyperbola in the layered strata. The processing of theoretical model and real data shows that the time-shifted normal moveout and stacking may produce a high-fidelity, high-resolution and accurate stacking image effect. At the same time, the interval velocity derived from the time-shift-corrected spectrum τ0 is more accurate than that derived from the traditional Dix-equation-calculated stacking. This method is not only used for the stacking image of the seismic data in complex area, but also for the flow chart of the high-resolution processing.
-
Key words:
- normal moveout /
- timeinterval curve /
- stack
-
地震反射波的动校正和叠加处理是地震资料数字处理中的关健技术之一.多年来, 在地震资料数字处理中, 一直使用在水平均匀介质假设情况下, 道集上地震反射波时距曲线是以共中心点(common mid point, CMP) 在地面上的投影为原点的双曲线的动校正公式.然而, 对于多数实际中存在的层状介质情况, CMP道集上的反射波时距曲线并不满足共原点双曲线, 因此, 现行的动校正和叠加处理不能取得满意的叠加剖面.
对水平层状介质情况下的反射波时距曲线的表达式, 不少学者曾做过研究, 认为水平层状介质情况下的反射波时距曲线表具有时移双曲线的特征[1, 2].本文通过对前人工作的归纳总结, 将其应用于实际.
1. 时移反射波时距曲线方程
对于水平层状介质情况下的反射波时距曲线, 可用参数方程来描述[3]:
(1) 
(2) 式中: x是炮检距, p=dt/dx是射线参数, Zk是某一层地层的厚度, Vk是某一层地层的速度, N是地层层数.由于pVk < 1, 对(1) 式和(2) 式分别使用二项式展开, 得
(3) 
(4) 式中:
为了求得t作为x的函数, 对(3) 式和(4) 式展成在x=0处的泰勒级数
(5) 式中:
由于t是关于x对称, 所以t是x的偶函数, (5) 式又可进一步表达成
(6a) 或
(6b) 根据Taner等[2]以及Castle[1]的研究结果, (6b) 式中级数展开式的前3项系数是
(7a) 
(7b) 
(7c) 那么, 得到(6) 式级数展开式的前4项的表达式
(8) 应用高斯超几何级数展开, (8) 式可表达成
(9) 令
(10a) 
(10b) 
(10c) 
(10d) 将(10) 式代入(9) 式, 得
(11) (11) 式表明, 水平层状介质情况下, 反射波的时距曲线方程是具有时移量τS的双曲线方程.
2. 时移动校正公式的实现
2.1 时移动校正公式
将(10) 式中τS的表达式代入(11) 式, 整理得
(12) 因为δt=t-t0是CMP道间时差, 所以(11) 式又可表达成
(13) (12) 式和(13) 式即是时移动校正公式.它们与常规动校正公式的区别在于: 动校正的未知量由(t, va) 变成(t, τ0, v).va是叠加速度, v是水平层状介质时距曲线方程中引入的介质速度, 一般来说, v小于va.因此, 在应用时移动校正公式时, 不妨设v等于一小常速度(小于或等于第一层介质速度).
2.2 由静校正实现动校正
根据(13) 式, 可以求得计算地震道的动校正量公式:
(14) 可以看出, (14) 式与t0无直接关系.该方法进行各道的动校正只需要有与炮检距有关的静态时移量、输入介质速度v和叠加前用于CMP资料的聚焦时间τ0.因此, 这种方法不会产生动校正后波形拉伸问题.叠加后地震剖面具有较好的保真度.
2.3 扫描空间的确定
在实施成像分析的过程中, 如果能事先估计出τ0值的范围, 可以较大程度地提高计算效率, 同时又可以节省不必要的资源浪费.比较(13) 式与如下常规的时距曲线方程
(15) 式中: va是叠加速度.
解方程(13) 和方程(15), 得:
(16) 分析(16) 式可知, 当δt的值与τ0和t0的值比较是小数时, 只要能确定处理地震资料所在地区的最大叠加速度值va, 就可确定不同时间所对应的τ0值.
令δt=0, 得
(17) 3. 计算层速度公式
将(12) 式进行级数展开(保留四阶近似), 有
(18) 对比(18) 式与(8) 式, 得
(19) 
(20) (20) 式中的v是第一层介质的速度, 可以看成一常数.那么, (20) 式的差分形式可表示成:
(21) (21) 式即是应用时移动校正公式的成像分析结果计算层速度的公式.
概括起来, 时移动校正和叠加以及层速度计算的实现步骤如下: (1) 输入一个CMP道集; (2) 给出一个初始速度v (一般选浅层最小速度), 用(12) 式对CMP道集中的每一地震道的所有反射时间, 在给定的τ0范围内计算t0值, 形成t0~τ0谱; (3) 对所得到的t0~τ0谱进行分析, 在不同的t0上选取最大能量所对应的τ0值; (4) 将步骤(3) 中的解释结果代入(14) 式, 计算CMP道集中的每一道不同时间段的校正量δt, 然后, 逐段进行校正; (5) 对校正后的地震道叠加; (6) 应用步骤(3) 中的解释结果, 使用(21) 式计算层速度.
4. 计算实例及效果分析
为了验证时移动校正成像方法的有效性, 以下结合理论模型计算结果和实际资料处理结果给予讨论说明.
4.1 层状介质模型
为了验证方法的正确性, 我们设计了一个三层介质模型.第一层为水平反射界面, 双程垂直反射时间为0.6 s, 介质速度为2 000 m/s; 第二层同样是水平反射界面, 双程垂直反射时间为0.9 s, 介质速度为2 500 m/s; 第三层为倾斜反射界面, 倾角为30°, 双程垂直反射时间为1.2 s, 介质速度为3 000 m/s.三层介质模型分析结果如图 1, 从图 1b中可以很清楚地看出时移动校正的成像时间τ0和对应的t0时间.对比图 1c1, 1c2可见: (1) 在常规动校正中, 由于大炮检距记录道的动校存在较严重的拉伸作用, 影响了叠加道的质量; (2) 时移动校正和叠加结果较常规动校正和叠加结果具有较高的保真度.图 2是使用图 1b分析结果计算的层速度结果, 计算结果与给定的模型速度相差较小.
图 1 三层介质模型分析结果a.用射线追踪正演的共同中心点CMP道集记录; b.时移动校正τ0分析谱: b1.CMP记录; b2.τ0分析谱; b3.聚焦能量; c.校正和叠加结果: c1.常规动校正和叠加结果; c2.时移动校正和叠加结果Fig. 1. Analysed result of three＿layer medium model
图 2 层速度计算结果图中实线由时移动校正τ0分析谱, 使用文中(21) 式计算得到, 与实际相差较小; 虚线由常规速度分析, 使用Dix公式计算得到Fig. 2. Caculated interval velocities4.2 实际资料处理及效果分析
图 3a是我国西部某盆地一条经二维精细处理的地震叠加剖面.该区地下受挤压作用成逆推覆地质构造, 造成地下地层产状变化大, 地层速度纵横向变化剧烈, 多处呈速度翻转.勘探目的层较深, 在2.5 s以下.因此, 采用常规的速度分析和动校正叠加方法不能取得满意的结果.图 3b是经时移动校正成像方法得到的地震叠加剖面.与图 3a比较, 时移动校正成像在地震剖面上信噪比高, 所反映的地质构造清楚.
图 3 二维精细(a) 和时移动校正(b) 方法处理的地震叠加剖面由图上可见在CMP190~270的范围内, 3.3 s左右的反射层明显清楚Fig. 3. Processed stack sections by time＿shifted NMO and conventional method5. 结论
时移动校正叠加方法与常规的动校正叠加方法相比具有以下特点: (1) 常规的动校正叠加方法是在假设地下介质为均匀水平界面情况下提出的, 时移动校正叠加方法是在假设地下介质为水平层状地层情况下提出的.因此, 后者较前者更接近实际地层情况. (2) 时移动校正叠加方法对于校正炮检距时差使用静态时移的方法.因此, 它不存在动校正拉伸畸变问题. (3) 实际资料处理表明: 尽管时移动校正方法是在假设地下介质是水平层状地层情况下提出的, 但对于复杂地质构造地区, 它仍然优于常规的动校正叠加方法. (4) 用时移动校正分析谱计算的速度比由叠加速度计算的速度精度要高.
-
图 1 三层介质模型分析结果
a.用射线追踪正演的共同中心点CMP道集记录; b.时移动校正τ0分析谱: b1.CMP记录; b2.τ0分析谱; b3.聚焦能量; c.校正和叠加结果: c1.常规动校正和叠加结果; c2.时移动校正和叠加结果
Fig. 1. Analysed result of three＿layer medium model
图 2 层速度计算结果
图中实线由时移动校正τ0分析谱, 使用文中(21) 式计算得到, 与实际相差较小; 虚线由常规速度分析, 使用Dix公式计算得到
Fig. 2. Caculated interval velocities
-
[1] CastleRJ. A theory of normal moveout[J]. Geophysics, 1994, 5 9 (6): 993~999. [2] Taner M T, Koehler F. Velocity spectra-digital computer derivation and application of velocity functions[J]. Geophysics, 1969, 34: 859~881. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201511009.htm [3] 长春地质学院. 地震勘探[M]. 北京: 地质出版社, 1980. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 3616
- HTML全文浏览量: 544
- PDF下载量: 15
- 被引次数: 0
