Crater Size-Frequency Distribution Measurements and Age Determination of Sinus Iridum
-
摘要: 撞击作用是行星形成和表面重塑的重要地质过程，记录和揭示了行星的演化历史.撞击作用形成的撞击坑可用于研究天体表面地质单元形成的时间.依据内太阳系天体表面的撞击历史，总结了通过对撞击坑的直径和频率分布进行统计，计算天体表面模式年龄的原理和方法.在此基础上，利用美国“月球勘测轨道器(LRO)”广角相机获得的图像，对月球虹湾地区的撞击坑进行了直径-频率分布统计研究，获得其3个主要地质单元的绝对模式年龄分别为3.33 Ga、3.21 Ga和2.60 Ga，有效限定了本区主要地质事件发生的时间.Abstract: Impact cratering is an important process in planet formation and surface modification.It creats impact craters on the surface, which records and reveals the geological history of the planet. It is known that the younger a surface is, the less amount and smaller diameters the craters on that surface are. Therefore, model ages of a surface region of a solid celestial body can be estimated by measuring the crater size-frequency distribution. We summarized the principles and its application, and applied the method to the age determination of Sinus Iridum on the Moon using images obtained by Lunar Reconnaissance Orbiter Wide Angle Camera. Our results show that this region has three main geological units with model ages of 3.33 Ga, 3.21 Ga and 2.60 Ga, respectively.
-
Key words:
- the Moon /
- Sinus Iridum /
- crater size-frequency distribution /
- absolute model age /
- planetary geology /
- geochronology
-
月球是地球的天然卫星，是人类探索太空的前哨站.自1959年开始月球探测至今，人类共进行了100余次月球探测活动.20世纪60~70年代发射的月球探测器有108个，主要集中在美国和前苏联两个超级大国，形成了美苏争霸时期的探月高潮(Harland，2008).在经历了一段平静期后，如今随着美国、欧盟、中国、日本以及印度等国探月计划的提出及实施，月球探测的第二次高潮已经到来.
在月球探测和研究过程中，需要解决的一个基本地质问题是月球地质单元的划分和月表年龄的确定.这对月球地质及演化历史的研究，以及登月着陆点的选取和月球资源的开发等都具有极为重要的意义.
当前国际上对月球表面年龄的研究主要基于以下几种方法：(1)地层叠覆与切割关系研究.通过对不同月球撞击坑溅射物盖层、月海玄武岩单元等的叠覆及切割关系进行研究，获得全月面相对年龄，建立全月球范围内的相对地层序列.但应用该方法确定的地层相对年龄的精度较差，且地层单元的划分也较为粗略(Hiesinger et al., 2000).(2)月球岩石样品的放射性同位素定年.1967—1976年间，美国Apollo计划和苏联Luna计划共从月球上返回样品约382 kg(Harland，2008).通过对这些样品进行放射性同位素定年，可以获得月球表面部分区域的绝对年龄.但是，有精确放射性同位素年龄的月表区域面积很小，仅仅局限于探测器着陆点附近，无法满足对全月地质研究的要求(Stöffler and Ryder, 2001).(3)撞击坑遭受侵蚀状况(crater degradation stages)研究.该方法由Boyce et al.(1974)提出，依据形成时间越早遭受侵蚀程度越高的原理，判断撞击坑分布区地层的相对新老，进而确定大致年龄.但多种内外动力地质过程都可以影响月球撞击坑的改造速率和面貌，不同的地质单元可能不具有可比性，从而降低定年结果的可靠性.事实上，Burgess and Turner(1998)利用40Ar-39Ar法对月球岩石样品进行放射性同位素定年的结果也表明，利用撞击坑侵蚀程度所确定的年龄可能与实际年龄存在较大偏差.(4)撞击坑直径-频率分布定年方法，简称撞击坑统计定年法.该方法是通过对月球表面单位面积上不同直径的撞击坑数量进行统计，并与月球岩石样品的放射性同位素年龄相联系，以确定月球表面绝对模式年龄的方法.本文将重点对此方法进行讨论.
通过对月球表面特定区域撞击坑直径、数量进行测量统计来确定该区域的表面年龄的方法最早由Young于1940年提出(Neukum et al., 2001)；20世纪60年代至今，研究者提出了多种撞击坑直径-频率分布曲线，并进行了一系列修正(Hartmann，1966；Neukum et al., 1972；Neukum et al., 1975a；Neukum and König，1976；Hartmann，1977；Neukum and Ivanov, 1994；Hartmann and Neukum, 2001；Neukum et al., 2001；Hartmann，2005).Neukum et al.(1975b)提出将撞击坑直径-频率测量结果与月球岩石样品的放射性同位素年龄相结合，以获得月球表面绝对模式年龄的方法.Hiesinger et al.(2000)提出利用多光谱图像确定地质单元，以提高撞击坑直径-频率分布定年方法所获取年龄的可靠性，使撞击坑直径-频率分布定年方法获得了进一步完善.
撞击坑直径-频率分布定年方法的基本假设是，撞击坑随机分布且其被破坏的速率远小于撞击坑形成的速率(Hiesinger et al., 2000).因此，月球表面年龄较老的区域由于单位面积上经历的撞击更多，会存在更多的撞击坑，通过研究月球表面撞击坑的直径-频率分布情况，可以得到月球表面不同区域相对年龄的大小.而由于Apollo和Luna号着陆点岩石样品的放射性同位素年龄已经在实验室获得，故建立由撞击坑直径-频率分布关系所获得的该区域相对年龄与样品同位素年龄间的函数关系，即可通过撞击坑直径-频率分布曲线得到月球表面的绝对模式年龄.撞击坑直径-频率分布定年方法也可用于其他行星，如火星、水星、金星等行星表面地质单元绝对模式年龄的测定，但需要考虑这些行星与月球的差异，包括遭受撞击的频率、撞击体的速率分布、行星大气、行星重力场大小以及行星表面物质的物理化学性质等.然后参照月球撞击坑产率函数(Lunar Production Function)推导出其他行星的撞击坑产率函数，进而确定行星表面的绝对模式年龄(Ivanov，2001；Neukum et al., 2001).这是目前行星科学界普遍认同和被广泛应用的行星表面年龄研究方法.
本文将详细阐述利用撞击坑直径-频率分布定年方法确定月球表面年龄的基本原理与方法，进而运用该方法研究月球虹湾地区的绝对模式年龄，并与前人的研究成果进行对比讨论.
1. 撞击坑直径-频率分布定年方法的基本原理
1.1 月球撞击坑产率函数(Lunar Production Function)
利用撞击坑直径-频率分布方法定年，首要问题是建立撞击坑直径与单位面积上该直径撞击坑数量(即撞击坑频率)之间的函数关系.Öpik(1960)利用地基望远镜对月球正面直径大于5~10 km的撞击坑的观测统计表明，撞击坑直径(D)与累积撞击坑频率(Ncum，即单位面积上大于某直径的撞击坑数量)之间的关系近似符合函数Ncum~D-2.Shoemaker(1965)对月球探测器获取的高分辨率图像的研究发现，直径较小的撞击坑，其直径-频率分布曲线的斜率大于直径较大的撞击坑，这一函数关系大致符合Ncum~D-2.9.Neukum et al.(1972)认为Ncum与D之间虽然不是简单的指数关系，但在不同直径范围内的所有撞击坑，其直径-频率关系都近似符合Ncum~D-m这一函数形式.此后，研究者对月球表面更大面积和直径范围内的撞击坑分布情况进行了深入研究(Neukum et al., 1975a, 2001；Neukum and Ivanov, 1994；Ivanov et al., 2002；Hartmann，2005)，提出了目前使用最为广泛的两种分布曲线：Hartmann撞击坑产率函数(简称HPF)和Neukum撞击坑产率函数(简称NPF).
1.1.1 Hartmann撞击坑产率函数
Hartmann(2005)根据撞击坑不同的直径范围，使用一个由三部分组成的分段函数来表示撞击坑直径-频率分布情况.他对直径单元DL＜D＜DR范围内每平方千米的撞击坑数量进行统计，其中DL、DR分别代表单元的左右边界，同时DR又等于下一个相邻单元的左边界.每个标准单元的宽度用以下公式限定：
DR/DL=√2. (1) Hartmann(2005)运用上述方法对月海区域的撞击坑进行统计，并根据统计结果提出月球撞击坑产率函数，该函数反映了年龄约为3.4 Ga的月海表面撞击坑的直径-频率分布情况，其表达式如下：
logNH=−2.616−3.82logDL,0.3km<DL<1.41km.logNH=−2.920−1.80logDL,1.41km<DL<64km.logNH=−2.198−2.20logDL,DL>64km. (2) 式中：NH为对应直径范围内的撞击坑频率.函数中DL的下限为0.3 km，这是因为月海中D＜0.3 km的撞击坑可能已经达到了饱和平衡状态(这是指行星表面某直径范围内的撞击坑密度所达到的一种稳定状态，在此状态下，撞击坑密度足够大，以至于新形成的撞击坑将覆盖较老的撞击坑，使得单位面积内可见的撞击坑数量总体保持不变).此时所获得的年龄不能代表月表的真实年龄(Hartmann，1984；Hartmann and Gaskell, 1997).因此，HPF只能在月球表面尚未达到饱和平衡状态的区域使用.
1.1.2 Neukum撞击坑产率函数
Neukum撞击坑产率函数与HPF不同，其运用一个多项式方程来表示撞击坑直径D与累积撞击坑频率Ncum之间的关系.Neukum and Ivanov(1994)的研究表明，在所有可供进行撞击坑直径-频率分布测量的直径范围内，月球上不同地质单元在不同月球历史时期的撞击坑产率函数曲线的形状是近似相同的，即撞击坑产率函数具有时间独立性.Neukum进而用一条曲线来拟合年龄为1 Ga的月海区域所获得的月球撞击坑直径-频率分布统计数据.该曲线可用如下多项式方程来表示：
logNcum=a0+11∑k=1ak(logD)k, (3) 式中：系数a0与ak的值在表 1中给出.其中a0的数值等于年龄为1 Ga的月海区域单位面积上直径大于1 km的撞击坑数量的对数值，该数值是将撞击坑直径-频率分布统计结果与月球岩石样品的放射性同位素年龄相关联获得(Neukum and Ivanov, 1994；Ivanov，2008).
表 1 Neukum撞击坑产率函数的系数(Neukum et al., 2001)Table Supplementary Table Coefficients in NPF (Neukum et al., 2001)ai 旧数值 新数值 a0 -3.076 8 -3.087 6 a1 -3.626 9 -3.557 528 a2 +0.436 6 +0.781 027 a3 +0.793 5 +1.021 521 a4 +0.086 5 -0.156 012 a5 -0.264 9 -0.444 058 a6 -0.066 4 +0.019 977 a7 +0.037 9 +0.086 850 a8 +0.010 6 -0.005 874 a9 -0.002 2 -0.006 809 a10 -5.181 0-4 +8.251 0-4 a11 +3.971 0-5 +5.541 0-5 Ivanov(2001)、Neukum et al.(2001)对月球东海地区分布的6 700个撞击坑进行了统计，并根据统计结果对NPF曲线进行了重新评估，以使其在较大的撞击坑直径范围内能够更准确的拟合.他们对方程的系数进行了略微修改，修改后的系数和原来的系数都在表 1中列出.
1.1.3 HPF与NPF对比
为了便于对以上两个函数进行对比研究，首先需要引入“相对撞击坑直径-频率分布图”(relative size-frequency distribution plot，即R-plot)来表示以上两个函数.这种表示方法由Arvidson et al.(1979)提出，它可以使原曲线斜率较大的部分变得相对平缓，减小垂向上的长度，而突出曲线中微小的变化，更易于显示出不同曲线间的微小差异.其依据如下公式对撞击坑产率函数进行变换：
R(D)=D3×dNcumdD. (4) 式中：D为撞击坑直径；Ncum为累积撞击坑频率.
利用该公式对HPF和NPF进行处理，并将两曲线投入同一个图中(图 1)，可以发现，在D＜1 km时，两曲线基本重合，在D＞1 km时，HPF曲线逐渐高于NPF曲线，直到D=40 km才再次重合.其中在D=6 km处，两曲线差异最大，HPF数值为NPF的3倍.在40 km≤D≤100 km范围内HPF和NPF较为接近.
图 1 NPF(1)与HPF(2)曲线对比(Ivanov, 2008, 有改动)图中D为撞击坑直径，R为利用公式(4)获得的R(D)值.图中曲线：1.NPF(Neukum et al., 2001)；2.HPF(Hartmann，2005)；3.饱和平衡曲线(Hartmann，1984)Fig. 1. Comparison of NPF(1) and HPF(2)目前，更多的研究者倾向于使用NPF，但究竟哪个函数能更好地反映月表撞击坑的真实分布情况，还有待进一步的研究.尽管如此，在对直径2~40 km范围内的撞击坑分布情况进行研究时应该注意两曲线间差异的存在.
1.2 月球撞击年代曲线
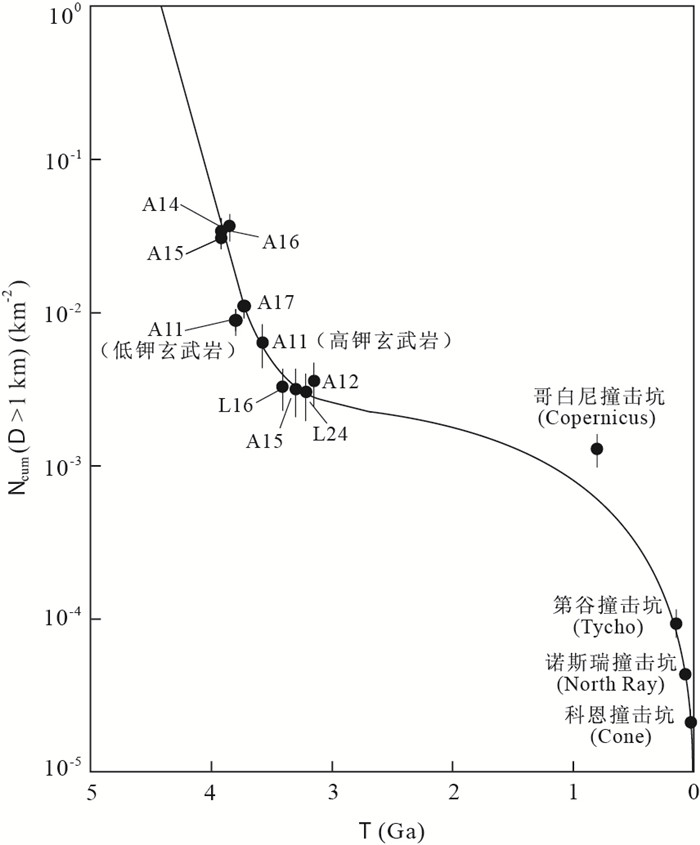
为了利用撞击坑直径-频率分布统计结果获得绝对模式年龄，需要建立累积撞击坑频率与月球表面绝对模式年龄之间的联系.由于Apollo和Luna计划获得了月球部分区域的岩石样品，因此通过对岩石样品进行放射性同位素定年，即可获得这些区域的绝对模式年龄.Neukum et al.(1975a, 2001)、Neukum and Horn(1976)和Neukum and Ivanov(1994)对上述区域的撞击坑直径-频率分布情况进行了统计，并取各区域撞击坑产率曲线上D=1 km所对应的累积撞击坑频率Ncum(D＞1 km).此外，Apollo12、14、16、17等任务获得的岩石样品中，有一部分并非为该区域固有的岩石，而是来自其他大型撞击坑如第谷、哥白尼撞击坑等的溅射物，其放射性同位素年龄多在1 Ga以内，反映了这些大型撞击坑的年龄.因此，Neukum et al.(1975b, 2001)、Neukum and Horn(1976)也在这些大型撞击坑底部进行了撞击坑直径-频率分布情况的统计，按同样的方法获得Ncum(D＞1 km).最后，将各区域Ncum(D＞1 km)与对应岩石样品的放射性同位素年龄进行投图(图 2)，建立月球撞击年代曲线，其表达式如下：
Ncum(D>1km)=5.44×10−14[exp(6.93×t)−1]+8.38×10−4t, (5) 
图 2 月球撞击年代曲线(据Hiesinger et al., 2000, 有简化)图中A代指Apollo，L代指Luna，横坐标T为月球表面绝对模式年龄，纵坐标Ncum(D＞1 km)为单位面积上直径大于1 km的撞击坑总量Fig. 2. Lunar Cratering Chronology Curve其中：t为月球表面相应区域的绝对模式年龄(单位为1 Ga).该曲线是利用撞击坑直径-频率分布定年方法获得月球表面绝对模式年龄的基础.通过该曲线所获得的月表绝对模式年龄的不确定度可由公式(6)确定(Arvidson et al., 1979)：
±σN=log[N(1)±√N(1)A], (6) 式中：N(1)为撞击坑直径-频率分布定年中将Ncum(D＞1 km)代入月球撞击年代曲线所获得的绝对模式年龄.A为进行撞击坑直径-频率分布统计的区域面积.±σN即为所得绝对模式年龄误差的上下限.
2. 虹湾地区地质单元划分及其绝对模式年龄
2.1 虹湾地区地质概况
虹湾位于雨海西北部，中心经纬度为44.10°N、31.50°W(图 3).虹湾东南部与雨海相连，西北部被侏罗山环绕，其直径约236 km，底部总面积约4.5×104 km2，虹湾表面绝大部分区域被玄武岩覆盖.虹湾地区具有众多引人注目的地貌特征，如月溪、熔岩流、皱脊等，有较高的科学研究价值.此外，虹湾底部地形平坦，是登月探测器的理想着陆点之一.
图 3 虹湾的位置及虹湾地区LRO广角相机图像a.虹湾在月球表面的位置，底图为LRO广角相机图像；b.虹湾LRO广角相机图像，图中点线区内为虹湾的范围，白色方框内为二次撞击坑集中分布区Fig. 3. Location of Sinus Iridum and LRO Wide Angle Camera mosaic of Sinus Iridum对虹湾地区年龄的研究始于20世纪60年代，Schaber(1969)利用Lunar Orbiter图像制作了虹湾地区地质图.他通过研究不同区域的反照率和撞击坑密度，并结合地层叠覆关系，将虹湾内的地层按由老到新的顺序分为Im1、Im2和EIm三个主要单元.其中Im1与Im2为晚雨海纪月海玄武岩单元，年龄范围为3.2~3.75 Ga，且Im1比Im2年龄更大，而EIm为爱拉托辛纪月海玄武岩单元，其年龄小于3.2 Ga.但是受到研究方法的限制，Schaber并不能获得各区域的绝对年龄.Boyce and Dial(1975)通过研究撞击坑侵蚀状况获得了虹湾地区的模式年龄，但他们所获得的结果并不精确，只是认为虹湾地区的年龄在3.2~3.5 Ga之间，局部地区可达3.65 Ga.Hiesinger et al.(2000)利用Galileo探测器获取的月球多光谱图像将虹湾地区分为4个区域，并利用Lunar Orbiter高分辨率图像进行撞击坑直径-频率分布测量，获得4个区域的年龄分别为2.96 Ga、3.01 Ga、3.26 Ga和3.39 Ga.本文采用美国2009年发射的探月卫星“月球勘测轨道器(LRO)”广角相机图像，运用撞击坑直径-频率分布定年方法重新研究虹湾地区绝对模式年龄.
2.2 地质单元划分
不同地质单元可能有不同的形成时间，经历了不同的地质事件和演化过程，只有在同一个地质单元内运用撞击坑直径-频率分布定年方法，才能获得较为可靠和有地质意义的年龄.Hiesinger在其一系列论文中提出利用多光谱图像对月海区域进行地质单元划分的方法(Hiesinger et al., 2000, 2003, 2010).该方法选取Clementine多光谱图像415 nm、750 nm和950 nm三个波段进行比值运算，其中415/750比值和750/415比值共同反映月球表面成熟度及Ti含量的变化，而750/950比值则反映Fe的含量，进而根据上述比值合成假彩色图像(Pieters et al., 1994；Li，2011).由于该假彩色图像中不同的颜色反映了不同的成分和反照率，基于同一地质体具有相同的物质组成这一前提，根据图像颜色的变化即可相对准确地划分出不同地质单元.
笔者采用上述方法对Clementine多光谱图像进行处理，获得了虹湾地区假彩色图像(图 4a)，从图中可以明显地划分出颜色不同的3个地质单元(图 4a中黑色实线为地质单元界限)，分别以A、B、C标记，但为了便于讨论，将B单元位于虹湾西南部和东北的两部分分别记为B1和B2.各单元内部由于部分区域存在撞击坑的溅射物盖层而显示出略有不同的颜色，如拉普拉斯A撞击坑(图 4a中以红色箭头标出)周围区域受到其溅射物的覆盖而显示黄绿色.
图 4 虹湾地区地质单元划分与各地质单元定年结果a.虹湾地区地质单元划分与各单元绝对模式年龄.图中黑色虚线内为虹湾范围，黑色实线为各地质单元界限，白色虚线内为进行撞击坑直径-频率分布测量的区域，底图为利用Clementine不同波段比值合成的假彩色图像；b.地质单元A的定年结果；c.地质单元B1的定年结果；d.地质单元B2的定年结果；e.地质单元C的定年结果.图b~e中横坐标为撞击坑直径，纵坐标为累积撞击坑频率Fig. 4. Geologic units in Sinus Iridum and their absolute model ages2.3 虹湾地区绝对模式年龄
本研究利用Neukum et al.(2001)的方法进行撞击坑直径-频率分布测量统计.由于Clementine探测器获得的图像太阳高度角较高，导致能够凸显月面地形的阴影效应在很大程度上被弱化，使较小的撞击坑几乎难以被观测到，且撞击坑的边缘也难以精确划定，不适合进行撞击坑直径-频率分布测量统计.因此，笔者将地质单元边界在分辨率为100 m的LRO广角相机图像上绘出，并在各地质单元内部选取合适的区域(图 4a中白色虚线内)进行撞击坑直径-频率分布测量.
笔者选取的撞击坑直径-频率分布测量范围为0.5~3 km.选择0.5 km作为统计下限是由于LRO广角相机图像的分辨率为100 m，直径过小的撞击坑难以准确确定直径，且很可能是大撞击坑溅射物形成的二次撞击坑；选择3 km作为所统计撞击坑的直径上限是因为虹湾地区面积相对较小，撞击坑总量偏少，将直径过大的撞击坑排除以减小大直径撞击坑对统计结果的误差.
完成撞击坑统计后，将撞击坑按直径分为以下单元：0.5，0.6，0.7，0.8，0.9，1.0，1.1，1.2，1.5，2.0，2.5，然后计算各直径级别上的累积撞击坑频率Ncum，即单位面积上大于该直径的撞击坑总数(表 2)，再将其与对应的直径投图，运用最小二乘法拟合Neukum撞击坑产率曲线，并取拟合后所得曲线上D=1 km处对应的累积撞击坑频率Ncum(D＞1 km).将Ncum(D＞1 km)代入公式(5)，所得t即为研究区域绝对模式年龄(Michael and Neukum, 2010；Huang et al., 2011).
表 2 各区域不同直径单元的累积撞击坑频率Table Supplementary Table Ncum of different diameter units in each area区域 面积(km2) 各直径单元的累积撞击坑频率(km-2) 0.5 km 0.6 km 0.7 km 0.8 km 0.9 km 1.0 km 1.2 km 1.5 km 2.0 km 2.5 km A 4 238.967 2.97e-2 2.17e-2 1.23e-2 8.73e-3 6.84e-3 5.43e-3 3.30e-3 7.08e-4 2.36e-4 0 B1 7 418.919 3.48e-2 1.70e-2 1.05e-2 8.36e-3 5.26e-3 2.97e-3 1.89e-3 6.74e-4 4.04e-4 1.35e-4 B2 3 855.643 3.55e-2 1.89e-2 1.14e-2 8.30e-3 5.19e-3 3.11e-3 1.82e-3 2.59e-4 2.59e-4 0 C 6 288.833 2.56e-2 1.18e-2 8.11e-3 5.41e-3 3.98e-3 3.02e-3 1.59e-3 7.95e-4 3.18e-4 1.59e-4 本研究中，笔者应用craterstats软件(http://hrscview.fu-berlin.de/craterstats.html)，将各区域已按直径分组的累积撞击坑频率数据和区域面积输入该软件，软件可自动拟合撞击坑产率曲线(3)，获得地质单元绝对模式年龄，并依据公式(6)，获得定年误差.
各单元定年结果如图 4a所示，A区域年龄为3.33 Ga，B1和B2区域的年龄皆为3.21 Ga，C区域为2.60 Ga.
3. 讨论
3.1 定年误差的影响因素
在虹湾地区的定年结果中，由月球撞击坑产率函数和月球撞击年代曲线本身的不确定度产生的误差已经由craterstats软件根据公式(6)给出(图 4)，但在对月球表面撞击坑直径、数量统计的过程中，同样存在诸多因素导致误差产生.月球表面的改造过程如熔岩流的覆盖、撞击溅射物的覆盖、新撞击坑的叠覆、月表陡坡的滑坡等都会对撞击坑数量的统计产生影响.二次撞击坑、火山口则会对撞击坑的识别产生干扰.遥感图像本身的质量如分辨率、太阳高度角、拍摄倾角等也会对撞击坑的统计产生较大影响.上述产生误差的因素中，一部分可以较为方便的消除.如可以通过选用分辨率较高、太阳高度角较为合适的LRO或Lunar Orbiter图像进行撞击坑的识别与测量.在此，仅对二次撞击坑、撞击坑叠覆和熔岩流覆盖对定年结果产生的影响进行讨论.
3.1.1 二次撞击坑的影响
二次撞击坑是指散布于原始撞击坑周围一定范围内，由原始撞击产生的溅射物回落到月表形成的撞击坑.较大的撞击会产生数量极多的二次撞击坑，例如Dundas and McEwen(2007)的研究表明，形成第谷撞击坑的撞击事件就产生了超过106个直径大于63 m的二次撞击坑.同时，Xiao and Strom(2012)的研究认为，在利用直径小于1 km的撞击坑进行定年时，可能会在很大程度上受到二次撞击坑的影响，导致定年结果存在较大的不确定性.因此，识别和剔除二次撞击坑就显得至关重要(McEwen and Bierhaus, 2006；Hartmann，2007).
一般而言，具有以下特征的撞击坑通常可以被认为是二次撞击坑(Neukum and König，1976)：首先，沿远离原始撞击坑方向呈链状分布的一系列小撞击坑；其次，椭圆型撞击坑，其长轴方向指向主撞击坑.Nagumo and Nakamura(2001)对二次撞击坑的形状进行了详细研究，他们认为如果椭圆形撞击坑长轴与短轴的比值大于1.2，则可以判定该撞击坑为二次撞击坑.
在虹湾地区，存在几处较为集中的二次撞击坑分布区(图 3b白色方框内)，它们是哥白尼、阿里斯基尔等撞击坑的溅射物盖层(Schaber，1969).为尽可能减小二次撞击坑对统计结果的影响，笔者在确定撞击坑统计区域时尽量避开上述区域.同时，在具体的统计过程中，也识别并剔除了区域内存在的二次撞击坑(表 3).
表 3 各区域二次撞击坑剔除情况Table Supplementary Table Number of eliminated secondary craters in each area区域 撞击坑总数 二次撞击坑数 有效撞击坑数 A 165 39 126 B1 319 61 258 B2 173 36 137 C 192 28 164 3.1.2 撞击坑的叠覆
月表在漫长的演化历史中，早期形成的撞击坑可能会被后来的撞击坑覆盖.除此之外，小的撞击事件以及撞击坑的溅射物也会使已形成的撞击坑遭到破坏，而直径较小的撞击坑最容易受到此类过程的影响.Moore、Gault等通过对月面撞击坑的统计以及实验室模拟证明, 月球表面的撞击坑数量最终会趋近于一个平衡状态，该状态下撞击坑遭到破坏而消失的速率等于新撞击坑产生的速率(Neukum et al., 1975a)，而Hartmann(1984)的研究则表明在饱和平衡状态下撞击坑的直径-频率分布情况大致服从如下函数：
logNHC=−1.83logDkm−1.33, (7) 式中：NHC为饱和平衡区域的撞击坑频率；Dkm为撞击坑直径.
在虹湾地区定年过程中，笔者将Hartmann饱和平衡函数导入craterstats软件，生成平衡曲线，并在图 4b~4e中显示，上述各图中饱和平衡曲线均在所投各点的上方，说明研究区域在不同直径范围内均未达到饱和平衡状态，符合撞击坑直径-频率定年方法的适用要求，其结果具有可靠性.
3.1.3 熔岩流覆盖
月球在其形成之初，经历了多期较为强烈的火山活动，它们直到30亿年前才逐步减弱(Hiesinger et al., 2000).火山活动形成的熔岩流会覆盖月球表面的部分区域，对这些区域撞击坑的数量产生重大的影响(Neukum and Horn, 1976；Neukum et al., 2010).
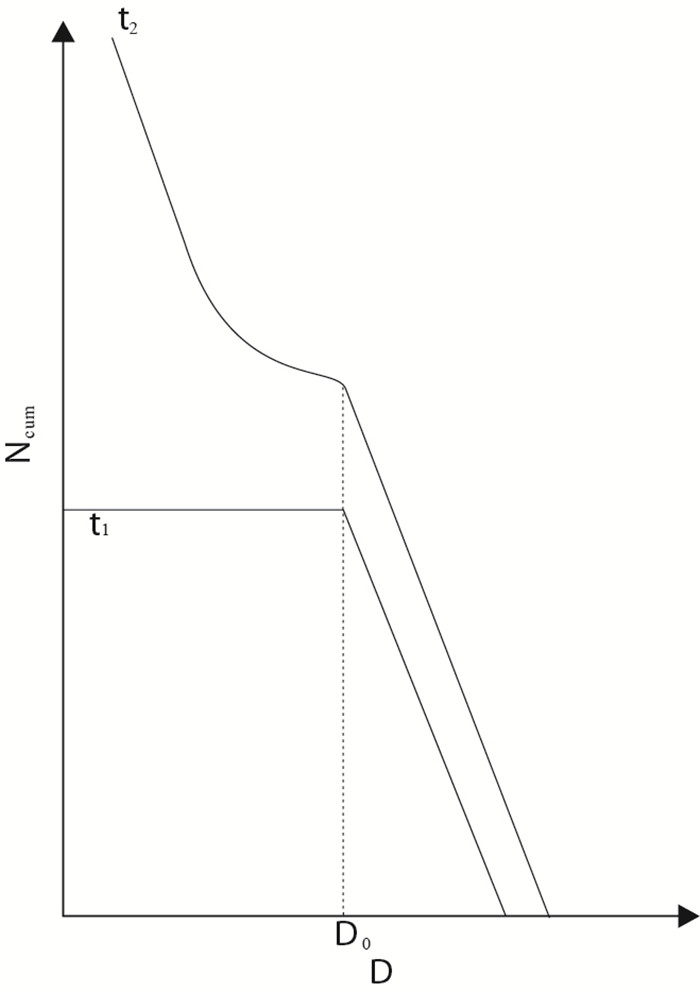
熔岩流覆盖对撞击坑数量的影响主要与熔岩流的厚度及撞击坑的规模有关.一定厚度的熔岩流会导致小于某一规模的撞击坑被覆盖，而大于这一规模的撞击坑则会保存下来(Hiesinger et al., 2002；Platz et al., 2010).假设在t0时刻一块新鲜(即不存在撞击坑)的月表区域开始遭受撞击，若不考虑其他的干扰因素，如撞击坑叠覆和其他破坏撞击坑的过程，那么在任何时刻该区域上撞击坑的直径-频率分布情况都将符合撞击坑产率函数曲线.接下来，如果在t1时刻该表面经历了熔岩流的覆盖过程，小于直径D0的撞击坑完全被覆盖，那么撞击坑直径-频率分布曲线则会相应发生改变.此时，在D≤D0的范围内，撞击坑累积频率为常数，即分布曲线变为水平.这一过程之后，撞击坑会在原有的基础上继续积累，到t2时刻，该区域存在的撞击坑既有t1时刻未被覆盖的撞击坑，也有t1~t2时刻之间新积累的撞击坑.那么，t2时刻的撞击坑直径-频率分布曲线在D＞D0的范围内会基本和t1时刻的曲线平行，且在t1时刻的曲线上方；在D=D0处，曲线会突然趋向于水平，因为t1时刻熔岩流的覆盖导致当时直径小于D0的撞击坑全部缺失，因而此处的撞击坑累积频率保持恒定；在D＜D0时，曲线的斜率会逐步变大直至恢复到与所在直径范围内标准撞击坑产率曲线的斜率相同(图 5).因此，经历了一次熔岩流覆盖过程的区域，其撞击坑直径-频率分布曲线会明显的分为两段，各自与一条独立的等时线吻合，故在该区域会获得两个不同的绝对模式年龄.其中较老的年龄为该区域的形成年龄，而较新的年龄近似等于t1到t2所经历的时间.事实上，较新的年龄会略大于t1到t2实际间隔的时间，因为累积撞击坑频率会受到t0-t1时段积累的而未被熔岩流覆盖的撞击坑数量的影响.
表 4 虹湾地区地质年龄(所属地层)对比(单位：Ga)Table Supplementary Table Comparison of ages and stratigraphy for Sinus Iridum in billion years地质单元 年龄(本文) 所属地层 Hiesinger(2000) Schaber(1969) A 3.33 Im1 3.26 Im1/Im2 B 3.21 Im2 3.01/3.39 Im1/Im2 C 2.60 EIm 2.96 EIm Hiesinger(2000)的研究结果据 Hiesinger et al.(2000) ；Schaber(1969)的研究结果据Schaber(1969).
图 5 熔岩流覆盖对撞击坑直径-频率分布曲线的影响(据Neukum et al., 1976, 有改动)图中横坐标为撞击坑直径，纵坐标为累积撞击坑频率.t1表示t1时刻撞击坑直径-频率分布曲线；t2指t2时刻撞击坑直径-频率分布曲线；D0为t1时刻熔岩流所覆盖的撞击坑的直径上限Fig. 5. Effects of lava flow on crater size-frequency distribution curve在虹湾地区各地质单元的定年曲线中并未明显显示出熔岩流覆盖的特征，这可能是因为熔岩流对直径较小的撞击坑具有较大影响，而本文所统计的撞击坑的直径下限为0.5 km，该统计范围内的撞击坑受熔岩流覆盖的影响较小，定年结果依然具有较高的可靠性.
3.2 定年结果比较
本研究获得的虹湾地区各地质单元的绝对模式年龄，按照美国地质调查局的月球地层划分方案(Schaber，1969)，A区域属Im1，B区域为Im2，而C区域为EIm，这和美国地质调查局出版的月球地质图集中该区域存在的地层单元基本一致，但在区域的划分上存在差别.与Hiesinger et al.(2000)的结果对比，Hiesinger同样将虹湾地区划分为4个区域，且4个区域的分布范围与本研究中所划分区域的范围大致相同，但各单元间的地质界限并不精细.此外，Hiesinger认为B1、B2并非同一地质单元，且B2单元的时代较B1单元更老，而单元A的年龄则介于B1与B2之间.这一方面是由于Hiesinger所利用的Galileo多光谱图像的空间分辨率为2 km，远小于Clementine探测器图像250m的空间分辨率.Hiesinger采用409 nm、562 nm、756 nm三个波段进行波段运算，计算结果与本研究采用的Clementine多光谱图像415 nm、750 nm和950 nm波段进行运算所得的结果也有所不同.另一方面，Hiesinger进行撞击坑直径-频率分布测量的下限为0.8 km，且撞击坑统计区域面积较小，故所统计的有效撞击坑数相对较少，精度较低.在本文的定年结果中，B1、B2区域皆为3.21 Ga，这很好地验证了所划分地质单元的准确性.
4. 结论
撞击坑直径-频率分布定年方法是确定月球表面绝对模式年龄较为精确、完善的方法.二次撞击坑、熔岩流覆盖、撞击坑叠覆等因素会对定年结果产生影响，需要在定年过程中结合实际情况进行处理.
本文利用撞击坑直径-频率分布定年方法重新研究了虹湾地区的绝对模式年龄，通过对定年结果的分析，可以得出以下结论：地层Im1在虹湾地区分布最广，年龄最老，为3.33 Ga，属晚雨海纪；地层Im2分布在虹湾西南部和东北部，年龄为3.21 Ga，为晚雨海纪；地层EIm分布在虹湾西南部与雨海相接处，年龄为2.60 Ga，属爱拉托辛纪.
致谢: 本文利用的美国LRO数据来自http://pds.jpl.nasa.gov，平面制图利用了JMARS for Earth's Moon (http://jmars.asu.edu)，数据处理利用了Craterstats(http://hrscview.fu-berlin.de/craterstats.html)，数据处理过程得到了中国地质大学(武汉)行星科学研究所何琦老师和肖智勇博士的帮助，在此谨表谢意.此外，感谢两名匿名评审专家对本文提出的建设性修改意见. -
图 1 NPF(1)与HPF(2)曲线对比(Ivanov, 2008, 有改动)
图中D为撞击坑直径，R为利用公式(4)获得的R(D)值.图中曲线：1.NPF(Neukum et al., 2001)；2.HPF(Hartmann，2005)；3.饱和平衡曲线(Hartmann，1984)
Fig. 1. Comparison of NPF(1) and HPF(2)
图 2 月球撞击年代曲线(据Hiesinger et al., 2000, 有简化)
图中A代指Apollo，L代指Luna，横坐标T为月球表面绝对模式年龄，纵坐标Ncum(D＞1 km)为单位面积上直径大于1 km的撞击坑总量
Fig. 2. Lunar Cratering Chronology Curve
图 3 虹湾的位置及虹湾地区LRO广角相机图像
a.虹湾在月球表面的位置，底图为LRO广角相机图像；b.虹湾LRO广角相机图像，图中点线区内为虹湾的范围，白色方框内为二次撞击坑集中分布区
Fig. 3. Location of Sinus Iridum and LRO Wide Angle Camera mosaic of Sinus Iridum
图 4 虹湾地区地质单元划分与各地质单元定年结果
a.虹湾地区地质单元划分与各单元绝对模式年龄.图中黑色虚线内为虹湾范围，黑色实线为各地质单元界限，白色虚线内为进行撞击坑直径-频率分布测量的区域，底图为利用Clementine不同波段比值合成的假彩色图像；b.地质单元A的定年结果；c.地质单元B1的定年结果；d.地质单元B2的定年结果；e.地质单元C的定年结果.图b~e中横坐标为撞击坑直径，纵坐标为累积撞击坑频率
Fig. 4. Geologic units in Sinus Iridum and their absolute model ages
图 5 熔岩流覆盖对撞击坑直径-频率分布曲线的影响(据Neukum et al., 1976, 有改动)
图中横坐标为撞击坑直径，纵坐标为累积撞击坑频率.t1表示t1时刻撞击坑直径-频率分布曲线；t2指t2时刻撞击坑直径-频率分布曲线；D0为t1时刻熔岩流所覆盖的撞击坑的直径上限
Fig. 5. Effects of lava flow on crater size-frequency distribution curve
表 1 Neukum撞击坑产率函数的系数(Neukum et al., 2001)
Table 1. Coefficients in NPF (Neukum et al., 2001)
ai 旧数值 新数值 a0 -3.076 8 -3.087 6 a1 -3.626 9 -3.557 528 a2 +0.436 6 +0.781 027 a3 +0.793 5 +1.021 521 a4 +0.086 5 -0.156 012 a5 -0.264 9 -0.444 058 a6 -0.066 4 +0.019 977 a7 +0.037 9 +0.086 850 a8 +0.010 6 -0.005 874 a9 -0.002 2 -0.006 809 a10 -5.181 0-4 +8.251 0-4 a11 +3.971 0-5 +5.541 0-5 
下载: 导出CSV
表 2 各区域不同直径单元的累积撞击坑频率
Table 2. Ncum of different diameter units in each area
区域 面积(km2) 各直径单元的累积撞击坑频率(km-2) 0.5 km 0.6 km 0.7 km 0.8 km 0.9 km 1.0 km 1.2 km 1.5 km 2.0 km 2.5 km A 4 238.967 2.97e-2 2.17e-2 1.23e-2 8.73e-3 6.84e-3 5.43e-3 3.30e-3 7.08e-4 2.36e-4 0 B1 7 418.919 3.48e-2 1.70e-2 1.05e-2 8.36e-3 5.26e-3 2.97e-3 1.89e-3 6.74e-4 4.04e-4 1.35e-4 B2 3 855.643 3.55e-2 1.89e-2 1.14e-2 8.30e-3 5.19e-3 3.11e-3 1.82e-3 2.59e-4 2.59e-4 0 C 6 288.833 2.56e-2 1.18e-2 8.11e-3 5.41e-3 3.98e-3 3.02e-3 1.59e-3 7.95e-4 3.18e-4 1.59e-4
下载: 导出CSV
表 3 各区域二次撞击坑剔除情况
Table 3. Number of eliminated secondary craters in each area
区域 撞击坑总数 二次撞击坑数 有效撞击坑数 A 165 39 126 B1 319 61 258 B2 173 36 137 C 192 28 164
下载: 导出CSV
表 4 虹湾地区地质年龄(所属地层)对比(单位：Ga)
Table 4. Comparison of ages and stratigraphy for Sinus Iridum in billion years
地质单元 年龄(本文) 所属地层 Hiesinger(2000) Schaber(1969) A 3.33 Im1 3.26 Im1/Im2 B 3.21 Im2 3.01/3.39 Im1/Im2 C 2.60 EIm 2.96 EIm Hiesinger(2000)的研究结果据 Hiesinger et al.(2000) ；Schaber(1969)的研究结果据Schaber(1969).
下载: 导出CSV
-
Arvidson, R., Boyce, J., Chapman, C., et al., 1979. Standard Techniques for Presentation and Analysis of Crater Size-Frequency Data. Icarus, 37: 467-474. doi: 10.1016/0019-1035(79)90009-5 Boyce, J.M., Dial, A.L., 1975. Relative Ages of Flow Units in Mare Imbrium and Sinus Iridum. In: Merrill, R.B., ed., Proceedings of the Sixth Lunar Conference. Pergamon Press, New York, 2585-2595. Boyce, J.M., Dial, A.L., Soderblom, L.A., 1974. Ages of the Lunar Nearside Light Plains and Maria. In: Gose, W.A., ed., Proceedings of the Fifth Lunar Conference. Pergamon Press, New York, 11-23. Burgess, R., Turner, G., 1998. Laser Argon-40-Argon-39 Age Determinations of Luna 24 Mare Basalts. Meteoritics & Planetary Science, 33(4): 921-935. doi: 10.1111/j.1945-5100.1998.tb01697.x Dundas, C.M., McEwen, A.S., 2007. Rays and Secondary Craters of Tycho. Icarus, 186: 31-40. doi: 10.1016/j.icarus.2006.08.011 Harland, D.M., 2008. Exploring the Moon: The Apollo Expiditions. Springer, Berlin, 363-371. doi: 10.1007/978-0-387-74641-8 Hartmann, W.K., 1966. Early Lunar Cratering. Icarus, 5: 406-418. doi: 10.1016/0019-1035(66)90054-6 Hartmann, W.K., 1977. Relative Crater Production Rates on Planets. Icarus, 31: 260-276. doi: 10.1016/0019-1035(77)90037-9 Hartmann, W.K., 1984. Does Crater 'Saturation Equilibrium' Occur in the Solar System? Icarus, 60: 56-74. doi: 10.1016/0019-1035(84)90138-6 Hartmann, W.K., 2005. Martian Cratering 8: Isochron Refinement and the Chronology of Mars. Icarus, 174: 294-320. doi: 10.1016/j.icarus.2004.11.023 Hartmann, W.K., 2007. Martian Cratering 9: Toward Resolution of the Controversy about Small Craters. Icarus, 189: 274-278. doi: 10.1016/j.icarus.2007.02.011 Hartmann, W.K., Gaskell, R.W., 1997. Planetary Cratering 2: Studies of Saturation Equilibrium. Meteoritics & Planetary Science, 32: 109-121. doi: 10.1111/j.1945-5100.1997.tb01246.x Hartmann, W.K., Neukum, G., 2001. Cratering Chronology and the Evolution of Mars. Space Science Reviews, 96(1-4): 165-194. doi: 10.1023/A:1011945222010 Hiesinger, H., Head III, J.W., Wolf, U., et al., 2002. Lunar Mare Basalt Flow Units: Thicknesses Determined from Crater Size-Frequency Distributions. Geophysical Research Letters, 29(8): 89-81 - 89-84. doi: 10.1029/2002GL014847 Hiesinger, H., Head III, J.W., Wolf, U., et al., 2003. Ages and Stratigraphy of Mare Basalts in Oceanus Procellarum, Mare Nubium, Mare Cognitum, and Mare Insularum. Journal of Geophysical Research, 108(E7): 5065-5091. doi: 10.1029/2002JE001985 Hiesinger, H., Head III, J.W., Wolf, U., et al., 2010. Ages and Stratigraphy of Lunar Mare Basalts in Mare Frigoris and Other Nearside Maria Based on Crater Size-Frequency Distribution Measurements. Journal of Geophysical Research, 115(E3): E03003. doi: 10.1029/2009JE003380 Hiesinger, H., Jaumann, R., Neukum, G., et al., 2000. Ages of Mare Basalts on the Lunar Nearside. Journal of Geophysical Research, 105(E12): 29239-29275. doi: 10.1029/2000JE001244 Huang, J., Xiao, L., He, X.X., et al., 2011. Geological Characteristics and Model Ages of Marius Hills on the Moon. Journal of Earth Science, 22(5): 601-609. doi: 10.1007/s12583-011-0211-8 Ivanov, B.A., 2001. Mars/Moon Cratering Rate Ratio Estimates. Space Science Reviews, 96(1-4): 87-104. doi: 10.1023/A:1011941121102 Ivanov, B.A., 2008. Size-Frequency Distribution of Asteroids and Impact Craters: Estimates of Impact Rate. In: Adushkin, V.V., Nemchinov, I.V., eds., Catastrophic Events Caused Cosmic Objects. Springer Netherlands, Berlin, 91-116. doi: 10.1007/978-1-4020-6452-4_2 Ivanov, B.A., Neukum, G., Bottke, W., et al., 2002. The Comparison of Size-Frequency Distributions of Impact Craters and Asteroids and the Planetary Cratering Rate. In: Bottke, W.F., ed., Asteroids III. University of Arizona Press, Tucson, 89-101. Li, L., 2011. Quantifying TiO2 Abundance of Lunar Soils: Partial Least Squares and Stepwise Multiple Regression Analysis for Determining Causal Effect. Journal of Earth Science, 22(5): 549-565. doi: 10.1007/s12583-011-0206-5 McEwen, A.S., Bierhaus, E.B., 2006. The Importance of Secondary Cratering to Age Constraints on Planetary Surfaces. Annual Review of Earth and Planetary Sciences, 34: 535-567. doi: 10.1146/annurev.earth.34.031405.125018 Michael, G.G., Neukum, G., 2010. Planetary Surface Dating from Crater Size-Frequency Distribution Measurements: Partial Resurfacing Events and Statistical Age Uncertainty. Earth and Planetary Science Letters, 294: 223-229. doi: 10.1016/j.epsl.2009.12.041 Nagumo, K., Nakamura, A.M., 2001. Reconsideration of Crater Size-Frequency Distribution on the Moon: Effect of Projectile Population and Secondary Craters. Advances in Space Research, 28: 1181-1186. doi: 10.1016/S0273-1177(01)00488-4 Neukum, G., Basilevsky, A.T., Kneissl, T., et al., 2010. The Geologic Evolution of Mars: Episodicity of Resurfacing Events and Ages from Cratering Analysis of Image Data and Correlation with Radiometric Ages of Martian Meteorites. Earth and Planetary Science Letters, 294: 204-222. doi: 10.1016/j.epsl.2009.09.006 Neukum, G., Ivanov, B.A., Hartmann, W.K., 2001. Cratering Records in the Inner Solar System in Relation to the Lunar Reference System. Space Science Reviews, 96(1-4): 55-86. doi: 10.1023/A:1011989004263 Neukum, G., Ivanov, B.A., 1994. Crater Size Distributions and Impact Probabilities on Earth from Lunar, Terrestrial-Planet, and Asteroid Cratering Data. In: Gehrels, T., Matthews, M.S., Schumann, A., eds., Hazards due to Comets and Asteroids. The University of Arizona Press, Tucson, 359. Neukum, G., Horn, P., 1976. Effects of Lava Flows on Lunar Crater Populations. Earth, Moon, and Planets, 15(3-4): 205-222. doi: 10.1007/BF00562238 Neukum, G., König, B., 1976. Dating of Individual Lunar Craters. In: Merrill, R.B., ed., Proceedings of the Seventh Lunar Conference. Pergamon Press, New York, 2867-2881. Neukum, G., König, B., Arkani-Hamed, J., 1975a. A Study of Lunar Impact Crater Size-Distributions. Earth, Moon, and Planets, 12(2): 201-229. doi: 10.1007/BF00577878 Neukum, G., König, B., Fechtig, H., et al., 1975b. Cratering in the Earth-Moon System: Consequences for Age Determination by Crater Counting. In: Merrill, R.B., ed., Proceedings of the Sixth Lunar Conference, New York, 2597-2620. Neukum, G., Schneider, E., Mehl, A., et al., 1972. Lunar Craters and Exposure Ages Derived from Crater Statistics and Solar Flare Tracks. In: King, E.A., Heymann, D., Criswell, D.R., eds., Proceedings of the Third Lunar Science Conference. The MIT Press, Cambridge, MA, 2793-2810. Öpik, E.J., 1960. The Frequency of Crater Diameters in Mare Imbrium. Astronomical Journal, 65: 55. Pieters, C.M., Staid, M.I., Fischer, E.M., et al., 1994. A Sharper View of Impact Craters from Clementine Data. Science, 266(5192): 1844-1848. doi: 10.1126/science.266.5192.1844 Platz, T., Michael, G.G., Neukum, G., 2010. Confident Thickness Estimates for Planetary Surface Deposits from Concealed Crater Populations. Earth and Planetary Science Letters, 293: 388-395. doi: 10.1016/j.epsl.2010.03.012 Schaber, G.G., 1969. Geologic Map of the Sinus Iridum Quadrangle of the Moon. In: U.S. Geological Survey, ed., Geologic Atlas of the Moon. U.S. Geological Survey, Washington, D.C., I-602. Shoemaker, E.M., 1965. Preliminary Analysis of the Fine Structure of the Lunar Surface in Mare Cognitum. In: Hess, W.N., Menz, D.H., O'Keefe, J.A., eds., The Nature of the Lunar Surface: Proceedings of the 1965 IAU-NASA Symposium. The Johns Hopkins Press, Baltimore, MD, 23. Stöffler, D., Ryder, G., 2001. Stratigraphy and Isotope Ages of Lunar Geologic Units: Chronological Standard for the Inner Solar System. Space Science Reviews, 96(1-4): 9-54. doi: 10.1023/A:1011937020193 Xiao, Z.Y., Strom, R.G., 2012. Problems Determining Relative and Absolute Ages Using the Small Crater Population. Icarus, 220: 254-267. doi: 10.1016/j.icarus.2012.05.012 -
下载:
点击查看大图
计量
- 文章访问数: 4458
- HTML全文浏览量: 758
- PDF下载量: 356
- 被引次数: 0
