Reliability Analysis of Stability of Fill Slope
-
摘要: 为了系统地建立填土边坡稳定性的可靠度分析方法, 首先, 在可靠度分析原理的基础上, 对填土边坡的不确定性进行了讨论; 然后, 建立了多变量影响下填土边坡可靠度分析的基本流程; 最后, 以广西平乐县二塘锰矿区典型填土边坡为例, 基于GeoStudio软件, 应用所提出的分析流程对典型填土边坡的可靠度指标进行了计算, 通过"安全概率"对边坡的安全性进行了评价.研究结果表明: (1)填土边坡的不确定性包括内部结构和环境因素两方面, 前者不确定因素来自于填土土体不确定性和边坡的几何特征不确定性, 后者不确定性因素来自于降雨、地震和人工加载等; (2)可靠度分析的基本流程为填土边坡系统不确定性分析、建立可靠度极限状态方程、求解可靠度指标和边坡安全性评价; (3)广西平乐二塘锰矿填土边坡敏感性因素排序为: 内摩擦角Φ＞黏聚力C＞车辆荷载F; (4)考虑50年一遇极值降雨过程, 稳定性系数在降雨12 h达到最小, 其可靠度指标(β)为8.79, 破坏概率为0.根据《滑坡防治工程设计与施工技术规范》所规定的安全系数, 填土边坡的安全概率为69.84%.Abstract: In order to analyze reliability of the stability of fill slopes, first, uncertain factors of stability of slope are discussed on the basis of the reliability theory. Then, the basic process of reliability analysis of fill slope is established, considering multi-variables. Finally, we apply the proposed method to analyze typical fill slope in manganese mine located at Ertang village, Pingle county, Guangxi. Results show that the fill slope uncertainties include two aspects, namely, internal structure and environmental factors. The former is due to the uncertainty of soil and slope geometric characteristics, and the latter is due to the rainfall, earthquakes, artificial load and so on. The reliability analysis contains three steps including analyzing uncertainty of fill slope, establishing the equation of reliability analysis, calculating reliability index and evaluating slope safety. The sensitivity factors for analyzing slope stability is internal friction angle Φ > cohesion C > vehicle load F. When Considering the maximum rainfall of 50 years return period, the stability is lowest at 12 h in one rain course. Its reliability index (β) is 8.79 and the failure probability is 0. According to the safety factor of criterion, the safe probability of the fill slope is 69.84%.
-
Key words:
- slope stability /
- reliability analysis /
- system uncertainty /
- safety probability /
- engineering geology
-
0. 引言
我国人均土地面积少的现实和政府对建设用地指标严格控制的政策，使得相当多的城市与工业区建设向坡荒地和矿山废弃地发展，由此常常要以大规模的填方工程来平整场地，并随之形成大量的填土边坡.显然，这些填土边坡属于永久性边坡，其稳定性对后期工程建设至关重要.
利用填方工程形成的建设场地，其土体强度与稳定性取决于填土的物理力学性质和当地自然因素的影响程度，当然也与填土高度和施工技术条件有关.提供填土的取土场往往就近选定，或直接利用所整平建设场地的挖方区土源，其填土质量既无法得到保证，又因为人工挖掘、搬运、填筑、压实等环节的影响，使填土边坡土体性质更是复杂，其边坡稳定性较之一般天然边坡也更具有不确定性.
由于边坡工程的一系列设计基本参数具有不确定性，人们已经充分认识到了边坡系统具有非确定性或随机性(姚耀武和陈东伟, 1994; Chowdhury and Xu, 1995)，为此，可靠性分析方法成为评价边坡系统不确定性因素的有效手段.岩土工程可靠性研究已经得到了学者们的高度重视，土木工程可靠度设计也进入了实质性应用阶段，并先后制订了铁路、公路、港工、水利等工程可靠度设计统一标准，对岩土工程可靠性设计提出了新要求.在边坡稳定可靠度研究方面，人们对其基本原理和分析方法已经有了一些探索，但对于具有显著非均质性的填土及不确定性的填土边坡的可靠度分析研究较少.因此，针对目前大量出现的建设场地填土边坡，开展其稳定可靠度研究就显得十分必要.
1. 可靠度分析原理
可靠性理论于20世纪70年代逐渐开始在边坡工程领域获得应用.尤其是近20年来, 国内外许多学者对边坡系统的相关性以及不确定性的认识不断深入(罗文强等, 2002), 可靠性理论在边坡可靠性评价和风险分析方面的应用取得重大的进展.
边坡的可靠度通常通过稳定性概率(ps)、破坏概率(pf)或可靠指标(β)3个参数来表示，他们之间具有如下的关系：
ps+pf=1,pf=Φ(−β). (1) 考虑边坡稳定性受多种因素(状态变量) 的控制，用状态变量来构造斜坡稳定性的状态函数：
Z=g(X1,X2,⋯,Xn), (2) 函数g(X)反映边坡的稳定状态，与状态变量X有关，X为斜坡系统的主要结构和环境要素.由于一些状态变量具有随机性和不确定性，使得状态Z表现出不确定性.
状态函数(2)用极限方程Z=0进行描述时，公式(3)构成n维空间的极限状态曲面，可将空间划分为稳定(Z＞0)、破坏(Z＜0)两个区域.
Z=g(X)=g(X1,X2,⋯,Xn)=0. (3) 可靠指标β是边坡状态函数的平均值与标准差的商，或是在n维状态空间中，坐标原点到n维极限状态面的最短距离.求解可靠指标常用方法有Monte Carlo模拟法、可靠指标法(中心点法，JC法等)、统计矩近似法、随机有限元法等.本文采用GeoStudio软件中的Monte Carlo法计算可靠度指标.
2. 填土边坡的不确定性
填土边坡的不确定性包括内部结构和环境因素两方面的不确定性，其中，结构不确定因素来自于边坡的填土土体不确定性和边坡的几何特征不确定性两个方面，环境因素的不确定性来自于降雨、地震和人工加载等因素的不确定性.
2.1 填土边坡的土体不确定性
填土边坡的土体不确定性，主要是因为填土性质的不确定性和填筑施工的不确定性.
2.1.1 土性的不确定性
土性的不确定性的主要表现在土的固有变异性和试验参数不确定性方面.
(1) 土的固有变异性.填土经历了漫长的地质时期，如果将土体看作一个系统，其性质取决于土的组成与结构，并受到环境条件的影响.在土的形成过程中不断地受到自然条件以及人类活动的影响，致使土体在组成与结构上呈现出各向异性与非均质性等特点，即土体性质存在不确定性.由于土的分类存在一定的差异性，即使是均匀的同类土层，在其长期的形成过程中，由于土层深度、应力历史、矿物成分、含水量和结构等因素的变化，各点(处)土的性质也可能存在较大差别，而这是土体本身所固有的差异，即土的固有变异性，反映的是土体性质的空间差异性和不确定性.
在一定的时空条件下，土的物质组成与结构是相对稳定的，其性质是可确定，即可以用确定的数值对其物理力学性质进行描述.但是，随着土体组成与结构的自身演化，或者环境条件的改变，其性质也处于不断变化之中.因而从时间尺度上而言，土体性质具有不确定性.
(2) 土性试验参数的不确定性.尽管上面已经述及对于具体的时空条件，可以用确定的数值描述土体性质.但是，由于人们认识的局限性和获取描述土性参数的试验手段的有效性不足，使得土体性质参数的“真”值往往是未知或难知的，它的大小只能通过有限的室内或现场试验的量测或观察去了解，其测值是变化的，具有时间和空间尺度效应，而且离散性很大，具有很强的不确定性.
从已有的研究成果看，在自然地质成因条件下，土体强度参数多服从正态分布和对数正态分布(李远耀等, 2008).
2.1.2 填土边坡施工引起土体结构的不确定性
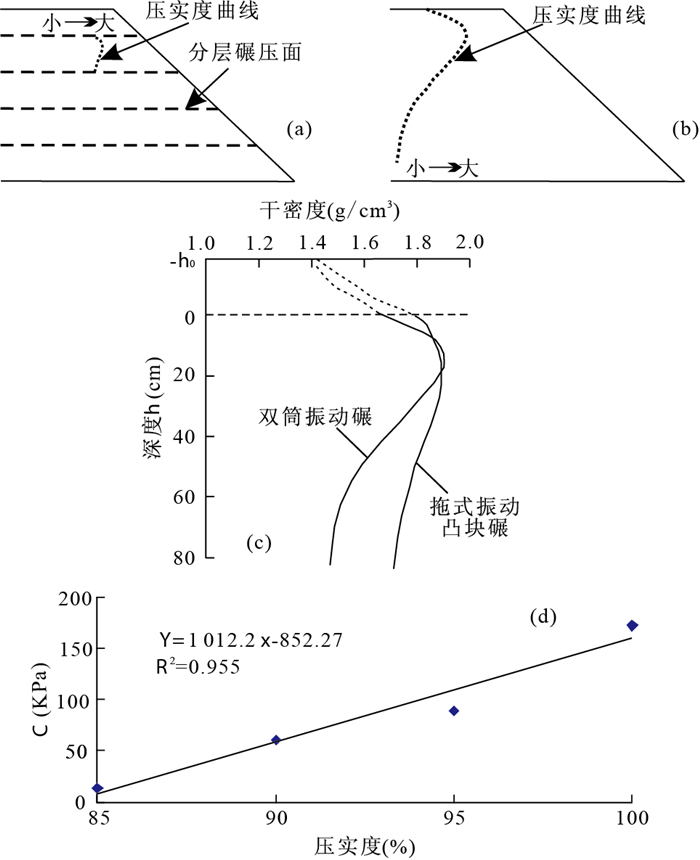
填土边坡施工技术、时间和施工质量的控制表现出明显的不确定性.填土施工中，可采用分层压实和强夯等施工技术，使填土达到设计压实度.由于施工技术的不同，填筑后的土坡表现出明显不同的压密组合结构，前者形成类似多层结构的土坡，后者为两层结构土坡.根据不同路碾对压实层厚度影响的检测结果，双筒振动碾和拖式振动凸块碾在表层以下15~25 cm处压实度最大，表层和深部压实度减小(陈团结和贾润萍, 2002)，填土压实度(λ)随深度(h)在空间上的分布可以看作对数正态分布的一部分(图 1)，通过公式(4)的计算模型进行描述.根据压实度和填土强度C、φ值的关系，两者之间呈正相关性(图 1).
λ(h)=1(h+h0)σ√2πe−(lnh+h0−μ)2/2σ2, (4) 
图 1 不同施工技术填土结构特征(据陈团结和贾润萍, 2002)a.分层压实填土结构；b.强夯法填土结构；c.不同压实技术填土压实度分布情况；d.平乐二塘锰矿填土压实度和黏聚力关系Fig. 1. Fill soil structure of different compaction methods式中：λ(h)为深度h处填土压实度；μ为对数分布压实度均值；σ为压实度方差；h0为地表压实度截距深度(图 1).
施工持续时间(施工速度)及施工后固结时间，使填土表现为回弹变形或固结变形两种不确定的性质.对施工质量的控制也是填土结构不确定性的主要影响因素，即便是加密现场检测的密度和频率也很难覆盖整个填土边坡，为此填土边坡施工引起土体结构的不确定性应在可靠度分析中予以考虑.
在建立边坡稳定性计算模型时，重点考虑边坡施工后的填土组合结构和随时间的变化过程，继而建立其强度参数的时空分布模型.
2.2 填土边坡几何特征不确定性
填土边坡是由原始地形和填土后斜坡组成的几何边界，填土后的坡面有明确的坡率设计要求，属于相对确定性几何边界，而原始地形在边坡不同部位形态有所差异.这就使得填土边坡破坏面的几何形态表现出不确定性，存在几种常见的形式：(1)当原始地形为陡坡，填土厚度不大的情况下，破坏面几何形态受控于原始地面，常沿填土和原斜坡面破坏；(2)当填土厚度大时，破坏面位于填土内部，几何形态与剪应力增量集中区的形状近乎一致.按照已有的土坡稳定性分析理论，当填土均匀时，破坏面的形态为圆弧状，但实际的填土边坡观测结果表明，在填土不完全均匀的情况下，存在上陡、下缓的抛物线型滑面.
为探讨上陡、下缓型滑面边坡的稳定性，将破坏面近似看作抛物线形，设滑动面的方程为：
y=px2 (5) 滑面的倾角，可表示为：tanα=y'=2px，有：
sinα=tanα√1+tan2α=2px√1+(2px)2cosα=1√1+tan2α=1√1+(2px)2}. (6) 把公式(5)与公式(6)用于瑞典条分法(ordinary)可得到公式(7)所示的稳定性计算：
FS=γtanφ{∫a0[y1(x)−y(x)]1√1+(2px)2dx+∫ba[y2(x)−y(x)]1√1+(2px)2dx}+c∫b0√1+(2px)2dxγ∫a0[y1(x)−y(x)]2px√1+(2px)2dx+γ∫ba[y2(x)−y(x)]2px√1+(2px)2dx. (7) 由公式(7)可知，稳定系数FS是参数p(滑弧形状参数)的函数，通过MATLAB搜索典型填土边坡(均匀填土)最危险滑动面，该填土边坡的最小稳定性系数为1.15，对应的p值为0.04.即，滑动面方程为：y=0.04x2，该稳定性系数小于圆弧法所计算的稳定性(图 2).
在可靠度分析时，应在在填土结构、力学参数分析的基础上，考虑填土边坡破坏面的几何特征，按照最先达到临界状态的几何边界作为可靠度分析的模型边界.
2.3 填土边坡外部环境的不确定性
2.3.1 降雨
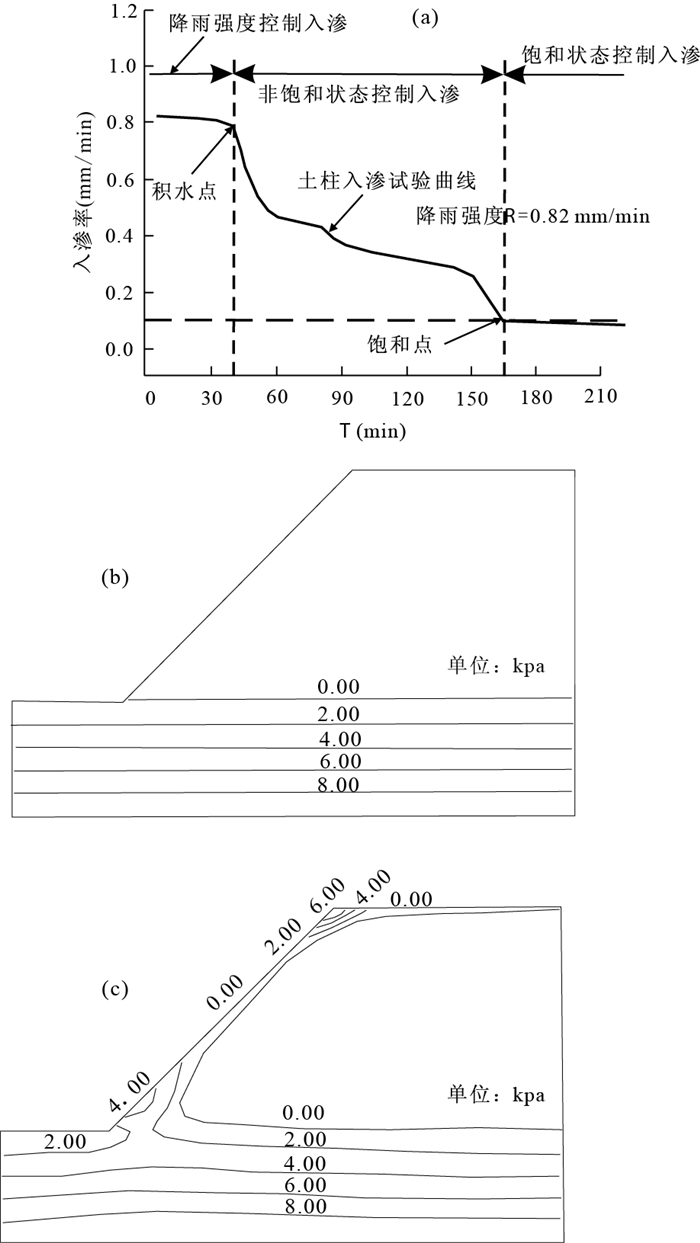
降雨是一个不确定性事件，常用重现期和极值来描述降雨的不确定性，边坡失稳常与降雨的各种极值具有密切联系.目前，边坡稳定性可靠度分析多注重对降雨概率的描述，用极值降雨量来分析边坡的可靠度，但常常忽略不同类型降雨入渗量的差异性，也即降雨环境对边坡系统的真实输入和响应过程，从图 3a中可知在恒定降雨条件下边坡入渗过程可分为3个阶段，初期入渗率受降雨强度控制，降雨几乎全部入渗，随着降雨的持续坡面出现积水点，受非饱状态土的控制，入渗率下降，当达到饱和点时降雨入渗稳定，为饱和渗透系数(朱伟等, 2006).
从填土边坡的实际情况看，大部分边坡无稳定渗流场(图 3b)，仅在降雨期间形成非饱和带或短时的饱和带(图 3c).边坡稳定性对降雨的响应表现为强度参数下降和饱和带水力消散引起的渗透作用两方面(孙冬梅等，2007).
降雨及入渗过程造成边坡的非饱和渗流，可通过数值模拟的方法实现，在得到边坡土体的孔隙水压力后，应用非饱和土强度理论分析降雨作用下边坡的稳定性变化.
2.3.2 地震
在区域地壳不稳定地区，地震对填土边坡施加动荷载，是促使边坡失稳的重要外因.为了简化计算，常将地震荷载看成与动峰值加速度ae有关的固定荷载，荷载大小为F=aeM，M为边坡失稳部分的质量.根据已有研究，地震时地面水平峰值加速度多服从极大值分布，在边坡可靠度分析时，边坡系统所受地震荷载值也服从极大值分布.
2.3.3 人工加载
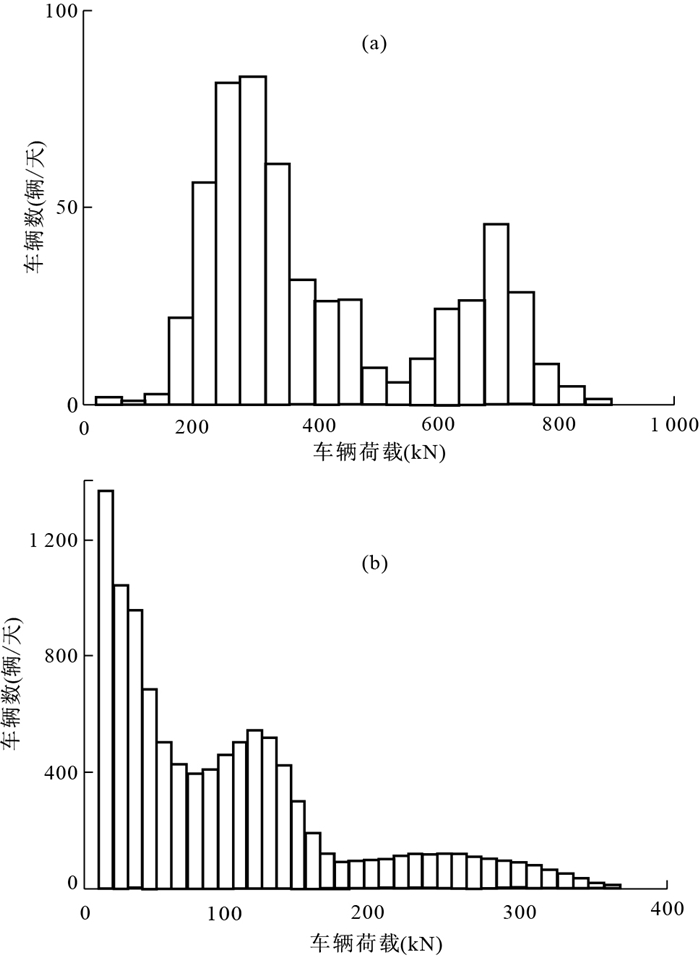
人工加载主要来自于边坡上的永久建筑物和车辆荷载，其中，建筑物和设计活荷载是人为赋予边坡的固定荷载，可以看成一个确定性问题.但诸多填土边坡在实际运营过程中，常遇到车辆动荷载问题，车辆荷载服从双峰值或多峰值分布模型(梅刚等，2003；郭彤等，2008)，图 4a中为110国道可测车辆荷载的分布直方图，2个峰值分别对应于普通货车和满载煤的重型货车，图 4b中为京沪高速公路(江苏段)行车道和超车道车辆荷载直方图，表现为三峰值的特征，分别代表轻型车辆、普通车辆和重型货车的荷载.各峰值可通过最小二乘法或极大似然估计法进行拟合，拟合值服从正态分布或对数正态分布.
对于填土边坡造成边坡失稳事件主要来源于重型货车或超限超载车辆，为此，在失稳可靠度分析时主要针对重型货车，也即是双峰或多峰分布图中相对较大的荷载峰值.
3. 填土边坡稳定性的可靠度分析流程
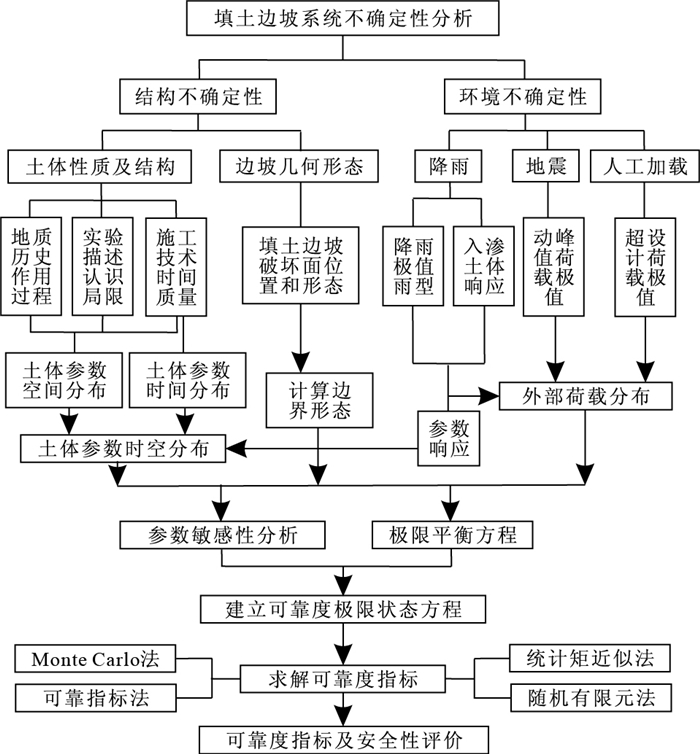
填土边坡稳定性可靠度分析的基本流程包括4部分：填土边坡系统不确定性分析、建立可靠度极限状态方程、求解可靠度指标和边坡安全性评价(图 5).
(1) 填土边坡系统不确定性分析：前述填土边坡不确定性中已经详细分析，需建立系统主要组成结构和外部环境的不确定性集合.从系统稳定性评价的计算模型看，该不确定性结合是由时空分布参数、计算边界条件和外部荷载分布组成.
(2) 建立可靠度极限状态方程：建立边坡稳定性计算的极限平衡方程时，应以边界形态和假定的破坏模式为基础，选择传统的刚体极限平衡方程作为计算模型.为了简化可靠度指标求解的过程，尽量少考虑参数的不确定性，在建立可靠度极限状态方程前，还需要通过参数敏感性分析对不确定性参数进行筛选.
(3) 求解可靠度指标：利用已有的可靠度求解模型进行计算，这部份在可靠度分析原理中已经述及.
(4) 边坡安全性评价：得到可靠度指标后，可求解边坡破坏概率或稳定性概率，再根据有关规范对边坡等级和安全系数之间的关系，分析边坡安全等级所对应的安全概率.
4. 广西平乐二塘锰矿区填土边坡稳定性的可靠度分析
矿区位于广西桂林市东南部的平乐县二塘镇.由于露天开采锰矿，地貌已全部遭到破坏，矿坑、矿槽和土堆相间分布，地面高差可达20~30 m.目前，锰矿资源开采殆尽，为缓和平乐县招商引资与城市用地紧张的困境，计划将闭坑的平乐二塘锰矿区改造成建设用地，把全县工业集中从城区转移至此.对二塘锰矿区场地整平工程，在场区周边形成了大面积的填土边坡(图 6)，对填土边坡的可靠度分析可指导边坡的施工设计.
4.1 边坡不确定性因素分析
(1) 边坡填土组成物质和结构：填土来自于采矿遗留的渣土，原岩为残坡积含碎石、锰质结核的粉质粘土，由于人工挖采后成为松散的渣土，混杂有灰岩、页岩块石，因此，组成物质的天然结构和强度参数具有不确定性.设计采用重力强夯对填土进行结构夯实，填土结构压实度服从强夯施工工艺的分布模型.利用室内土工试验分析填土在设计压实度情况下的物理力学参数见表 1.
表 1 平乐二塘锰矿区典型填土边坡可靠度分析参数Table Supplementary Table Typical fill slope reliability analysis parameters in Ertang Manganese Mine, Pingle统计特征 填土物理参数 降雨量 车辆加载kN 粘聚力C(KPa) 重度γ(kN/m3) Φ(°) 次降雨量重现期(mm) 降雨强度(mm/h) 均值 23 17.4 19.5 20 a/250 20 a/15 250.7 50 a/300 50 a/20 方差 1.80 1.50 1.50 51.3 概率模型 正态分布 正态分布 正态分布 极值分布 极值分布 正态分布 (2) 边坡几何形态：按照前面的分析，几何形态存在圆弧、抛物线的形态，其中针对二塘锰矿区分析结果见表 2，以抛物线形态参数p为0.04时稳定性系数最低.
表 2 填土边坡不同滑面最小稳定性系数结果比较Table Supplementary Table Minimum stability coefficient of fill slope with different slip surface项目名称 本文(抛物线)法 圆弧法 ordinary Bishop 最小稳定性系数 1.15 1.39 1.50 滑动面形状 抛物线形 圆弧形 (3) 降雨影响参数：矿区属亚热带季风气候区，全年降雨量平均值为1 807.6，其中3~8月汛期降雨量平均值分别为130.7 mm、116.7 mm、184.1 mm、355.6 mm、334.2 mm和343.1 mm.利用赵华荣等(2011)对桂林50年丰水期降雨量的分析曲线，可得到丰水期年季变化趋势和丰水期降雨量的重现期.根据王金叶等(2012)对漓江上游森林群落降雨量的研究，桂林地区在丰水期以暴雨为主，降雨强度和降雨量之间具有较好的相关性，在2011年丰水期，最大降雨16 h达319.8 mm，降雨强度达20.0 mm/h.次降雨强度大于50 mm，平均降雨强度为9.87 mm/h.矿区不同重现期次降雨量和降雨强度的经验参数见表 1.
(4) 地震：区内地震烈度为Ⅵ度，在边坡设计和可靠度分析时，不需要考虑地震作用.
(5) 人工加载参数：根据工业场区的规划，填土边坡为工业区边界，以车辆荷载为主.根据规划车辆多为工业区运送原材料和商品的货车，按照重型货车的荷载分布参数，具体见表 1.
4.2 极限平衡方程和敏感性分析
在对填土边坡破坏模式的分析时，将破坏滑动面近似为圆弧形或抛物线型.考虑到大部分规范中规定滑面为圆弧形，推荐计算方法为瑞典条分法(ordinary)和Bishop法，本文应用利用GeoStudio软件的Slope/W模块自带的计算方法，分别采用瑞典条分法(ordinary)、Bishop、Janbu和Morgenstern-Price(M-P) 法进行计算，除Janbu法按照力平衡计算稳定性和可靠度，其他方法选取力矩平衡.
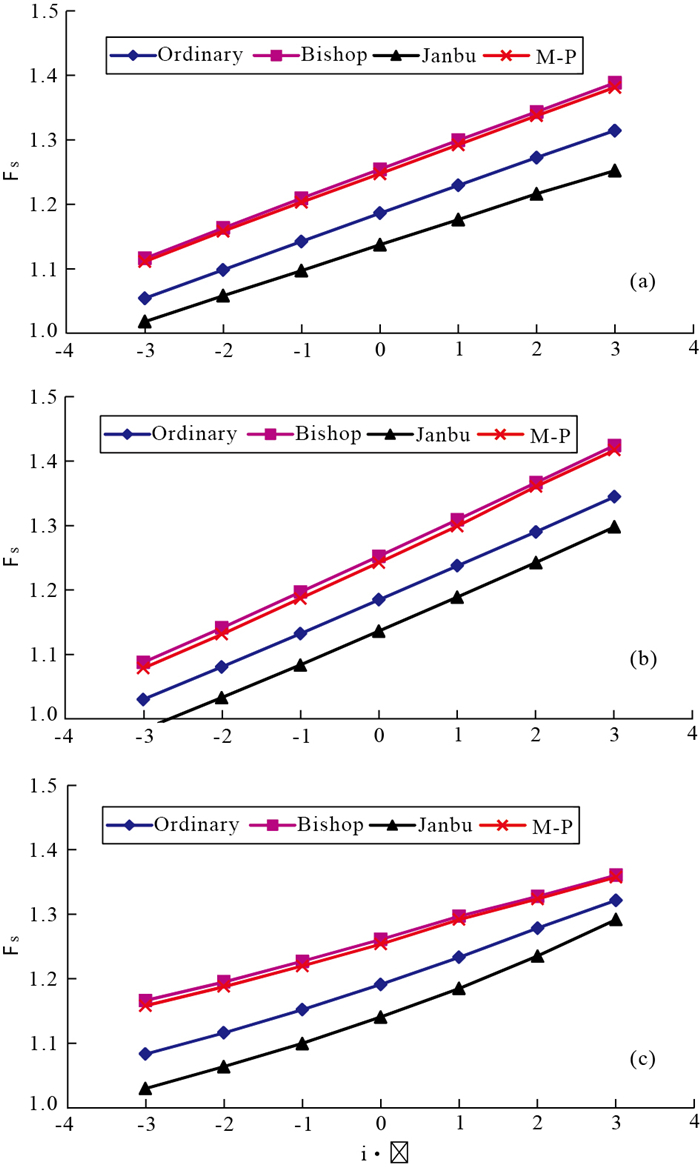
在敏感性分析时，选择平乐二塘锰矿区一个典型填土边坡进行参数敏感性分析，填土边坡高11.5 m，坡度45°，不考虑孔隙水压力影响.大量研究成果显示，敏感参数为岩土的强度参数、外部荷载和降雨，为此，该边坡选择黏聚力C、内摩擦角Φ和车辆荷载F进行敏感性分析，考虑填土随深度压实度变化造成的重度变化(图 7)，3个敏感性分析参数变化值分布在±3σ内(柴波等，2007).单参数敏感性分析中不变参数见表 1中的均值.
敏感性分析结果见图 8，计算结果显示，Janbu法计算稳定性系数最低、Bishop法计算稳定性系数最大，在变化6倍方差的情况下，3个参数稳定性变化的平均值分别为：0.259、0.328和0.218，敏感性排序为：内摩擦角Φ＞黏聚力C＞车辆荷载F，为此，可靠度分析时，车辆荷载可采用固定值.
图 8 单参数敏感性分析解结果a.C值敏感性图；b.Φ值敏感性图；c.F值敏感性图Fig. 8. Single parameter sensitivity analysis4.3 求解可靠度指标
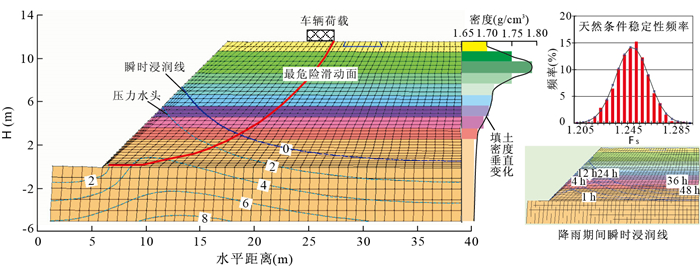
可靠度分析将岩土强度参数作为随机分布函数，考虑其空间变异性，雨量选择极值分布的20年和50年重现期暴雨.由于篇幅原因，只介绍50年重现期极值暴雨条件下填土边坡的可靠度.首先，建立暴雨情况下，填土边坡渗流分析模型，根据填土颗粒分析结果和饱和含水率，利用经验参数建立非饱和土的土水特征曲线和渗透系数函数.利用Seep/W模拟降雨期间(1 d)和降雨后1 d的孔隙水压力分布(图 7)，将模拟结果代入Slope/W中分析边坡的破坏概率和可靠度，稳定性平均值的计算结果如表 3和图 9，表中显示，即便是一次降雨过程，其稳定性系数随时间发生变化，在可靠度分析时，选择最小稳定性系数的时刻进行可靠度分析，即降雨12 h时.
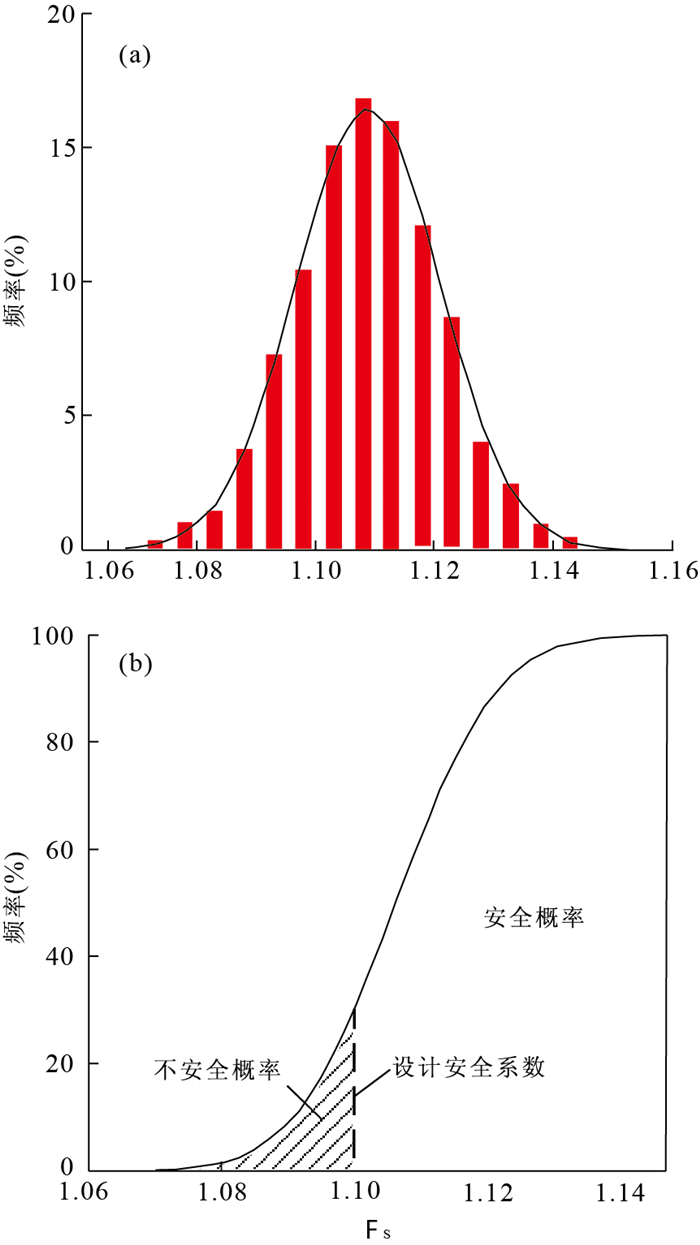
表 3 50年重现期极值雨量边坡稳定性均值Table Supplementary Table Mean stability coefficient of fill slope with rainfall of 50-year return period时间(h) 计算方法 ordinary Bishop Janbu M-P 0 1.189 1.251 1.152 1.245 1 1.161 1.221 1.128 1.215 4 1.143 1.200 1.112 1.195 12 1.059 1.106 1.036 1.102 24 1.076 1.137 1.048 1.132 36 1.093 1.176 1.057 1.169 48 1.100 1.183 1.063 1.176 
图 9 50年重现期极值雨量边坡稳定性均值变化曲线Fig. 9. Mean curve of slope stability with maximum rainfall of 50-year return period利用Slope/W中边坡破坏概率和可靠度分析功能，计算50年重现期极值雨量12 h的稳定性系数概率分布函数和累计分布函数曲线见图 10，图中为Bishop法计算结果，稳定性系数均值为1.106 3，破坏概率(pf)为0，可靠指标(β)为8.79.
图 10 50年重现期极值雨量边坡稳定性概率a.稳定性分布概率；b.稳定性累计概率Fig. 10. Slope stability probability with maximum rainfall of 50-year return period4.4 边坡安全性评价
根据可靠度指标的定义，填土边坡的稳定性系数均大于1，破坏概率为0.评价边坡是否需要治理或安全的依据是安全系数，为此，将安全系数引入可靠度分析，提出安全概率或不安全概率的概念，前者为大于安全系数的概率，后者为小于安全系数的概率.
在不同的技术规范中，对于边坡安全系数的定义不尽相同，其中《建筑边坡工程技术规范》中边坡安全系数是根据边坡安全等级和计算方法确定的，圆弧滑动法中二级边坡的安全系数为1.25，此时，该边坡的不安全概率为100%.《滑坡防治工程设计与施工技术规范》中规定了滑坡荷载、计算方法和防治工程设计安全系数，Ⅱ级滑坡设计时选择20年重现期降雨量，用瑞典条分法进行稳定性计算，校核时采用50年重现期雨量，用Bishop方法进行校核，设计安全系数为1.02~1.15，本文选择1.10所对应的概率作为不安全概率，其值为30.16%，相应的安全概率为69.84%.
5. 结论
(1) 填土边坡的不确定性包括内部结构和环境因素两方面，前者不确定因素来自于填土土体不确定性和边坡的几何特征不确定性，后者不确定性因素来自于降雨、地震和人工加载等.
(2) 填土边坡稳定性可靠度分析的基本流程包括4部分：填土边坡系统不确定性分析、建立可靠度极限状态方程、求解可靠度指标和边坡安全性评价.
(3) 广西平乐二塘锰矿填土边坡敏感性因素排序为：内摩擦角Φ＞黏聚力C＞车辆荷载F.
(4) 考虑50年一遇极值降雨过程，稳定性系数在降雨12 h达到最小，其可靠度指标(β)为8.79，破坏概率为0.《滑坡防治工程设计与施工技术规范》所规定的安全系数，填土边坡的安全概率为69.84%.
-
图 1 不同施工技术填土结构特征(据陈团结和贾润萍, 2002)
a.分层压实填土结构；b.强夯法填土结构；c.不同压实技术填土压实度分布情况；d.平乐二塘锰矿填土压实度和黏聚力关系
Fig. 1. Fill soil structure of different compaction methods
图 8 单参数敏感性分析解结果
a.C值敏感性图；b.Φ值敏感性图；c.F值敏感性图
Fig. 8. Single parameter sensitivity analysis
图 9 50年重现期极值雨量边坡稳定性均值变化曲线
Fig. 9. Mean curve of slope stability with maximum rainfall of 50-year return period
图 10 50年重现期极值雨量边坡稳定性概率
a.稳定性分布概率；b.稳定性累计概率
Fig. 10. Slope stability probability with maximum rainfall of 50-year return period
表 1 平乐二塘锰矿区典型填土边坡可靠度分析参数
Table 1. Typical fill slope reliability analysis parameters in Ertang Manganese Mine, Pingle
统计特征 填土物理参数 降雨量 车辆加载kN 粘聚力C(KPa) 重度γ(kN/m3) Φ(°) 次降雨量重现期(mm) 降雨强度(mm/h) 均值 23 17.4 19.5 20 a/250 20 a/15 250.7 50 a/300 50 a/20 方差 1.80 1.50 1.50 51.3 概率模型 正态分布 正态分布 正态分布 极值分布 极值分布 正态分布 
下载: 导出CSV
表 2 填土边坡不同滑面最小稳定性系数结果比较
Table 2. Minimum stability coefficient of fill slope with different slip surface
项目名称 本文(抛物线)法 圆弧法 ordinary Bishop 最小稳定性系数 1.15 1.39 1.50 滑动面形状 抛物线形 圆弧形
下载: 导出CSV
表 3 50年重现期极值雨量边坡稳定性均值
Table 3. Mean stability coefficient of fill slope with rainfall of 50-year return period
时间(h) 计算方法 ordinary Bishop Janbu M-P 0 1.189 1.251 1.152 1.245 1 1.161 1.221 1.128 1.215 4 1.143 1.200 1.112 1.195 12 1.059 1.106 1.036 1.102 24 1.076 1.137 1.048 1.132 36 1.093 1.176 1.057 1.169 48 1.100 1.183 1.063 1.176
下载: 导出CSV
-
Chai, B., Yin, K.L., Wang, Y., et al., 2007. Sensitivity Analysis of Landslide Stability Based on Distribution Models of Influencing Factors. Rock and Soil Mechanics, 28(12): 2624-2628 (in Chinese with English abstract). Chen, T.J., Jia, R.P., 2002. Correct Application of Subgrade Compaction Method and Reasonable Cutting Ring Sampling Depth. Journal of Highway and Transportation Research and Development, 19(6): 45-47, 51 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GLJK200206012.htm Chowdhury, R.N., Xu, D.W., 1995. Geotechnical System Reliability of Slopes. Reliability Engineering and System Safety, 47(3): 141-151. doi: 10.1016/0951-8320(94)00063-T Guo, T., Li, A.Q., Zhao, D.L., 2008. Multiple-Peaked Probabilistic Vehicle Load Model for Highway Bridge Reliability Assessment. Journal of Southeast University (Natural Science Edition), 38(5): 763-766 (in Chinese with English abstract). http://d.wanfangdata.com.cn/Periodical/dndxxb200805005 Li, Y.Y., Yin, K.L., Chai, B., et al., 2008. Study on Statistical Rule of Shear Strength Parameters of Soil in Landslide Zone in Three Gorges Reservoir Area. Rock and Soil Mechanics, 29(5): 1419-1425 (in Chinese with English abstract). http://d.wanfangdata.com.cn/Periodical/ytlx200805053 Luo, W.Q., Zhang, Z.Y., Huang, R.Q., et al., 2002. Advances in the Research on Reliability on Slope System. Earth Science Frontiers, 7(S2): 105-111 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DXQY2000S2016.htm Mei, G., Qin, Q., Lin, D.J., 2003. Bi-Modal Probabilistic Model of Highway and Bridge Vehicle Loads. Journal of Tsinghua University (Sci. & Tech. ), 43(10): 1394-1396, 1404 (in Chinese with English abstract). http://d.wanfangdata.com.cn/periodical/qhdxxb200310026 Sun, D.M., Zhu, Y.M., Zhang, M.J., 2007. Water-Air Two-Phase Flow Model for Numerical Analysis of Rainfall Infiltration. Shuili Xuebao, 38(2): 150-156 (in Chinese with English abstract). http://www.cqvip.com/QK/90347X/200702/23952013.html Wang, J.Y., Li, H.F., Duan, W.J., et al., 2012. Research on Rainfall Characteristics through Typical Forest Community. Research of Soil and Water Conservation, 19(1): 56-59 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-STBY201201013.htm Yao, Y.W., Chen, D.W., 1994. Analysis of Reliability Index in Slope Stability. Chinese Journal of Geotechnical Engineering, 16(2): 80-87 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-CQJT2007S1019.htm Zhao, H.R., Xia, B.C., Jiang, X.D., 2011. Characteristics of Precipitation Change in Guilin Last 50 Years. Journal of Guilin University of Technology, 31(2): 202-206 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GLGX201102008.htm Zhu, W., Chen, X.D., Zhong, X.C., 2006. Observation and Analysis of Rainfall Infiltration. Rock and Soil Mechanics, 27(11): 1873-1879 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-YTLX200611002.htm 柴波, 殷坤龙, 汪洋, 等, 2007. 基于影响因素分布模型的滑坡稳定性敏感分析. 岩土力学, 28(12): 2624-2628. doi: 10.3969/j.issn.1000-7598.2007.12.027 陈团结, 贾润萍, 2002. 填土路基压实方法与环刀法取样深度中的误区. 公路交通科技, 19(6): 45-47, 51. doi: 10.3969/j.issn.1002-0268.2002.06.013 郭彤, 李爱群, 赵大亮, 2008. 用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型. 东南大学学报(自然科学版), 38(5): 763-766. doi: 10.3321/j.issn:1001-0505.2008.05.005 李远耀, 殷坤龙, 柴波, 等, 2008. 三峡库区滑带土抗剪强度参数的统计规律研究. 岩土力学: 29(5): 1419-1425. doi: 10.3969/j.issn.1000-7598.2008.05.053 罗文强, 张倬元, 黄润秋, 等, 2002. 斜坡系统可靠性分析研究. 地学前缘, 7(S2): 105-111. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY2000S2016.htm 梅刚, 秦权, 林道锦, 2003. 公路桥梁车辆荷载的双峰分布概率模型. 清华大学学报(自然科学版), 43(10): 1394-1396, 1404. doi: 10.3321/j.issn:1000-0054.2003.10.026 孙冬梅, 朱岳明, 张明进, 2007. 降雨入渗过程的水-气二相流模型研究. 水利学报, 38(2): 150-156. doi: 10.3321/j.issn:0559-9350.2007.02.004 王金叶, 李海防, 段文军, 等, 2012. 漓江上游典型森林群落内外降雨特征研究. 水土保持研究, 19(1): 56-59. https://www.cnki.com.cn/Article/CJFDTOTAL-STBY201201013.htm 姚耀武, 陈东伟, 1994. 土坡稳定可靠度分析. 岩土工程学报, 16(2): 80-87. doi: 10.3321/j.issn:1000-4548.1994.02.010 赵华荣, 夏北成, 江学顶, 2011. 桂林市近50年降雨变化特征分析. 桂林理工大学学报, 31(2): 202-206. doi: 10.3969/j.issn.1674-9057.2011.02.006 朱伟, 陈学东, 钟小春, 2006. 降雨入渗规律的实测与分析. 岩土力学, 27(11): 1873-1879. doi: 10.3969/j.issn.1000-7598.2006.11.003 -
下载:
点击查看大图
计量
- 文章访问数: 3645
- HTML全文浏览量: 767
- PDF下载量: 739
- 被引次数: 0
