0.   引言

20世纪50年代，Jacob(1950)推导了海岸线垂直下切条件下一维承压含水层地下水潮汐效应的解析解.此后，许多学者进一步研究获得了一些更为复杂条件下地下水潮汐效应的解析解(李国敏和陈崇希，1991；Jiao and Tang，1999；Li and Jiao，2001，2002；杨颖等，2008；夏玉强和李海龙，2009；Guo et al.，2010；Dong et al.，2012；王礼恒等，2012；宋超等，2013；Asadi-Aghbolaghi et al.，2014；Wang et al.，2014；Huang et al.，2015；陈斌等，2016)，但是他们多数是对承压含水层地下水潮汐效应和水文地质参数开展研究，而对潜水含水层地下水潮汐效应和水文地质参数求解方法的研究相对较少(Li et al.，2002，2006; Chang et al.，2010；Yeh et al.，2010)，且这些研究往往将水文地质模型和潮汐水位波动概化得比较简单，主要是因为潜水含水层地下水的潮汐效应远不如承压含水层那么敏感，潜水含水层受潮汐效应影响并没有引起人们的高度重视.笔者的野外观测和研究表明：虽然潮汐对潜水含水层地下水水位变幅以及影响范围较小，但滨岸带潜水含水层地下水水位的小幅往复涨落会对地下水中溶质的迁移产生显著影响，因而开展潜水含水层地下水潮汐效应及其水文地质参数确定方法的研究对于进一步探讨潜水含水层中地下水溶质迁移规律是十分必要的.

1.   区域水文地质特征

1.1   地下水潮汐动态特征

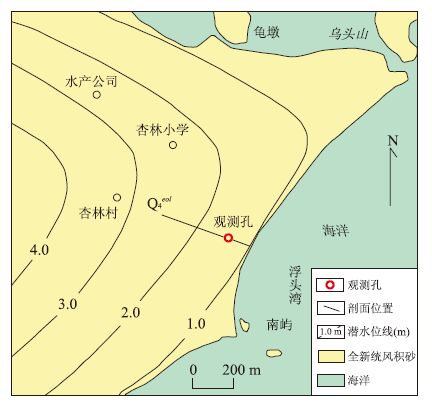
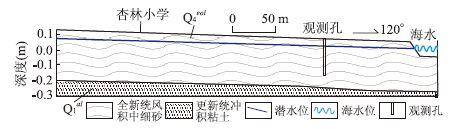
研究区位于福建省漳州市漳浦县古雷半岛东侧浮头湾海滨，本区表层为第四系全新统风积中细砂孔隙潜水含水层(Q₄^eol)，厚度约为35 m，其下由更新统冲积粘土(Q₁^al)相对隔水层组成，该地层在空间分布稳定、产状平缓，构成上覆风积中细砂孔隙潜水含水层近似水平的隔水底板(图 1，图 2).

图  1  古雷半岛水文地质简图

Fig.  1.  Hydrogeological sketch of Gulei peninsula

下载: 全尺寸图片 幻灯片

图  2  古雷半岛水文地质剖面

Fig.  2.  Hydrogeological profile of Gulei peninsula

下载: 全尺寸图片 幻灯片

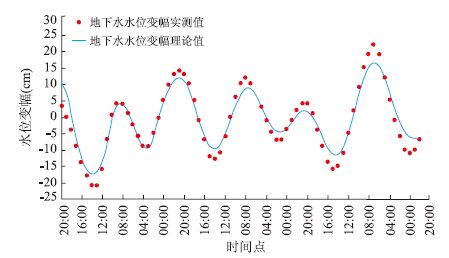
第四系全新统风积潜水含水层主要接受大气降雨入渗补给，由陆地向浮头湾径流排泄入海，由于补给范围有限，地下水潜水面极为平缓，水力坡度一般小于0.5%，地下水流向近似垂直海岸线，地下水水位埋深为2.0～5.0 m.笔者对当地民井调查发现，本区第四系风积潜水含水层的地下水水位动态受海水潮汐涨落影响呈现出周期性变化规律.为了更准确地掌握地下水潮汐效应的变化规律，笔者在距离海岸线100 m处埋置了Levelogger地下水自动观测仪，在2015年2月1～3日(大潮期间)开展了地下水水位动态监测，并同时监测了浮头湾海水潮汐动态，监测结果如图 3所示.

图  3  海水位及地下水水位变幅时间序列

Fig.  3.  Fluctuation of the tide and groundwater levels

下载: 全尺寸图片 幻灯片

从图 3中可见本区地下水水位呈现出与海水潮汐一致的非正规半日潮特征，即每天地下水水位也呈现出2个高潮和2个低潮的周期性变化特点，地下水最大波动幅度达0.38 m，最小波动幅度为0.11 m，地下水波动幅度约为海水波动幅度的1/10.地下水的波动周期约为12 h，地下水波动相对于海水波动有明显的滞后现象，滞后时间约为6 h.

1.2   海水潮汐特征及潮汐波动方程的确定

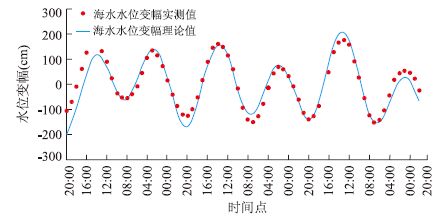
海水潮汐现象是由于海水在天体(主要是月球和太阳)引潮力作用下所产生的海平面的周期性运动现象.对于某一具体地区由于海、陆特征的差异其海水潮汐的微观特征(包括潮汐的周期、涨幅等)各不相同，在构建地下水潮汐效应的水文地质数学模型过程中必须掌握海水潮汐的特征及其数学描述.本次研究笔者对古雷半岛浮头湾海水潮汐进行了现场实测(图 3)，实测数据显示，本区海水呈非正规半日潮特点，即一天中有2次潮汐涨落，2次高潮位、2次低潮位(潮差不等)，监测期间海水最大潮差为3.15 m，最小潮差为1.81 m，每次波动波幅不等，周期为12 h.

以往地下水潮汐效应研究中一般都将海水潮汐用一个正弦或者余弦函数来表示海潮的波动，这对于半日潮的描述不尽合理，实际海潮往往是一个复杂的周期运动，并不是简单的正、余弦函数.

由Fourier变换原理可知任何连续测量的时序或信号，都可以表示为不同频率的余弦波信号的无限叠加.应用该原理，笔者可以将海水潮汐的波动方程用如下多个余弦函数叠加的形式表示：

式中，S_sea表示以平均海平面为基准的海水位波动幅度值(m)，A_j表示各谐波振幅(m)，ω_j表示各谐波角频率(rad/h)，φ_j表示各谐波相位(rad)，N表示谐波总个数，t表示观测时间，单位(h).

Fourier变换是信号处理的一个重要解决手段，它通过将数据序列从时域变换到频域，根据其频域分析组数据的周期特征.徐进军和魏静(2001)运用离散Fourier变换原理对潮汐数据进行频谱分析，确定该组数据的主要角频率.笔者通过频谱分析得到浮头湾潮汐数据的主要角频率按谐波能量由大到小依次为0.265 5、0.132 7、0.510 5、0.221 2、0.309 7和0.177 0 rad/h.

根据上述原理结合海潮波幅的实际观察资料，利用最小二乘法以海水水位波动幅度观测值为目标函数F₁，并结合MATLAB软件的参数估算功能，笔者编程计算了对应谐波的波幅和相位.

式中，S_i^m表示潮汐水位变幅计算理论值(m)，S_i^t表示潮汐水位变幅实测值(m)，N₁表示潮汐水位变幅观测数据个数.

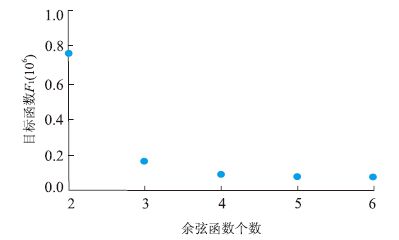
由海潮的基本特征，即2个高潮、2个低潮的特点，先选取2个余弦函数对其进行拟合，其角频率选取谐波能量最大时对应的2个角频率值，即0.265 5 rad/h和0.132 7 rad/h，依照此方法，按主要角频率对应谐波能量由大到小的顺序依次增加余弦函数个数，对潮汐数据进行拟合.拟合精度如图 4所示，当增加余弦函数个数为5时，其拟合精度相对余弦函数为4个时没有明显提高，因此笔者选取角频率为0.265 5、0.132 7、0.510 5和0.221 2 rad/h的4个谐波来拟合此次潮汐数据.

图  4  余弦函数个数-拟合精度

Fig.  4.  he cosine number function-fitting precision

下载: 全尺寸图片 幻灯片

根据拟合结果，本区海水潮汐波动过程可以近似由4个余弦波叠加而成，各余弦波的特征参数如表 1所示，拟合结果如图 5所示，根据图中拟合结果显示，拟合曲线能较好地拟合出海水水位.

表  1  海潮数据的谱分析及拟合结果

Table  Supplementary Table   The tide data of spectrum analysis and the fitting results

j	1	2	3	4
ωi(r/h)	0.132 7	0.221 2	0.265 5	0.510 5
Ai(m)	0.050 0	0.620 0	0.950 0	1.320 0
φi(r)	0.157 1	1.099 6	5.654 9	5.906 2

下载: 导出CSV 

| 显示表格

图  5  海水位变幅实测值与理论值对比

Fig.  5.  Tide amplitude of measured values compared with theoretical values

下载: 全尺寸图片 幻灯片

2.   潜水含水层地下水潮汐效应的数学模型

1950年以来，国内外许多学者对滨海地区含水层的水头波动进行了解析解研究，这些研究大多集中在承压含水层的研究(Li and Chen，1991; Sun，1997; Tang and Jiao，2001; Guo et al.，2007; Li et al.，2007a，2007b)，对潜水含水层的解析研究较少，这主要是因为随地下水水位变化潜水含水层的饱水带厚度一直不断变化，这给解析解求解带来一定困难.Erskine(1991)提出如果海水的波动幅度与潜水含水层饱和带厚度之比小于10%时，Jacob(1950)的单一承压含水层的解析式可以用于描述潜水含水层.根据前述对研究区水文地质条件的分析，其滨海潜水含水层地下水潮汐波动的水文地质概念模型为含水层为等厚、均质各向同性、隔水底板和初始水头近似水平、无降雨入渗和蒸发排泄的剖面二维非稳定流模型，当潮汐观测孔离海岸线一定距离，并满足裘布依假定(即等势面近于直立)时即可近似概化为剖面一维非稳定流模型.以海岸线为原点，海岸方向为x轴正方向，海洋方向为x轴负方向，其数学模型可以表示为：

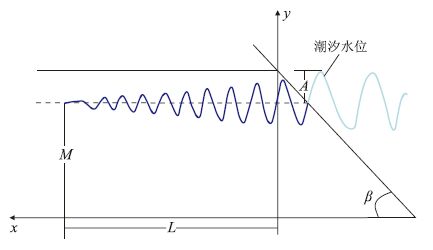
Nielsen(1990)提出当潮汐幅度与含水层受潮汐影响距离之比远小于海岸倾角的正弦值时(图 6)，即Acotβ/L＜＜1时，可以将滨海潜水含水层刻画为垂直海岸.

图  6  滨海含水层海岸线示意

Fig.  6.  Schematic of coastal aquifer coastline

下载: 全尺寸图片 幻灯片

图 6中L表示含水层受潮汐影响距离(m)，M表示含水层厚度(m)，β表示海岸坡度，A表示潮汐幅度(m).

因此，β=90°，该区可以用海水水位作为边界条件.

式中，S(0，t)表示潜水含水层在海岸线处的地下水位波幅值(m)，根据前文的研究S_sea表示海水潮汐的变幅函数表达式(式(5))，本区潮汐的变幅函数用4个余弦函数表示，式中参数取值见表 1.

参照Nielsen(1990)的求解方法，由以上方程组得滨海潜水含水层地下水水位波动方程为：

式中，S表示地下水位变幅值(m)，μ_d表示重力给水度；K是渗透系数(m/d)，M表示含水层厚度(m)，N表示谐波总个数，x表示陆地到海岸线距离(m)，D表示渗透系数与重力给水度的比值(m/d).

3.   含水层水文地质参数的识别

潜水含水层地下水水位波幅主要取决于海水潮汐波动及含水层结构和水文地质参数，若已知海水潮汐波动特征(即各谐波的参数)和含水层结构(含水层厚度M)，即可利用陆地地下水水位波动的序列观测资料来反演识别含水层的水文地质参数(渗透系数K与重力给水度μ_d的比值D)，具体方法如下：

以实测水位波幅与计算水位波幅误差最小为目标，运用最小二乘法，建立目标函数F₂.

式中，S_i^m表示观测孔中地下水水位变幅的理论值(m)，S_i^t表示观测孔中地下水水位变幅的理论值(m)，N₂表示观测孔中地下水水位降深值的个数.

笔者用MATLAB编程，不断优选渗透系数和给水度两个参数，直到目标函数F₂最小，由此得到的渗透系数K与重力给水度μ_d的比值D=206.77 m/d，将其代入式(8)中，可以得到此时地下水水位变幅的理论值，将其与实际观测值对比(图 7)可知，两者总体拟合较好，说明识别的参数比较理想.

图  7  观测孔地下水位变幅实测值与理论值对比

Fig.  7.  Groundwater level amplitude of measured values compared with theoretical values

下载: 全尺寸图片 幻灯片

笔者利用优选得到的参数，再代入地下水潮汐效应方程式(6)，并以地下水水位波幅小于1 cm作为潮汐效应的最小值，可以计算得到本区潜水含水层潮汐效应的影响距离是距海岸线L=300 m，这也与实地调查的结果基本吻合.

4.   结论

笔者通过对福建古雷半岛海水潮汐和潜水含水层水位动态监测发现，滨岸带潜水含水层地下水水位同样也受海水潮汐影响而呈现出周期性的变化规律，这种变化主要与海水潮汐波动特征、含水层结构和水文地质参数有关.

对研究区海水潮汐波动的监测表明，其海水波动具有半日潮的特征，不能简单地用1个余弦函数来表示，本文运用离散Fourier变换方法对海水潮汐进行了频谱分析，本区海水潮汐波动可以近似用4个谐波叠加表示.

根据研究区的水文地质条件建立了潜水含水层地下水水位波动的概念模型和数学模型，得到了该区地下水潮汐效应的波动方程式： $S\left( x,t \right)=-{{\sum }^{N}}_{j=1}{{A}_{j}}cos\left( {{\omega }_{j}}t-{{\varphi }_{j}}-\sqrt{\frac{{{\omega }_{j}}}{2DM}}x \right){{e}^{-\frac{{{\omega }_{j}}}{2DMx}}},$ ，依据该波动方程以地下水波幅序列观测值为目标函数，运用最小二乘法原理反演优化得到了其潜水含水层的渗透系数K与重力给水度μ_d的比值D=206.77 m/d，地下水受潮汐影响的范围L=300 m.