考虑初始损伤和残余强度的岩石变形过程模拟

温韬; 唐辉明; 马俊伟; 张俊荣; 范志强

doi:10.3799/dqkx.2018.212

考虑初始损伤和残余强度的岩石变形过程模拟

doi: 10.3799/dqkx.2018.212

温韬^1,,
唐辉明^1,2, ,,
马俊伟²,
张俊荣¹,
范志强¹

1.
中国地质大学工程学院, 湖北武汉 430074
2.
中国地质大学教育部长江三峡库区地质灾害研究中心, 湖北武汉 430074

基金项目:

项目编号

详细信息

作者简介:
温韬(1990-), 男, 博士生, 主要从事工程地质和岩土工程的研究.

通讯作者:
唐辉明

中图分类号: P589
计量
- 文章访问数: 5993
- HTML全文浏览量: 2539
- PDF下载量: 62
- 被引次数: 25
出版历程
- 收稿日期: 2018-05-05
- 刊出日期: 2019-02-15

Deformation Simulation for Rock in Consideration of Initial Damage and Residual Strength

1.
Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
2.
Three Gorges Research Center for Geohazards, Ministry of Education, China University of Geosciences, Wuhan 430074, China

摘要

摘要: 针对现有损伤模型的不足，提出同时反映岩石初始损伤和残余强度的岩石变形过程模拟方法.将岩石材料分为未损伤部分、损伤部分和微缺陷，未损伤部分和损伤部分共同承担岩石所受的应力.通过岩石材料几何条件及微观受力分析建立未损伤部分的应变分析.再考虑岩石的形变比能只与损伤部分材料相关，从而建立损伤部分的应变分析.然后探讨岩石损伤和耗散能的关系，提出了可以反映岩石初始损伤的损伤演化方程，基于各部分应变分析建立模拟岩石变形过程的损伤本构模型，同时给出模型各参数的确定方法.结果表明：损伤演化方程不仅表现了岩石的初始损伤特征，也可以完整地体现岩石变形破坏过程的5个阶段；与前人模型相比，提出的岩石变形模拟方法与试验曲线更加吻合，体现了岩石的变形全过程，特别是更加直观地反映了岩石的初始损伤和残余强度特征.综合体现了本文模型在模拟岩石变形全过程时的优势.
- 岩石 /
- 压密阶段 /
- 初始损伤 /
- 残余强度 /
- 本构模型
Abstract: Aiming at the limitations of previous rock damage constitutive models, a comprehensive simulation method of rock deformation to present simultaneously initial damage and residual strength is developed. With consideration of the initial damage of rock and the fact that the damage portion still can bear certain stress, deformation mechanism models of each portion are established by decomposing rock materials into three portions, undamaged material, damaged material and micro-defects. Firstly, on the basis of geometry conditions and micro-force for rocks, the strain analysis for undamaged material is proposed. Meanwhile, considering that the deformation energy of rock is only related to damaged material, the strain analysis for damaged material is developed. Then, discussing the relationships between damage evolution and energy dissipation, and putting forward a damage evolution model to reflect the initial damage for rocks, a rock damage constitutive model to simulate the complete processes of deformation for rocks is established based on the strain analysis and the determination methods of model parameters are also provided. The results show that damage evolution model not only reflects the initial damage for rocks, but also presents the rock deformation stages. Compared with previous models, the proposed damage constitutive model is more consistent with the experimental curve. In addition, the proposed model reflects the complete processes of deformation for rocks, and presents intuitively the characteristics of the initial damage and the residual strength. Thus, the superiority of the model is validated.
- rock /
- closure stage /
- initial damage /
- residual strength /
- constitutive model

HTML全文

岩石是一种自带损伤的地质材料，或多或少都存在微裂隙、微空洞等微细观缺陷，岩石变形破坏过程实际上就是微细观缺陷的形成、扩展到贯通的过程.损伤理论就是用来研究材料的变形破坏过程及微细观缺陷的形成演化过程.近年来，损伤力学在岩石工程领域得到了广泛应用，并取得了较好的成果，如分析岩石内部微裂纹的扩展过程；通过建立损伤演化方程探讨岩石的损伤过程；提出普适的损伤本构模型用于预测岩石的峰值强度和残余强度等.岩石损伤本构模型是建立岩体损伤本构模型的基础，对岩体的认识最早也是从岩石开始的，因此岩体损伤力学的很多概念与方法等都是从岩石损伤力学发展而来的.

随着计算机的发展，细观损伤力学得到了较好的发展，结合损伤理论，从全新的视角探讨了岩石的损伤演化(朱建明等, 2000; Peng et al., 2015a; Yang et al., 2015).还有学者考虑岩石本身存在的微缺陷具有随机性的特征，将岩石强度微元化，并假设其服从某种分布函数，提出了适用于不同条件的损伤模型(曹文贵等, 2004；曹文贵和张升，2005; 张珂等, 2016; Wen et al., 2017).杨圣奇等(2004)、杨明辉等(2005)分析所提出的模型参数和应力应变曲线的固有特征，提出了普遍适用的损伤参数确定方法.此外，学者对损伤变量的定义呈多样化，将轴向应力当成损伤变量(龚晓南, 2000; 胡黎明和濮家骝, 2002)；或选择模量作为损伤变量(范华林和金丰年, 2000)；或将岩石屈服准则作为损伤变量(吴二林等, 2013)，从而建立损伤本构模型.但是，这些损伤本构模型都有较明显的缺陷，忽视了岩石的初始损伤特性，岩石变形过程中的体积变化也无法体现.基于损伤的重新定义(曹文贵等, 2011; 温韬等, 2016a)，将岩石抽象为损伤材料、未损伤材料和空隙3部分，并基于统计理论建立岩石损伤统计本构模型，虽然较前人模型有更好的结果，但是基于统计理论建立的损伤演化方程仍无法反映岩石的初始损伤特性.后来曹文贵等(2016a, 2016b)将岩体材料分为空隙和骨架两部分，从岩石变形力学过程与力学机理来分析岩石的变形破坏，但是其未考虑岩石损伤部分仍能承受一定应力，认为损伤部分、未损伤部分的应变相协调，然而加载过程中岩石不断产生新的微裂纹，原生初始裂纹也将不断扩展、贯通甚至形成宏观裂纹，岩石中裂纹的尺寸和密度都将产生变化，相应地对岩石各部分变形非协调性产生新的影响，其建立的模型曲线与试验曲线仍有较大差距，且未考虑损伤部分与空隙之间的联系，仅将岩石材料分为空隙和骨架两部分研究欠妥，因此，有必要进一步完善基于损伤理论的岩石变形全过程的模拟研究.

本文采用宏细观结合的方法，对岩石未损伤部分、损伤部分和微缺陷部分均进行变形分析.通过探讨岩石损伤和耗散能的关系，提出考虑岩石初始损伤的损伤演化方程，并基于该演化方程和各部分应变分析建立岩石损伤本构模型，以期建立的模型可以表现岩石的初始损伤和残余强度特性.

1. 岩石材料变形分析模型

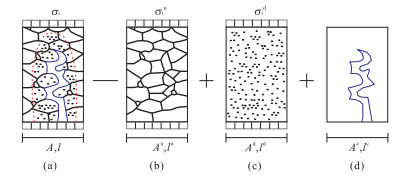
根据文献(温韬等，2016a)可知，岩石材料分为未损伤材料、损伤材料、微缺陷3部分，如图 1所示，并建立了基于应力分析的模型，而本文则从岩石变形分析的角度来建立岩石材料的变形分析模型.由于微缺陷部分由材料损伤导致，该部分虽然不受应力，但是在外力作用下，空隙、孔隙压缩产生变形，该部分变形产生的根本原因在于空隙发生闭合，而这种空隙的闭合必须在持续增大的应力作用下才能持续产生，而且空隙闭合产生的变形是不可恢复的，该类变形不能随应力的卸除而恢复，因此岩石受力情况下微缺陷部分仍会产生轴向应变ε₁^c.

图 1 含微缺陷的岩石损伤模型

a.损伤岩石材料；b.未损伤部分；c.损伤部分；d.微缺陷部分

Fig. 1. Rock damage model including micro-defects

下载: 全尺寸图片幻灯片

根据图 1所示岩石微观模型易知：

$l = {l^{\rm{u}}} + {l^{\rm{d}}} + {l^{\rm{c}}},$

(1)

式中：l为岩石长度；l^u为未受损伤部分长度；l^d为损伤部分长度；l^c为微缺陷部分长度，且l^c=γl^d，γ为影响因子，表征损伤材料与微缺陷部分的关系.

岩石材料在外力σ₁作用下将产生变形，变形量用Δl表示，其中未损伤部分变形量为Δl^u，损伤部分变形量为Δl^d，微缺陷部分变形量为Δl^c，则：

$\Delta l = \Delta {l^{\rm{u}}} + \Delta {l^{\rm{d}}} + \Delta {l^{\rm{c}}}.$

(2)

则岩石材料的轴向应变可表示为：

${\varepsilon _1} = \Delta l/l.$

(3)

此外，未损伤部分、损伤部分、微缺陷部分的轴向应变分别表示为：

$\left\{ \begin{array}{l} \varepsilon _{\rm{l}}^{\rm{u}} = \Delta {l^{\rm{u}}}/{l^{\rm{u}}}\\ \varepsilon _{\rm{l}}^{\rm{d}} = \Delta {l^{\rm{d}}}/{l^{\rm{d}}}\\ \varepsilon _{\rm{l}}^{\rm{c}} = \Delta {l^{\rm{c}}}/{l^{\rm{d}}} \end{array} \right.,$

(4)

式中：ε₁^u为未受损伤部分长度；ε₁^d为损伤部分长度；ε₁^c为微缺陷部分长度.

如果令l^c/l=δ，再综合式(1)~(4)可得岩石材料的轴向应变与其3部分各自的应变之间的关系式：

${\varepsilon _{\rm{l}}} = \left( {1 - \delta - \frac{\delta }{\gamma }} \right)\varepsilon _{\rm{l}}^{\rm{u}} + \frac{\delta }{\gamma }\varepsilon _{\rm{l}}^{\rm{d}} + \delta \varepsilon _{\rm{l}}^{\rm{c}},$

(5)

式(5)即为基于岩石变形分析的新型模型，从式(5)中可以看出，岩石材料的轴向应变ε₁与其3部分的应变(ε₁^u、ε₁^d、ε₁^c)不存在变形协调关系，这与实际更加符合.因此，本文模型比以前的模型更可靠.

为了进一步分析岩石材料的变形破坏过程，式(5)中的各部分变形计算是需要解决的问题.因此，本文提出以下解决思路.

1.1 未损伤部分的应变分析

岩石材料承受一维应力状态下，未损伤部分的应变独立于微缺陷的应变，通过几何条件及微观受力分析可知：

$A = {A^{\rm{u}}} + {A^{\rm{d}}} + {A^{\rm{c}}},$

(6)

${A^{\rm{c}}} = nA,$

(7)

${{\sigma }_{1}}A=\sigma _{1}^{\text{u}}{{A}^{\text{u}}}+\sigma _{1}^{\text{d}}{{A}^{\text{d}}},$

(8)

式中：A为岩石的受力面积；A^u为未损伤部分受力面积；A^d为损伤部分受力面积；A^c为微缺陷部分所占面积；σ₁^u为未损伤部分所受应力；σ₁^d为损伤部分所受应力；n为岩石空隙率，定义为岩石初始空隙面积及由损伤而形成的新空隙的面积之和占岩石材料总面积的比值.

此外，从材料受力面积的角度定义损伤变量为：

$D = \left( {{A^{\rm{d}}} + {A^{\rm{c}}}} \right)/A.$

(9)

综合式(6)~(9)可得：

${\sigma _1} = \left( {1 - n} \right)\left[ {\sigma _{\rm{l}}^u\left( {1 - D} \right) + \sigma _{\rm{l}}^dD} \right],$

(10)

式(10)即为损伤材料所受的名义应力.

由于σ₁^u是未损伤部分所受的应力，其符合广义虎克定律，则有：

$\varepsilon _{\rm{1}}^{\rm{u}} = \left[ {\sigma _{\rm{1}}^{\rm{u}} - {\mu _1}\left( {\sigma _{\rm{2}}^{\rm{u}} + \sigma _{\rm{3}}^{\rm{u}}} \right)} \right]/{E_1},$

(11)

式中ε₁^u为未损伤部分的应变；E₁和μ₁为岩石损伤部分材料的弹性模量及泊松比.

此外，弹性形状改变比能是由于岩石的形状改变产生的耗散能量，是由岩石损伤部分产生的，最终转变为摩擦耗散能；而空隙部分和未损伤部分的只会产生由岩石体积变化形成的体变比能，根据该条件和Mohr-Coulomb准则可得(曹文贵等, 2006)：

$\sigma _3^{\rm{d}} = k,$

(12)

$\sigma _1^{\rm{d}} = k{\tan ^2}\alpha + 2c\tan \alpha ,$

(13)

其中：

$\begin{array}{l} k = \\ \frac{{\left[ {\left( {1 + {\mu _2}} \right)\sigma _{\rm{c}}^2\sin \alpha /\left( {3{E_2}{\varepsilon _1}} \right) - c} \right]\cot \varphi - 2c\sin \alpha }}{{\sin \alpha \left( {1 + \tan \alpha } \right)}}, \end{array}$

(14)

$\alpha = \frac{{\rm{ \mathit{ π} }}}{4} + \frac{\varphi }{2},$

(15)

式中：c和φ分别是岩石的内聚力、内摩擦角.

因此，根据上述几式可得：

$\begin{array}{l} \varepsilon _{\rm{1}}^{\rm{u}} = \\ \frac{{{\sigma _1} - D\left( {1 - n} \right)\sigma _1^{\rm{d}} - {\mu _1}\left[ {{\sigma _2} + {\sigma _3} - D\left( {1 - n} \right)\left( {\sigma _2^{\rm{d}} + \sigma _3^{\rm{d}}} \right)} \right]}}{{\left( {1 - n} \right)\left( {1 - D} \right){E_1}}}. \end{array}$

(16)

因此得出了未损伤部分应变的求解公式，式中包括空隙率n、损伤变量D等参量，n体现了岩石变形过程中微缺陷的变化情况，而D揭示了岩石的损伤程度，二者结合更能反映岩石的损伤状态，从而体现岩石损伤的机制.而此公式的关键在于如何有效地确定空隙率和损伤变量.

1.2 损伤部分的应变分析

损伤部分的变形性质不同于未损伤部分和微缺陷部分，它的变形是由于岩石材料受力超过屈服强度引起的.为此，本文提供一种思路解决损伤部分的应变.

根据以前的研究(温韬等, 2016b)可知，岩石的变形可以分解为两部分：体积的变化和形状的变化，因此，在压缩条件下，应变能也可以由两部分组成：导致体积压缩的体变比能和导致变形的畸变比能，其中体变比能和畸变比能是相互独立的.考虑到常规三轴压缩实验先施加围压，然后再测量应变，该试验可以获得偏应力和偏应变之间的关系曲线.因此，认为由体积压缩引起的体变比能部分不会增加岩石的损伤，而岩石的形变比能只与损伤材料的变化相关，当弹性形变比能达到极限才会引起岩石损伤，岩石损伤后储存的形变比能也只由损伤部分材料内部的摩擦力消耗，可得：

${{U}^{\text{d}}}=\frac{{{\left( {{\sigma }_{1}}-{{\sigma }_{3}} \right)}^{2}}}{6G}=\frac{{{E}_{2}}\left( 1+{{\mu }_{2}} \right)}{3}{{\left( {{\varepsilon }_{1}} \right)}^{2}},$

(17)

其中G为剪切模量： $G = {\rm{ }}\frac{{{E_2}}}{{2\left( {1 + {\mu _2}} \right)}}$ .

首先将在Δσ_i^d应力下的应变增量为Δε_i^dt(t=1, 2, …, m)，其相对应的应变能增量为ΔU^dt，在常规三轴情况下，根据能量定理及应力应变曲线可知：

$\Delta {U^{{\rm{d}}t}} = \sigma _1^{\rm{d}}\Delta \varepsilon _1^{{\rm{d}}t} + \sigma _2^{\rm{d}}\Delta \varepsilon _2^{{\rm{d}}t} + \sigma _3^{\rm{d}}\Delta \varepsilon _3^{{\rm{d}}t}.$

(18)

将t份应变能增量ΔU^dt叠加，即对式(18)求和可得：

${U^{\rm{d}}} = \sigma _1^{\rm{d}}\varepsilon _1^{\rm{d}} + \sigma _2^{\rm{d}}\varepsilon _2^{\rm{d}} + \sigma _3^{\rm{d}}\varepsilon _3^{\rm{d}}.$

(19)

又根据常规三轴试验和损伤材料的泊松比可知|ε₃^d/ε₁^d|=μ₂，则联立式(17)和(19)可得：

$\varepsilon _1^{\rm{d}} = \frac{{\left( {1 + {\mu _2}} \right){{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}}}{{3{E_2}\left( {\sigma _1^{\rm{d}} + 2{\mu _2}\sigma _3^{\rm{d}}} \right)}} = \frac{{{E_2}\left( {1 + {\mu _2}} \right)\varepsilon _1^2}}{{3\left( {\sigma _1^{\rm{d}} + 2{\mu _2}\sigma _3^{\rm{d}}} \right)}}.$

(20)

由此就建立了损伤部分的应变分析方法.

1.3 微缺陷部分的应变分析

为了建立岩石材料在应力σ₁作用下微缺陷部分的应变ε₁^c，参考曹文贵等(2016a)的方法进行求解，可得微缺陷部分的应变：

$\varepsilon _1^c = 1 - \exp \left[ { - \frac{{{\sigma _1} - {\mu _3}\left( {{\sigma _2} + {\sigma _3}} \right)}}{{{E_3}}}} \right]$

(21)

根据前述分析得出了岩石各部分应变的表达式，因此将式(16)、(20)和(21)代入式(5)可得能够反映岩石变形破坏全过程的损伤本构模型，如下式(22)所示：

$\begin{array}{*{20}{c}} {{\varepsilon _1} = \left( {1 - \delta - \frac{\delta }{\gamma }} \right) \cdot }\\ {\left\{ {\frac{{{\sigma _1} - D\left( {1 - n} \right)\sigma _1^{\rm{d}} - {\mu _1}\left[ {{\sigma _2} + {\sigma _3} - D\left( {1 - n} \right)\left( {\sigma _2^{\rm{d}} + \sigma _3^{\rm{d}}} \right)} \right]}}{{\left( {1 - n} \right)\left( {1 - D} \right){E_1}}}} \right\} + }\\ {\frac{\delta }{\gamma }\left[ {\frac{{\left( {1 + {\mu _2}} \right){{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}}}{{3{E_2}\left( {\sigma _1^{\rm{d}} + 2{\mu _2}\sigma _3^{\rm{d}}} \right)}}} \right] + \delta \left\{ {1 - \exp \left[ { - \frac{{{\sigma _1} - {\mu _3}\left( {{\sigma _2} + {\sigma _3}} \right)}}{{{E_3}}}} \right]} \right\}.} \end{array}$

(22)

2. 参数确定方法

由式(22)可知，为了得出能够体现岩石变形过程的损伤本构模型曲线，仍需确定D、δ、γ、n、E₁、μ₁、E₂、μ₂、E₃、μ₃、等模型参数.这些参数无法直接通过常规试验获取，本文根据岩石的三轴压缩试验曲线来确定待定参数.

2.1 损伤变量D的确定

由于岩石材料内部存在许多微缺陷(如空隙裂隙)，即具有非均质性(王新刚等, 2016)，谢和平(1990)认为岩石产生损伤的两个影响因素：原始微缺陷的扩展和贯通；由于沿晶体界面的成核和晶体接头的断裂导致新的微缺陷产生.崔德山等(2016)认为试样内部微缺陷的不断扩展及演化等过程皆属于能量耗散以及非线性动力学机制.此外，谢和平(1990)提出了岩石损伤变量与耗散能间的关系式，如下所示：

$D = 1 - \exp \left( { - \lambda {{\left| {{U^{\rm{d}}} - U_0^{\rm{d}}} \right|}^\beta }} \right),$

(23)

式中：λ和β是与材料性质相关的参数；U^d是引起岩石损伤所需的耗散能；U^d < U₀^d是与岩石初始损伤相对应的耗散能，根据式(23)初始损伤耗散能(U₀^d)与初始损伤变量(D₀)是一一对应的.

然而式(23)中存在绝对值，且初始加载时U^d < U₀^d，不能满足该指数函数成立的条件，参数λ和β无法确定，导致岩石的损伤演化过程无法求解，因此，田洪铭等(2012)忽略初始损伤的影响，将式(23)简化为：

$D = 1 - \exp \left[ { - \lambda {{\left( {{U^{\rm{d}}}} \right)}^\beta }} \right].$

(24)

以前的损伤变量基本都通过统计损伤理论确定，假设岩石微元强度符合概率分布函数，包括正态分布、Weibull分布、对数正态分布.如曹文贵等(2016a)引入统计损伤理论，基于Weibull分布提出了岩石材料的损伤演化模型：

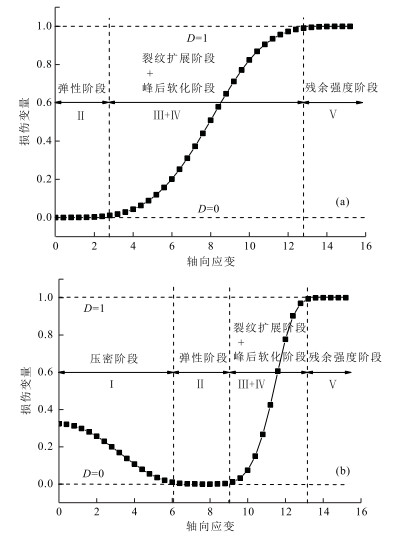
$D = \left\{ {\begin{array}{*{20}{c}} {1 - \exp \left[ { - {{\left( {F/{F_0}} \right)}^m}} \right],F \ge 0}\\ {0,F < 0} \end{array}} \right..$

(25)

从式(24)和(25)可知，式(24)的损伤演化方程形式与曹文贵等(2016a)提出的统计损伤演化模型一样.从上述公式得出以下结论：初始加载时岩石的损伤变量为0，在应力作用下岩石完全破坏对应的损伤变量为1，从开始加载至岩石完全破坏的过程中，岩石的损伤演化曲线是单调递增的，如图 2a所示，但由该损伤模型建立的岩石损伤本构模型不能描述岩石的峰后应力降和残余阶段特征.

图 2 压缩情况下典型的岩石损伤演化曲线

a.前人的理论曲线；b.本文的理论曲线

Fig. 2. Typical rock damage curves under loading conditions

下载: 全尺寸图片幻灯片

根据压缩情况下岩石的应力应变曲线，岩石变形过程划分为5个阶段：空隙裂隙压密阶段、弹性阶段、裂纹扩展阶段、峰后软化阶段和残余阶段.在以往的研究中，阶段Ⅰ的损伤演化过程往往忽略不计，但是由于岩石样本中存在许多原始的空隙裂隙，因此阶段Ⅰ的损伤演化过程事实上是存在的，不能被忽略.

损伤变量是用来描述岩石受荷变形过程中损伤程度的相对值，选取不同的损伤起始点(D=0)将会得到不同的损伤演化过程.大多数情况下，取应力为0时岩石的损伤变量为损伤起始点，由于损伤变量不可能为负，损伤变量只能随着压缩过程的进行逐渐增大，这样建立的损伤演化过程不能合理描述岩石的压密过程.因此，本文选取弹性变形阶段时的损伤变量为损伤起始点，即岩石处于弹性变形阶段时损伤变量为0，根据裂隙体积应变的演化规律，岩石的损伤程度在压密过程逐渐减小，经过弹性变形阶段后在裂隙发育阶段逐渐增大.

通过研究岩石的损伤演化过程可知，基于统计损伤理论求解损伤变量的表达式存在不妥之处，不能描述岩石的峰后应力降和残余阶段特征，有必要对其进行改进.因此，提出了一种新的损伤演化方程：

$D = 1 - \exp \left\{ { - \lambda \left| {{{\left[ {\left( {{U^{\rm{d}}} - U_0^{\rm{d}}} \right)/{U_0}} \right]}^{2\beta }}} \right|} \right\},$

(26)

其中U₀为单位应变能，取值为1 mJ/(mm)³.

文中所建立的损伤演化方程与应变能(U^d)相关，而为了描述这一损伤变量在裂隙压密阶段处的演化过程，文中引入了初始损伤耗散能这一变量(U₀^d)，这样就有了文中所建立的损伤变量演化过程.根据式(26)绘制岩石的损伤演化曲线，见图 2b.在岩石空隙裂隙的压缩过程中，张开的空隙裂隙逐渐地闭合，导致岩石的有效力承载面积增加.由式(26)可知，在空隙裂隙压密阶段，应变逐渐增加，损伤变量反而减小.可知岩石还未承受外力时，由于存在原始的空隙裂隙，初始损伤变量必然大于0.但是对于密度较大的岩石(花岗岩、大理岩等)，因为其应力应变曲线并没有明显的Ⅰ阶段，因此初始损伤变量可看作0.在岩石的弹性变形阶段，应力应变曲线上表现为线性，因此岩石的损伤变量等于0.这个阶段岩石原始的空隙裂隙处于压实状态并且还未形成新的裂隙.当处于裂纹扩展阶段时，损伤变量随着应变的增加呈非线性增加，伴随着新裂隙的形成、扩展及贯通.当岩石进入残余阶段，损伤变量达到1并趋于稳定.

图 2a展示了岩石材料基于Weibull分布得出的统计损伤演化曲线，很明显该演化曲线不能反映岩石的空隙裂隙压密阶段.图 2b展示了岩石材料基于能量理论得出的损伤演化曲线，该演化曲线能够更好地描述岩石的全过程曲线，包括5个阶段.

2.2 δ的确定

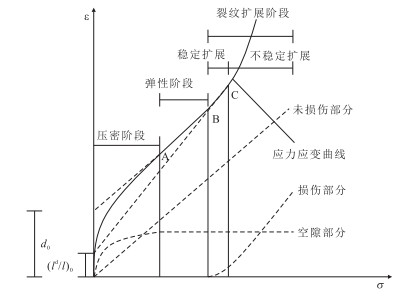
根据l^c/l=δ可知参数δ表示某一时刻微缺陷部分长度占总长度的比值.岩石的峰前变形分为3个阶段(彭俊等, 2015)：裂纹压密阶段；弹性阶段；裂纹扩展阶段，这3个阶段分别以裂纹闭合应力、岩石起裂应力和岩石峰值强度为分界点，而裂纹扩展阶段以损伤应力为界线可以分为裂纹稳定扩展阶段和裂纹不稳定扩展阶段.当岩石进入弹性阶段时，空隙裂隙已处于闭合状态，即可认为微缺陷部分的变形已达到最大值δ₀，因此，取岩石压缩试验曲线上弹性线段延长至应变轴上，此时对应的截距即为δ₀，如图 3所示，未损伤部分材料变形先为线弹性后为非线性，损伤部分变形仅当岩石强度超过屈服强度时产生，并呈现非线性特征，空隙部分材料变形始终为非线性且逐渐趋于稳定.

图 3 岩石各部分之间的变形关系

Fig. 3. Deformation relationships among each portion of rock

下载: 全尺寸图片幻灯片

2.3 γ的确定

根据l^c=γl^d和l^c/l=δ可以得出：

$\gamma = \delta /\left( {{l^d}/l} \right).$

(27)

由于l^d/l表示某一时刻损伤部分长度占总长度的比值，因此，γ的求解可以转化为对损伤部分材料变形的极限值，假设岩石在压密阶段和弹性阶段都无损伤，岩石的损伤开始于裂纹扩展阶段，该阶段岩石内部裂纹处于不稳定状态，此时的损伤应力表示岩石的长期强度(Diederichs et al., 2004).当轴向应力增加到岩石损伤应力时，应力应变曲线进入裂纹不稳定扩展阶段，这也是岩石出现剪胀现象的节点，岩石的体积应变开始从压缩向扩容转变，此时，l^d/l值已达到一个临界点，因此，将试验曲线在该应力下的切线延长至应变轴上，此时对应的截距即为(l^d/l)₀.综上所述，可知γ的取值为γ=δ₀(l^d/l)₀.

2.4 空隙率n的确定

对于空隙率n的变化关系，引用文献(曹文贵等, 2011)方法可知：

$\begin{array}{l} n = 1 - \\ \frac{{\left( {1 - {n_0}} \right)\left( {1 - D} \right) + {P_1}{\sigma _3}}}{{{P_2}{\varepsilon _1} + 1 + D\left( {{P_3}/{\varepsilon _1} - {P_2}{\varepsilon _1} - {P_4} - 1} \right)}}, \end{array}$

(28)

其中：

${P_1} = 2\left( {1 - {\mu _2} - 2\mu _2^2} \right)/{E_2},$

(29)

${P_2} = 2{\mu _2} - 1,$

(30)

${P_3} = {P_1}\left( {1 + {\mu _2}} \right)\sigma _c^2\cot \varphi /\left[ {3\left( {1 + \tan \alpha } \right){E_2}} \right],$

(31)

${P_4} = {P_1}c\left( {\cot \varphi + 2\sin \alpha } \right)/\left[ {\sin \alpha \left( {1 + \tan \alpha } \right)} \right].$

(32)

2.5 E₁和μ₁的确定

E₁是未损伤部分的弹性模量, 本文取弹性阶段的直线斜率为E₁, μ₁也通过该弹性段求取.

2.6 E₃的确定

基于有效介质理论，假设在空隙裂隙闭合阶段，应力应变曲线上任一点的应变可分为基质轴向应变和裂纹轴向应变，即：

${\varepsilon _1} = \varepsilon _1^{\rm{m}} + \varepsilon _1^{\rm{c}}.$

(33)

而基质轴向应变与岩石内部裂隙闭合后的弹性模量是线性相关的，表示为：

$\varepsilon _1^{\rm{m}} = \frac{{{\sigma _1}}}{E},$

(34)

其中：E为岩石的弹性模量.

因此，岩石的裂纹轴向应变可表示为：

$\varepsilon _1^{\rm{c}} = {\varepsilon _1} - \frac{{{\sigma _1}}}{E}.$

(35)

通过式(35)可得出裂纹轴向应变的变化曲线，并通过下述公式进行拟合可得E₃和μ₁：

$\varepsilon _1^{\rm{c}} = 1 - \exp \left[ { - \frac{{{\sigma _1} - {\mu _3}\left( {{\sigma _2} + {\sigma _3}} \right)}}{{{E_3}}}} \right].$

(36)

2.7 E₂和μ₂的确定

对于常规三轴试验，由于岩石的偏应力-应变曲线不包含轴向应力加载至围压所产生的应变.因此，根据试验曲线确定模型参数需要考虑该影响.当加载至围压时，满足σ₁=σ₂=σ₃.此时，根据式(22)可得岩样被加载至围压时所产生的初始轴向应变ε_c, 即

$\begin{array}{*{20}{c}} {{\varepsilon _{\rm{c}}} = \left( {1 - \delta - \frac{\delta }{\gamma }} \right)\left[ {\frac{{\left( {1 - 2{\mu _1}} \right){\sigma _1} - D\left( {1 - n} \right)\sigma _1^{\rm{d}} + 2{\mu _1}D\sigma _3^{\rm{d}}\left( {1 - n} \right)}}{{\left( {1 - n} \right)\left( {1 - D} \right){E_1}}}} \right]}\\ { + \delta \left\{ {1 - \exp \left[ { - \frac{{\left( {1 - 2{\mu _3}} \right){\sigma _1}}}{{{E_3}}}} \right]} \right\}} \end{array}.$

(37)

因此，试验获得实际应变ε₁^′应为：

${{\varepsilon '}_1} = {\varepsilon _1} - {\varepsilon _{\rm{c}}}.$

(38)

结合式(37)和式(38)可得：

$\begin{array}{l} {{\varepsilon '}_1} = \left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}\left( {{\sigma _1} - {\sigma _3}} \right)}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \frac{{\delta \left( {1 + {\mu _2}} \right){{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} + \\ \delta \left\{ {\exp \left[ { - \frac{{\left( {1 - 2{\mu _3}} \right){\sigma _1}}}{{{E_3}}}} \right] - \exp \left( { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right)} \right\}. \end{array}$

(39)

当岩石加载进入弹性阶段时空隙压密变形已完成，即式(39)等式右边第3项为常数，因此根据式(39)求出应力应变曲线上直线段AB的斜率，可表示为：

$\begin{array}{l} {k_{AB}} = \partial \left( {{\sigma _1} - {\sigma _3}} \right)/\partial {{\varepsilon '}_1} = \\ \frac{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}}{{2{\mu _1}}}\left( {1 - \delta - \frac{\delta }{\gamma }} \right) + \frac{{2\gamma \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\delta {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}}. \end{array}$

(40)

在偏应力-应变曲线弹性阶段，假设(σ₁－σ₁)_A,(σ₁－σ₁)_B, ε₁^A和ε₁^B分别为直线段起始点A和终点B所对应的偏应力和应变，则有：

${k_{AB}} = \left[ {{{\left( {{\sigma _1} - {\sigma _3}} \right)}_A} - {{\left( {{\sigma _1} - {\sigma _3}} \right)}_B}} \right]/\left( {\varepsilon _1^A - \varepsilon _1^B} \right).$

(41)

综合式(40)和(41)可得：

${{E}_{2}}=\frac{2\gamma \left( 1+{{\mu }_{2}} \right)\left( {{\sigma }_{1}}-{{\sigma }_{3}} \right)}{3\delta \left( \sigma _{1}^{d}+2{{\mu }_{2}}\sigma _{3}^{d} \right)\left\{ \left[ {{\left( {{\sigma }_{1}}-{{\sigma }_{2}} \right)}_{A}}-{{\left( {{\sigma }_{1}}-{{\sigma }_{3}} \right)}_{B}} \right]/\left( \varepsilon _{1}^{A}-\varepsilon _{1}^{B} \right)-\frac{{{E}_{1}}\left( 1-n \right)\left( 1-D \right)}{2{{\mu }_{1}}}\left( 1-\delta -\frac{\delta }{\gamma } \right) \right\}}.$

(42)

仅由式(42)可知，仍然无法同时确定E₂和μ₂，必须建立另一个等式才能进行求解.

又因为损伤部分在裂纹扩展阶段之前皆无损伤，损伤开始于裂纹稳定扩展阶段，临界点在应力应变曲线上表现在岩石的损伤应力处.在偏应力-应变曲线上，假设(σ₁－σ₁)_c，和ε₁^C分别为损伤强度点C所对应的偏应力和应变，对于常规三轴试验，当岩石强度达到损伤强度时，偏应力应变曲线在该点的斜率可表示为：

${k_{\rm{C}}} = \frac{{\partial \left( {{\sigma _1} - {\sigma _3}} \right)}}{{\partial {{\varepsilon '}_1}}}.$

(43)

当岩石强度达到损伤强度时围压已处于定值，此时的实际应变如式(39)所示，对式(39)两边取微分，可得：

$\begin{array}{l} {\rm{d}}{{\varepsilon '}_1} = \left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}\left( {{\rm{d}}{\sigma _1} - {\rm{d}}{\sigma _3}} \right)}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \\ \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)\left( {{\rm{d}}{\sigma _1} - {\rm{d}}{\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} - \\ \frac{{\delta \left( {1 - 2{\mu _3}} \right)}}{{{E_3}}}\exp \left[ { - \frac{{\left( {1 - 2{\mu _3}} \right){\sigma _1}}}{{{E_3}}}} \right]{\rm{d}}{\sigma _1} + \frac{\delta }{{{E_3}}}\exp \left( - \right.\\ \left. {\frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right)\left( {{\rm{d}}{\sigma _1} - 2{\mu _3}{\rm{d}}{\sigma _3}} \right). \end{array}$

(44)

对上式进行化简，可得：

$\begin{array}{l} {\rm{d}}{{\varepsilon '}_1} = \left[ {\left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + } \right.\\ \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} - \frac{{\delta \left( {1 - 2{\mu _3}} \right)}}{{{E_3}}}\exp \left( { - \frac{{\left( {1 - 2{\mu _3}} \right){\sigma _1}}}{{{E_3}}}} \right) + \\ \left. {\frac{\delta }{{{E_3}}}\exp \left( { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right)} \right]{\rm{d}}{\sigma _1} - \left[ {\left( {1 - \delta - \frac{\delta }{\gamma }} \right) \cdot } \right.\\ \frac{{2{\mu _1}}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} + \\ \left. {\frac{{2\delta {\mu _3}}}{{{E_3}}}\exp \left( { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right)} \right]{\rm{d}}{\sigma _3}. \end{array}$

(45)

由导数的运算法则可知，式(43)可变为：

$\frac{{\partial \left( {{\sigma _1} - {\sigma _3}} \right)}}{{\partial {\varepsilon _1}}} = \frac{{\partial {\sigma _1}}}{{\partial {\varepsilon _1}}} - \frac{{\partial {\sigma _3}}}{{\partial {\varepsilon _1}}}.$

(46)

联立式(45)和(46)可得：

$\begin{array}{l} {k_{\rm{C}}} = \frac{1}{{\left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} - \frac{{\delta \left( {1 - 2{\mu _3}} \right)}}{{{E_3}}}\exp \left[ { - \frac{{\left( {1 - 2{\mu _3}} \right){\sigma _1}}}{{{E_3}}}} \right] + \frac{\delta }{{{E_3}}}\exp \left( { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right)}} - \\ \frac{1}{{\left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} + \frac{{2\delta {\mu _3}}}{{{E_3}}}\exp \left( { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right).}} \end{array}$

(47)

由于在确定参数γ时，已知应力应变曲线上损伤强度点的切线的延长线与应变轴的截距为(l^d/l)₀，因此可得：

${k_{\rm{C}}} = {\left( {{\sigma _1} - {\sigma _3}} \right)_{\rm{c}}}/\left[ {\varepsilon _1^{\rm{C}} - {{\left( {{l^{\rm{d}}}/l} \right)}_0}} \right].$

(48)

联立式(47)和(48)，可求得岩石损伤部分的弹性模量E₂和泊松比μ₂之间的另一个关系式：

$\begin{array}{l} \frac{1}{{\left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} - \frac{{\delta \left( {1 - 2{\mu _3}} \right)}}{{{E_3}}}\exp \left[ { - \frac{{\left( {1 - 2{\mu _3}} \right){\sigma _1}}}{{{E_3}}}} \right] + \frac{\delta }{{{E_3}}}\exp \left[ { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right]}}\\ - \frac{1}{{\left( {1 - \delta - \frac{\delta }{\gamma }} \right)\frac{{2{\mu _1}}}{{{E_1}\left( {1 - n} \right)\left( {1 - D} \right)}} + \frac{{2\delta \left( {1 + {\mu _2}} \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{3\gamma {E_2}\left( {\sigma _1^d + 2{\mu _2}\sigma _3^d} \right)}} + \frac{{2\delta {\mu _3}}}{{{E_3}}}\exp \left( { - \frac{{{\sigma _1} - 2{\mu _3}{\sigma _3}}}{{{E_3}}}} \right)}} = \left( {_{\sigma 1}/\left[ {\varepsilon _1^{\rm{C}} - \left( {{{_l}^{\rm{d}}}} \right.} \right]} \right.. \end{array}$

(49)

综上所述，联立式(42)、(49)便能求得岩石损伤部分的弹性模量和泊松比.

3. 模型求解步骤

根据前面的分析，本文提出的岩石损伤本构模型应重点集中于公式(22)的解决过程.由于该本构模型具有高度非线性的特点，因此必须通过迭代程序得以计算.解决步骤如下：

(1) 首先根据式(26)求解损伤变量D，建立实时损伤演化模型；

(2) 根据不同围压下的屈服强度和峰值强度，基于Mohr-Coulomb准则通过线性拟合确定计算所需的抗剪强度参数c与φ；

(3) 文中所提参数δ和γ的求解；

(4) 空隙率n的求解；

(5) 岩石变形参数(E₁、μ₁、E₂、μ₂、E₃、μ₃)的求解；

(6) 将上述求解的D、δ、γ、n、E₁、μ₁、E₂、μ₂、E₃、μ₃代入式(22)，得出一个方程，将该方程中的轴向应变视为未知量，而轴向应力视为从试验数据中获取的已知量；

(7) 将试验所测的轴向应变作为参考值，然后通过迭代程序获取预测的轴向应变值，当误差在一个很小的允许范围内，就将该值视为预测的轴向应变值，然后将该预测值与试验测量值进行对比.

4. 实例与验证

前面已建立了考虑初始损伤的本构模型并给出了模型各参数的确定方法，但其实用性仍有待验证.因此，引入文献(Fairhurst and Hudson, 1999)中Xingan矿煤岩的常规三轴压缩试验进行探讨，共计4组围压(5、10、20和30 MPa)，首先需要通过上述参数确定方法确定相关参数(表 1~4).

表 1 不同围压下确定损伤模型所需的参数

Table Supplementary Table The damage model parameters under different confining pressures

σ₃(MPa)	ε₁⁰(10^-3)	γ	β	U₀^d(mJ/mm³)	R²
5	2.61	9.92×10^-8	1.48	137.69	0.99
10	1.80	3.55×10^-6	1.03	154.62	0.99
20	1.87	6.88×10^-8	1.27	270.68	0.99
30	1.78	9.55×10^-20	3.39	466.80	0.99

下载: 导出CSV

| 显示表格

表 2 不同损伤变量对应的强度参数值

Table Supplementary Table The strength parameters corresponding to different damage variables

D	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
φ(°)	36.65	37.82	36.73	35.48	34.13	32.77	31.31	29.73	28.02	26.29	24.10
c(MPa)	7.72	6.55	5.89	4.95	4.77	4.67	4.60	4.47	4.40	4.26	4.19

下载: 导出CSV

| 显示表格

表 3 不同围压下的δ和γ的值

Table Supplementary Table The values of δ and γ under different confining pressures

σ₃(MPa)	5	10	20	30
δ(10^-3)	2.448	1.721	1.411	1.277
γ	2.194	1.387	1.084	1.722

下载: 导出CSV

| 显示表格

表 4 岩石各部分的变形参数

Table Supplementary Table Mechanical parameters of each portion of rock

σ₃(MPa)	E₁(GPa)	μ₁	E₂(GPa)	μ₂	E₃(MPa)	μ₃
5	2.502	0.14	2.085	0.23	1.133	0.47
10	3.377	0.16	2.598	0.25	1.634	0.47
20	3.657	0.18	2.709	0.26	1.643	0.48
30	3.75	0.19	2.778	0.26	1.681	0.49

下载: 导出CSV

| 显示表格

4.1 损伤变量的求解

根据4组围压下煤岩的测试结果，可以获取煤岩的损伤模型参数，其中各围压下材料参数γ和β的值通过式(24)拟合得出，如表 1所示.

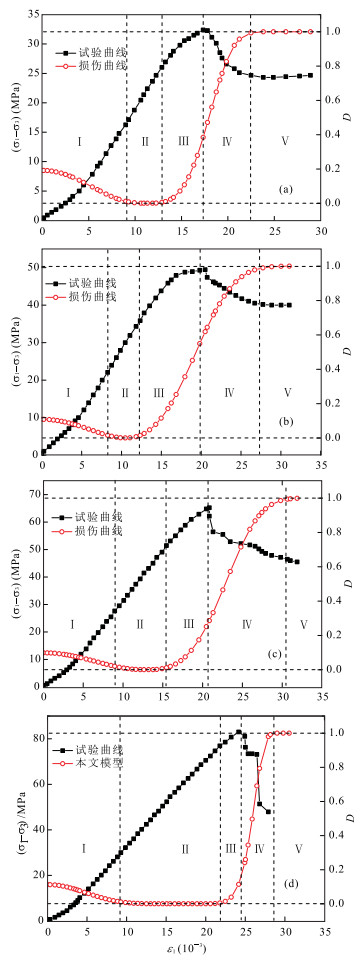
图 4展示了4组围压下煤岩的损伤演化曲线，依据本文模型得出的损伤演化曲线可以与岩石变形破坏过程一一对应.损伤演化曲线初始的减小阶段对应着应力应变曲线的向上凹部分，是岩石变形破坏的压密阶段，以裂纹闭合应力为临界点.损伤演化曲线中D=0部分对应着应力应变曲线的直线段，该直线段对应的初始应力和末端应力分别是裂纹闭合应力和裂纹起裂应力，是岩石变形破坏的弹性阶段，以裂纹起裂应力为临界点.损伤演化曲线中向上凹部分对应着应力应变曲线上弹性阶段末端应力至峰值强度这一部分，是岩石变形破坏的裂纹扩展阶段，以峰值应力为临界点.损伤演化曲线中向上凸部分对应着应力应变曲线上峰值强度至残余强度这一部分，是岩石变形破坏的峰后软化阶段，以残余强度为临界点.损伤演化曲线中D=1部分对应的是应力应变曲线上的峰后稳定阶段，表明已达到残余阶段.

图 4 岩石损伤演化曲线

a.σ₃=5 MPa; b.σ₃=10 MPa; c.σ₃=20 MPa; d.σ₃=30 MPa

Fig. 4. Rock damage evolution curves

下载: 全尺寸图片幻灯片

至此，确定了岩石变形过程的实时损伤变量，再将实时损伤变量代入本文提出的损伤本构模型.

4.2 强度参数的求解

本文模型的建立需要在强度指标(包括内聚力和摩擦角)已知的条件下进行，前人模型均通过多种围压条件下拟合得到岩石的强度指标，并认为岩石的强度指标在岩石的变形破坏过程中是不变的，且不同围压下其强度指标相同，这与实际情况是相悖的(胡政等, 2014)，不同的变形阶段岩石的强度参数也不同，并随着加载的进行，岩石强度参数会发生劣化，因此，本文通过每个围压下的三轴试验数据得出多组强度指标，通过建立其与损伤变量的关系式，得出岩石强度指标随岩石变形破坏过程的变化规律，这样就建立了强度指标的实时演化方程，再代入损伤本构模型中求解，就能获得更符合实际的模型.

由于σ₁和σ₃在Mohr-Coulomb准则中是线性关系(σ₁=kσ₃+b)，可以通过回归获得不同损伤变量对应的强度参数值，计算方法如下：

$\left. \begin{array}{l} \varphi = \arcsin \left( {\frac{{k - 1}}{{k + 1}}} \right)\\ c = \frac{{b\left( {1 - \sin \varphi } \right)}}{{2\cos \varphi }} \end{array} \right\}.$

(50)

根据上式，得出不同损伤变量下的强度参数值，如表 2所示.

从表 2可知损伤变量及其所对应的强度参数值，通过绘制损伤变量-强度参数曲线，得出它们之间的拟合关系，如式(51)所示，将该拟合公式应用于损伤本构模型中，得出模型曲线：

$\left. \begin{array}{l} \varphi = - 13.578D + 38.883,\;\;\;{R^2} = 0.958\;4\\ c = 5.331\;7{D^2} - 8.278\;3D + 7.407\;6,\;\;\;{R^2} = 0.953\;8 \end{array} \right\}.$

(51)

4.3 文中所提参数的求解

根据上述δ和γ的确定方法，可得不同围压下δ和γ的值，如表 3所示.

4.4 变形参数和空隙率的求解

本文的变形参数包括E₁、μ₁、E₂、μ₂、E₃、μ₃，根据第4节内容确定这些变形参数，然后根据式(28)就可以求出不同损伤变量下的空隙率n，变形参数值如表 4所示.

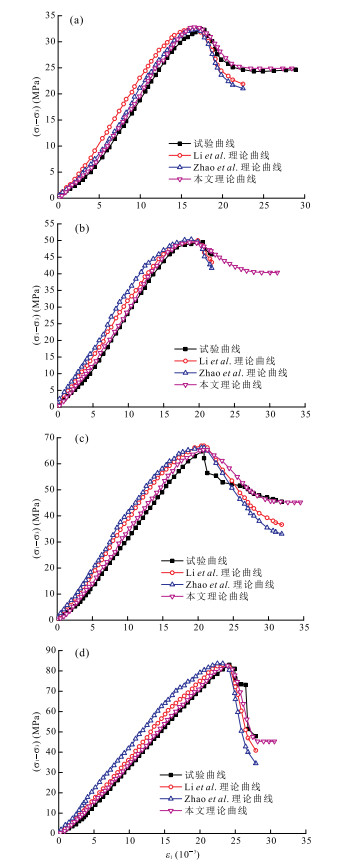
待上述模型参数都获取后，代入式(22)可得本文所提的不同围压下模拟岩石变形过程的模型曲线，为了进一步说明本文所提模型的可行性及合理性，文中加入文献(Li et al., 2012; Zhao et al., 2016)的模型进行对比，得出它们的模型理论曲线，如图 5所示.与Li et al.(2012)模型和Zhao et al.(2016)模型相比，本文模型与试验曲线的吻合度明显更好，更能体现岩石变形破坏的全过程，特别是在初始压密阶段和残余强度阶段优势明显，反映了压密阶段的非线性特征和残余强度特征，可用于预测不同围压下岩石的残余强度.

图 5 试验曲线与理论曲线的比较

a.σ₃=5 MPa; b.σ₃=10 MPa; c.σ₃=20 MPa; d.σ₃=30 MPa

Fig. 5. The comparison of experimental curves and theoretical curves

下载: 全尺寸图片幻灯片

5. 结论

(1) 采用宏细观结合的方法，将岩石分为未损伤部分、损伤部分和微缺陷3部分，通过岩石材料几何条件及微观受力分析建立未损伤部分的应变分析，再考虑岩石的形变比能只与损伤材料的变化相关及应力应变曲线建立损伤部分的应变分析.

(2) 在岩石各部分变形分析的基础上，引入损伤理论，提出了可以反映岩石初始损伤及变形阶段的损伤演化模型，并提出了模拟岩石变形全过程的损伤本构模型，此外，给出了模型各待定参数的确定方法.

(3) 通过与前人模型对比，表明本文模型在描述岩石变形全过程中具有优势，特别是更直观地反映了岩石的初始损伤和残余强度特性，此外本文得出的损伤演化过程更符合实际，表明了所提模型的优越性.

图 1 含微缺陷的岩石损伤模型

a.损伤岩石材料；b.未损伤部分；c.损伤部分；d.微缺陷部分

Fig. 1. Rock damage model including micro-defects

下载: 全尺寸图片幻灯片

图 2 压缩情况下典型的岩石损伤演化曲线

a.前人的理论曲线；b.本文的理论曲线

Fig. 2. Typical rock damage curves under loading conditions

下载: 全尺寸图片幻灯片

图 3 岩石各部分之间的变形关系

Fig. 3. Deformation relationships among each portion of rock

下载: 全尺寸图片幻灯片

图 4 岩石损伤演化曲线

a.σ₃=5 MPa; b.σ₃=10 MPa; c.σ₃=20 MPa; d.σ₃=30 MPa

Fig. 4. Rock damage evolution curves

下载: 全尺寸图片幻灯片

图 5 试验曲线与理论曲线的比较

a.σ₃=5 MPa; b.σ₃=10 MPa; c.σ₃=20 MPa; d.σ₃=30 MPa

Fig. 5. The comparison of experimental curves and theoretical curves

下载: 全尺寸图片幻灯片

表 1 不同围压下确定损伤模型所需的参数

Table 1. The damage model parameters under different confining pressures

σ₃(MPa)	ε₁⁰(10^-3)	γ	β	U₀^d(mJ/mm³)	R²
5	2.61	9.92×10^-8	1.48	137.69	0.99
10	1.80	3.55×10^-6	1.03	154.62	0.99
20	1.87	6.88×10^-8	1.27	270.68	0.99
30	1.78	9.55×10^-20	3.39	466.80	0.99

下载: 导出CSV

表 2 不同损伤变量对应的强度参数值

Table 2. The strength parameters corresponding to different damage variables

D	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
φ(°)	36.65	37.82	36.73	35.48	34.13	32.77	31.31	29.73	28.02	26.29	24.10
c(MPa)	7.72	6.55	5.89	4.95	4.77	4.67	4.60	4.47	4.40	4.26	4.19

下载: 导出CSV

表 3 不同围压下的δ和γ的值

Table 3. The values of δ and γ under different confining pressures

σ₃(MPa)	5	10	20	30
δ(10^-3)	2.448	1.721	1.411	1.277
γ	2.194	1.387	1.084	1.722

下载: 导出CSV

表 4 岩石各部分的变形参数

Table 4. Mechanical parameters of each portion of rock

σ₃(MPa)	E₁(GPa)	μ₁	E₂(GPa)	μ₂	E₃(MPa)	μ₃
5	2.502	0.14	2.085	0.23	1.133	0.47
10	3.377	0.16	2.598	0.25	1.634	0.47
20	3.657	0.18	2.709	0.26	1.643	0.48
30	3.75	0.19	2.778	0.26	1.681	0.49

下载: 导出CSV

参考文献(51)

Cao W.G., Zhang C., He M., et al.2016a.Deformation Simulation of Brittle Rock Based on Micromechanical Properties.Rock and Soil Mechanics, 37(10):2753-2760(in Chinese with English abstract). http://d.old.wanfangdata.com.cn/Periodical/ytlx201610003
Cao W.G., Zhang C., He M., et al.2016b.Statistical Damage Simulation Method of Strain Softening Deformation Process for Rocks Considering Characteristics of Void Compaction Stage.Chinese Journal of Geotechnical Engineering, 38(10):1754-1761(in Chinese with English abstract). http://d.old.wanfangdata.com.cn/Periodical/ytgcxb201610002
Cao W.G., Zhang S..2005.Study on the Statistical Analysis of Rock Damage Based on Mohr-Coulomb Criterion.Journal of Hunan University (Natural Sciences), 32(1):43-47(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hndxxb200501010
Cao W.G., Zhang S., Zhao M.H..2006.Study on Statistical Damage Constitutive Model of Rock Based on New Definition of Damage.Rock and Soil Mechanics, 27(1):41-46(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-YTLX200601007.htm
Cao W.G., Zhao H., Zhang Y.J., et al.2011.Strain Softening and Hardening Damage Constitutive Model for Rock Considering Effect of Volume Change and Its Parameters Determination Method.Rock and Soil Mechanics, 32(3):647-654(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ytlx201103002
Cao W.G., Zhao M.H., Liu C.X..2004.Study on the Model and Its Modifying Method for Rock Softening and Damage Based on Weibull Random Distribution.Chinese Journal of Rock Mechanics and Engineering, 23(19):3226-3231(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb200419003
Cui D.S., Xiang W., Chen Q., et al.2016.Experiment of Energy Dissipation and Energy Release during Stick-Slip within Glass Beads.Earth Science, 41(9):1603-1610(in Chinese with English abstract). http://d.old.wanfangdata.com.cn/Periodical/dqkx201609015
Diederichs M.S., Kaiser P.K., Eberhardt E..2004.Damage Initiation and Propagation in Hard Rock during Tunnelling and the Influence of Near-Face Stress Rotation.International Journal of Rock Mechanics and Mining Sciences, 41(5):785-812. https://doi.org/10.1016/j.ijrmms.2004.02.003
Fairhurst C.E., Hudson J.A..1999.Draft ISRM Suggested Method for the Complete Stress-Strain Curve for Intact Rock in Uniaxial Compression.International Journal of Rock Mechanics and Mining Sciences, 36(3):279-289. https://doi.org/10.1016/S0148-9062(99)00006-6
Fan H.L., Jin F.N..2000.Effective Modulus Method in Damage Mechanics of Rock.Chinese Journal of Rock Mechanics and Engineering, 19(4):432-435(in Chinese with English abstract). http://www.cqvip.com/Main/Detail.aspx?id=4334429
Gong X.N..2000.Prospects for the Development of Geotechnical Engineering in the 21th Century.Chinese Journal of Geotechnical Engineering, 22(2):238-242(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTotal-YTGC200002019.htm
Hu L.M., Pu J.L..2002.Damage of Soil-Structure Interface.Rock and Soil Mechanics, 23(1):6-11(in Chinese with English abstract). http://d.old.wanfangdata.com.cn/Periodical/ytlx201802021
Hu Z., Liu Y.R., Wu S., et al.2014.Experimental Study of Deformation Parameters Degradation of Sandstone in High Geostress Regions under Unloading Conditions.Rock and Soil Mechanics, 35(Suppl.1):78-84(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-YTLX2014S1011.htm
Li X., Cao W.G., Su Y.H..2012.A Statistical Damage Constitutive Model for Softening Behavior of Rocks.Engineering Geology, 143-144:1-17. https://doi.org/10.1016/j.enggeo.2012.05.005
Peng J., Cai M., Liu D.Q., et al.2015a.A Phenomenological Model of Brittle Rocks under Uniaxial Compression.International Journal of Geohazards and Environment, 1(2):53-62.https://doi.org/10.1016/j.enggeo.2015.12.011 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e00f7462fe3053a9caaa5bdca6d8962a
Peng J., Cai M., Rong G., et al.2015b.Stresses for Crack Closure and Its Application to Assessing Stress-Inducing Microcrack Damage.Chinese Journal of Rock Mechanics and Engineering, 34(6):1091-1100(in Chinese with English abstract). http://www.jstor.org/stable/41666839
Tian H.M., Chen W.Z., Tian T., et al.2012.Experimental and Theoretical Studies of Creep Damage Behavior of Soft Rock.Chinese Journal of Rock Mechanics and Engineering, 31(3):610-617(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb201203020
Wang X.G., Hu B., Tang H.M., et al.2016.Triaxial Rheological Experiments and Rheological Constitutive of Mudstone under Hydro-Mechanical Coupling State.Earth Science, 41(5):886-894(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqkx201605014
Wen T., Liu Y.R., Yang C.G., et al.2017.A Rock Damage Constitutive Model and Damage Energy Dissipation Rate Analysis for Characterising the Crack Closure Effect.Geomechanics and Geoengineering, 13(1):54-63.https://doi.org/10.1080/17486025.2017.1330969 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/17486025.2017.1330969
Wen T., Tang H.M., Liu Y.R., et al.2016a.Newly Modified Damage Statistical Constitutive Model of Rock Based on Impact Factor.Journal of China University of Mining & Technology, 45(1):141-149(in Chinese with English abstract). http://d.old.wanfangdata.com.cn/Periodical/zgkydxxb201601019
Wen T., Tang H.M., Liu Y.R., et al.2016b.Energy and Damage Analysis of Slate during Triaxial Compression under Different Confining Pressures.Coal Geology & Exploration, 44(3):80-86(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=mtdzykt201603015
Wu E.L., Wei C.F., Wei H.Z., et al.2013.A Statistical Damage Constitutive Model of Hydrate-Bearing Sediments.Rock and Soil Mechanics, 34(1):60-65(in Chinese with English abstract). http://d.wanfangdata.com.cn/Periodical/ytlx201301009
Xie H.P..1990.Damage Mechanics of Rock and Concrete.China University of Mining & Technology Press, Xuzhou, 173-186(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/slfdxb201106007
Yang M.H., Zhao M.H., Cao W.G..2005.Method for Determining the Parameters of Statistical Damage Softening Constitutive Model for Rock.Journal of Hydraulic Engineering, 36(3):345-349(in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slxb200503015
Yang S.Q., Xu P., Ranjith P.G..2015.Damage Model of Coal under Creep and Triaxial Compression.International Journal of Rock Mechanics and Mining Sciences, 80:337-345. https://doi.org/10.1016/j.ijrmms.2015.10.006
Yang S.Q., Xu W.Y., Wei L.D., et al.2004.Statistical Constitutive Model for Rock Damage under Uniaxial Compression and Its Experimental Study.Journal of Hohai University (Natural Sciences), 32(2):200-203(in Chinese with English abstract). http://www.cqvip.com/Main/Detail.aspx?id=9392062
Zhang K., Liu, S.Wei C.Y., et al.2016.Constitutive Model and Damage Evolution of Rock under Different Loads.Journal of Shenyang Jianzhu University (Natural Science), 32(5):896-903(in Chinese with English abstract).
Zhao H., Shi C.J., Zhao M.H., et al.2016.Statistical Damage Constitutive Model for Rocks Considering Residual Strength.International Journal of Geomechanics, 17(1):04016033.https://doi.org/10.1061/(asce)gm.1943-5622.0000680 http://cn.bing.com/academic/profile?id=524bcc2b4e181af69c67a75b190ea7a6&encoded=0&v=paper_preview&mkt=zh-cn
Zhu J.M., Xu B.Y., Ren T.G., et al.2000.Establishing the Damage Evolution Equation of the Fractured Rocks Based on the Triaxial Compression Tests.Journal of Engineering Geology, 8(2):175-179(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-GCDZ200002008.htm
曹文贵, 张超, 贺敏, 等.2016a.基于微观力学特性的脆性岩石变形过程模拟.岩土力学, 37(10):2753-2760. http://d.old.wanfangdata.com.cn/Periodical/ytlx201610003
曹文贵, 张超, 贺敏, 等.2016b.考虑空隙压密阶段特征的岩石应变软化统计损伤模拟方法.岩土工程学报, 38(10):1754-1761. http://d.old.wanfangdata.com.cn/Periodical/ytgcxb201610002
曹文贵, 张升.2005.基于Mohr-Coulomb准则的岩石损伤统计分析方法研究.湖南大学学报(自然科学版), 32(1):43-47. doi: 10.3321/j.issn:1000-2472.2005.01.010
曹文贵, 赵衡, 张永杰, 等.2011.考虑体积变化影响的岩石应变软硬化损伤本构模型及参数确定方法.岩土力学, 32(3):647-654. doi: 10.3969/j.issn.1000-7598.2011.03.002
曹文贵, 张升, 赵明华.2006.基于新型损伤定义的岩石损伤统计本构模型探讨.岩土力学, 27(1):41-46. doi: 10.3969/j.issn.1000-7598.2006.01.008
曹文贵, 赵明华, 刘成学.2004.基于Weibull分布的岩石损伤软化模型及其修正方法研究.岩石力学与工程学报, 23(19):3226-3231. doi: 10.3321/j.issn:1000-6915.2004.19.003
崔德山, 项伟, 陈琼, 等.2016.细颗粒粘滑运动的能量耗散与释放试验.地球科学, 41(9):1603-1610. http://earth-science.net/WebPage/Article.aspx?id=3365
范华林, 金丰年.2000.岩石损伤定义中的有效模量法.岩石力学与工程学报, 19(4):432-435. doi: 10.3321/j.issn:1000-6915.2000.04.008
龚晓南.2000.21世纪岩土工程发展展望.岩土工程学报, 22(2):238-242. doi: 10.3321/j.issn:1000-4548.2000.02.020
胡黎明, 濮家骝.2002.土与结构物接触面损伤本构模型.岩土力学, 23(1):6-11. doi: 10.3969/j.issn.1000-7598.2002.01.002
胡政, 刘佑荣, 武尚, 等.2014.高地应力区砂岩在卸荷条件下的变形参数劣化试验研究.岩土力学, 35(增刊1):78-84. http://d.old.wanfangdata.com.cn/Periodical/ytlx2014z1011
彭俊, 蔡明, 荣冠, 等.2015.裂纹闭合应力及其岩石微裂纹损伤评价.岩石力学与工程学报, 34(6):1091-1100. http://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201506002.htm
田洪铭, 陈卫忠, 田田, 等.2012.软岩蠕变损伤特性的试验与理论研究.岩石力学与工程学报, 31(3):610-617. doi: 10.3969/j.issn.1000-6915.2012.03.020
王新刚, 胡斌, 唐辉明, 等.2016.渗透压-应力耦合作用下泥岩三轴流变实验及其流变本构.地球科学, 41(5):886-894. http://earth-science.net/WebPage/Article.aspx?id=3302
温韬, 唐辉明, 刘佑荣, 等.2016a.影响因子修正的新型岩石损伤统计本构模型.中国矿业大学学报, 45(1):141-149. http://d.old.wanfangdata.com.cn/Periodical/zgkydxxb201601019
温韬, 唐辉明, 刘佑荣, 等.2016b.不同围压下板岩三轴压缩过程能量及损伤分析.煤田地质与勘探, 44(3):80-86. http://d.old.wanfangdata.com.cn/Periodical/mtdzykt201603015
吴二林, 韦昌富, 魏厚振, 等.2013.含天然气水合物沉积物损伤统计本构模型.岩土力学, 34(1):60-65. http://d.old.wanfangdata.com.cn/Periodical/ytlx201301011
谢和平.1990.岩石、混凝土损伤力学, 徐州:中国矿业大学出版社, 173-186.
杨明辉, 赵明华, 曹文贵.2005.岩石损伤软化统计本构模型参数的确定方法.水利学报, 36(3):345-349. doi: 10.3321/j.issn:0559-9350.2005.03.015
杨圣奇, 徐卫亚, 韦立德, 等.2004.单轴压缩下岩石损伤统计本构模型与试验研究.河海大学学报(自然科学版), 32(2):200-203. doi: 10.3321/j.issn:1000-1980.2004.02.019
张珂, 刘帅, 魏春雨, 等.2016.岩石在不同应力条件下的本构模型与损伤演化.沈阳建筑大学学报(自然科学版), 32(5):896-903. http://cdmd.cnki.com.cn/Article/CDMD-10611-2009148286.htm
朱建明, 徐秉业, 任天贵, 等.2000.基于三轴压缩试验的破裂岩损伤演化方程的建立.工程地质学报, 8(2):175-179. doi: 10.3969/j.issn.1004-9665.2000.02.008

施引文献

期刊类型引用(15)

1.	刘冬桥，郭允朋，凌凯，李杰宇. 基于Logistic函数的层状砂岩单轴压缩全过程损伤本构模型（英文）. Journal of Central South University. 2024(07): 2411-2430 . 百度学术
2.	张根宝，张超，白允，杨楚卿. 空隙岩石非线性变形细观唯象分析及本构模型. 公路交通科技. 2023(02): 135-144 . 百度学术
3.	寇昊，何川，陈子全，周子寒，蒙伟，肖龙鸽. 考虑残余强度的层状岩体损伤演化规律. 西南交通大学学报. 2023(05): 1064-1072 . 百度学术
4.	宋昊，夏敏，任光明. 基于峰前能量演化及峰后侧向变形特征的岩石脆性评价方法. 成都理工大学学报(自然科学版). 2023(06): 723-733 . 百度学术
5.	茹文凯，胡善超，李地元，马金银，张晨曦，罗平框，弓昊，周奥辉. 煤岩组合体卸围压能量演化规律及耗散能损伤本构模型研究. 岩土力学. 2023(12): 3448-3458 . 百度学术
6.	陈会官，赵程，张睿，潘昊宇. 考虑空隙压密特征的岩石弹塑性损伤增量本构模型. 岩石力学与工程学报. 2023(12): 3043-3055 . 百度学术
7.	张超，曹文贵，赵衡，贺敏. 考虑围压效应和强度脆性跌落的岩石全应力–应变曲线统计损伤模拟方法. 岩土工程学报. 2022(05): 936-944 . 百度学术
8.	严孝海，郭长宝，刘造保，王炀，刘冬桥，刘贵. 四川康定某深埋隧道花岗岩岩爆物理模拟实验研究. 地球科学. 2022(06): 2081-2093 . 本站查看
9.	刘新锋，赵英群，王晓睿，于怀昌. 岩石疲劳损伤及破坏前兆研究现状与展望. 地球科学. 2022(06): 2190-2198 . 本站查看
10.	潘有维，黄德文. 考虑压密过程和残余强度的岩石统计损伤本构模型. 采矿技术. 2021(04): 38-42 . 百度学术
11.	温韬，张馨，孙金山，贾永胜，郎珉，贾文君，李德成，孙莉霞，唐辉明. 基于峰前和峰后能量演化特征的岩石脆性评价. 地球科学. 2021(09): 3385-3396 . 本站查看
12.	张超，雷勇，曹文贵. 考虑软硬物质双变形特征的脆性岩石损伤本构模型研究. 应用力学学报. 2020(03): 1166-1171+1397-1398 . 百度学术
13.	莫云龙，李宏艳，邓志刚，齐庆新，李海涛，张广辉. 不同冲击倾向性煤能量响应初始损伤效应分析. 采矿与安全工程学报. 2020(06): 1205-1212 . 百度学术
14.	蒲诚，刘奉银，陈蕴生. 非贯通裂隙岩体试件峰后力学特性的研究. 实验力学. 2020(06): 1121-1128 . 百度学术
15.	张慧梅，孟祥振，彭川，杨更社，叶万军，申艳军，刘慧. 冻融-荷载作用下基于残余强度特征的岩石损伤模型. 煤炭学报. 2019(11): 3404-3411 . 百度学术

其他类型引用(10)

资源附件(0)

访问统计

点击查看大图

图(5) / 表(4)

计量

文章访问数: 5993
HTML全文浏览量: 2539
PDF下载量: 62
被引次数: 25

1. 岩石材料变形分析模型
1.1 未损伤部分的应变分析
1.2 损伤部分的应变分析
1.3 微缺陷部分的应变分析
2. 参数确定方法
2.1 损伤变量D的确定
2.2 δ的确定
2.3 γ的确定
2.4 空隙率n的确定
2.5 E1和μ1的确定
2.6 E3的确定
2.7 E2和μ2的确定
3. 模型求解步骤
4. 实例与验证
4.1 损伤变量的求解
4.2 强度参数的求解
4.3 文中所提参数的求解
4.4 变形参数和空隙率的求解
5. 结论

1. 岩石材料变形分析模型
1.1 未损伤部分的应变分析
1.2 损伤部分的应变分析
1.3 微缺陷部分的应变分析
2. 参数确定方法
2.1 损伤变量D的确定
2.2 δ的确定
2.3 γ的确定
2.4 空隙率n的确定
2.5 E₁和μ₁的确定
2.6 E₃的确定
2.7 E₂和μ₂的确定
3. 模型求解步骤
4. 实例与验证
4.1 损伤变量的求解
4.2 强度参数的求解
4.3 文中所提参数的求解
4.4 变形参数和空隙率的求解
5. 结论

参考文献(51)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

考虑初始损伤和残余强度的岩石变形过程模拟

doi: 10.3799/dqkx.2018.212

作者简介: 温韬(1990-), 男, 博士生, 主要从事工程地质和岩土工程的研究.

通讯作者: 唐辉明

计量

出版历程

Deformation Simulation for Rock in Consideration of Initial Damage and Residual Strength

1. 岩石材料变形分析模型

1.1 未损伤部分的应变分析

1.2 损伤部分的应变分析

1.3 微缺陷部分的应变分析

2. 参数确定方法

2.1 损伤变量D的确定

2.2 δ的确定

2.3 γ的确定

2.4 空隙率n的确定

2.5 E1和μ1的确定

2.6 E3的确定

2.7 E2和μ2的确定

3. 模型求解步骤

4. 实例与验证

4.1 损伤变量的求解

4.2 强度参数的求解

4.3 文中所提参数的求解

4.4 变形参数和空隙率的求解

5. 结论

期刊类型引用(15)

其他类型引用(10)

计量

出版历程

目录

1. 岩石材料变形分析模型

1.1 未损伤部分的应变分析

1.2 损伤部分的应变分析

1.3 微缺陷部分的应变分析

2. 参数确定方法

2.1 损伤变量D的确定

2.2 δ的确定

2.3 γ的确定

2.4 空隙率n的确定

2.5 E1和μ1的确定

2.6 E3的确定

2.7 E2和μ2的确定

3. 模型求解步骤

4. 实例与验证

4.1 损伤变量的求解

4.2 强度参数的求解

4.3 文中所提参数的求解

4.4 变形参数和空隙率的求解

5. 结论

作者简介:
温韬(1990-), 男, 博士生, 主要从事工程地质和岩土工程的研究.

通讯作者:
唐辉明

2.5 E₁和μ₁的确定

2.6 E₃的确定

2.7 E₂和μ₂的确定

2.5 E₁和μ₁的确定

2.6 E₃的确定

2.7 E₂和μ₂的确定