Intelligent Interpretation of Rock Mass Discontinuity Based on Three-Dimensional Laser Point Cloud
-
摘要: 准确、高效、全面获取岩体结构面信息，对岩体的稳定性分析有着重要的意义.采用三维激光扫描设备进行岩体数据采集，基于岩体点云模型提出了结构面自动识别方法.通过对Ransac算法进行改进，引入了新的采样方法和评分准则，大大提升了Ransac算法的计算效率和提取精度，使之更好地适应粗糙不平的岩体点云数据；基于改进的Graham Scan算法可以精准描绘出结构面的凸凹边界，进而精细化计算出结构面尺寸.基于以上算法研发了结构面识别程序RDD（ransac discontinuity dtection），并且采用了两组标准几何体数据和一组岩体数据对程序进行测试.结果表明，标准几何体产状误差在1°以内，实际岩体最大误差在6°以内，结构面尺寸最大误差率为0.278%，满足工程限定的误差要求.
-
关键词:
- 三维激光点云 /
- 结构面 /
- Ransac算法 /
- Graham Scan算法 /
- 工程地质
Abstract: The stability of rock mass is mainly controlled by a large number of internal discontinuities. Therefore, the accurate and efficient extraction of discontinuity information is a significant process to analyze the stability of rock mass. In the paper, the raw point cloud data is collected by three-dimensional laser scanner, a new approach about automatic extraction of discontinuity is proposed based on point cloud model of rock mass, which can automatically decipher the parameters of rock mass discontinuities. The new sampling method and evaluation method are successfully introduced based on the modified Ransac algorithm, the efficiency and accuracy of Ransac algorithm are rapidly improved to adapt rough point cloud data of rock mass. The modified Graham Scan algorithm is proposed to delineate the convex-concave boundary and to calculate the size for discontinuity. Based on the above algorithms, this paper developed a discontinuity extraction program named RDD (ransac discontinuity dtection). RDD is tested by two sets of standard geometry data and one set of rock mass data. The results indicate that the orientation error of standard geometry is less than 1ånd the maximum error of rock is less than 6°, which satisfy the prescriptive error requirements of engineering. -
0. 引言
岩体工程的研究涉及水利工程、土木工程、边坡工程、隧道工程、采矿工程等多个领域. 研究表明，结构面的空间展布状态不仅控制了岩体的力学性质，而且在很大程度上决定了岩体的稳定性(谷德振，1979；孙广忠，1993). 因此，准确、有效地获取结构面信息是分析岩体稳定性的关键环节. 在实际工程中，传统的岩体信息采集方式有人工现场接触测量法、钻孔法(黄达和钟助，2015；汪进超等，2017；袁广祥等，2017). 人工现场接触测量利用罗盘、皮尺对岩体进行近距离测量，在作业环境缓和区域虽然能够全面、准确地采集信息，但在高陡边坡条件下使用会受到限制且存在安全隐患；钻孔法对钻孔技艺、成孔质量的要求较为特殊，且无法获得大规模岩体表面信息(于天亮，2009). 随着测量技术的进步，又发展出了近景摄影测量(范留明和李宁，2005；王明常等, 2018, 亢金涛等，2019；林松等，2019)和三维激光扫描(董秀军和黄润秋，2006；陈致富等，2012；邱俊玲等，2012)等新型测量手段，尤其是三维激光扫描技术，能够远距离高精度扫描实物并快速进行逆向模型重建，在岩体工程领域的应用越来越广泛(Warburton et al., 2004；Deb et al., 2007；Math et al., 2011；Tang et al., 2012；Lato et al., 2013；Li et al., 2019).
目前，基于三维点云模型识别岩体结构面的研究日益增多. 其中最简单的一种方法的是在结构面上人工至少选择3个点，根据这3个点计算出平面法向量，获取结构面参数信息. 但是这种方法属于人工方法，不仅效率低，而且存在风险. 第二种是通过识别点云顶点的主曲率变化或者在数字模型中搜索最佳平面来提取(Slob et al., 2005, 2007；Gigli and Casagli, 2010；Lato et al., 2012). 比如，Gigli and Casagli(2010)通过立方体搜索共面的点云子集，用最小二乘法进行平面拟合，然后合并邻近的Cluster得到同一结构面的点集，从而提取出结构面. 但是该方法计算结果对立方体的尺寸非常敏感，如果太大会将非结构面的点包含进来，如果太小，会忽略结构面上的点. Olariu et al.(2008)提出了一种基于原始点云的数据聚类方法来确定结构面组的平均产状. 虽然该方法功能强大，但是所提方法只是对所有结构面进行统计分组，无法识别出具体的单个结构面. 第三种是通过赤平投影将三角网格单元的法向量聚类到一个TIN网格模型中来提取(Vöge et al., 2013；Chen et al., 2016；Ge et al., 2018；Zhang et al., 2018). 比如，Ge et al.(2018)从创建的点云网格数据中挑选出种子点，通过设置种子点和相邻点的夹角阈值识别出点簇，从而实现了岩体结构面几何参数的半自动提取. Chen et al.(2016)利用点簇数目k值对结构面集合进行分组，通过RANSAC算法实现随机取样，并进行平面拟合，进而提取出结构面. 然而，这样的方法有两点不足：第一，三角网格化后会损失一部分点云，在描述物体表面细节上有些失真；第二，当点云数据离散点较多，或者点云数据处于封闭状态时，三角网格化的过程会产生较多的误差，甚至会出现许多畸形三角形.
针对以上岩体结构面信息提取方法的不足，本文提出了一种基于三维激光点云技术智能获取结构面参数信息的方法，该方法能够从原始点云数据中提取出岩体结构面，并通过对Ransac(random sample consensus discontinuity detection)算法的改进，成功引入了新的采样方法和评分准则，大幅度提升了Ransac算法对粗糙不平的岩体点云数据的计算效率和提取精度；同时，基于改进的Graham Scan算法对结构面的凹凸边界进行高精度描绘，从而计算出结构面的产状和等效尺寸. 另外，本文基于所提方法，研发了结构面自动识别程序Ransac discontinuity detection(RDD)，该程序可以基于原始点云识别结构面的特征点集，实现从岩体点云数据到结构面几何参数的智能解译.
1. 岩体结构面参数智能解译
1.1 法向量计算
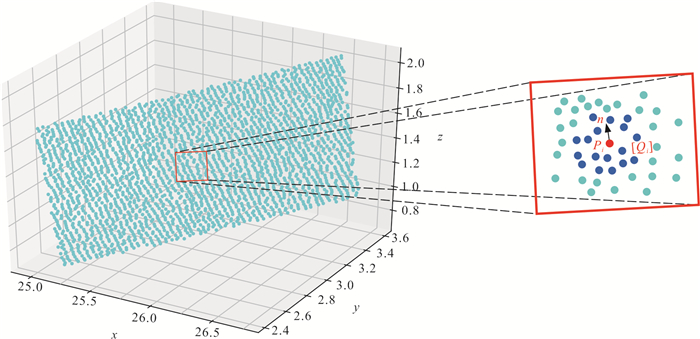
如图 1所示，假设{P}是一个原始点云集，Pi是{P}中的一个点，[Qi]是{P}的相邻点集，可计算出[Qi]的最佳拟合平面，从而计算出Pi的法向量.
图 1 [Qi]是Pi的近邻点集，n是Pi的法向量Fig. 1. Qi is the subset of Pi, n is the normal vector of Pi本文基于Kd⁃tree来搜索某点的K个最邻近点，从而创建邻近点集，通过分析邻近点集的协方差矩阵特征向量和特征值(或PCA⁃主成分分析)来估计表面法线. 具体而言，每个点Pi对应的协方差矩阵C满足：
C=1k∑ki=1×(pi−ˉp)×(pi−ˉp)T,C×→Vj=λj×→Vj,j∈{0,1,2}, (1) 此处：K是Pi邻近点的数量；$ \bar{p}$表示点集的三维质心；λj是该协方差矩阵的特征值；$ \vec{V}$j是它的特征向量，法向量可通过对应于它的最小的特征值的特征向量来确定.
1.2 基于改进的Ransac算法的岩体结构面提取
Ransac是一种电脑迭代算法，该算法通过随机选取一个子集样本来确定预定义的数学模型的参数，然后计算出所有点到这个模型的距离，通过设定阈值来筛选内点和外点，每一次迭代将会记录下内点的数量，最终内点数量最多的模型将会被视为最优模型(Uherčík et al., 2010). Ransac算法在二维数据中的简单应用如图 2所示. 图 2a中有一个包含内点和外点的点集，图 2b是Ransac算法的提取结果，其中蓝色线是由红色内点拟合得到的直线数学模型点.
对于岩体结构面提取(数学模型是平面)，Ransac算法有两个优点：(1)可直接应用于原始点云数据，无需三角网格化；(2)Ransac有很强的鲁棒性，能够处理超过50%的外点. 基于以上优点，许多研究人员试图将Ransac用于平面或结构面提取. 然而，由于点的数量较多，大多数算法的效率较低. 因此，本文采用了一种改进的Ransac算法，可大大提高算法的精度和速度.
1.2.1 改进的Ransac算法概述
给定一个点云集P={P1，…，PN}和所有点的法向量N={n1，…，nN}，输出结果是平面模型的一系列参数Ψ={Ψ1，…，ΨN}. 本文采用局部抽样法在每次迭代测试中获取新的候选平面，然后通过Ransac算法确定得分最高的平面模型(内点数最多)参数. 将所有的候选平面都被放置在集合C中，采用一种新的计算方法来计算出最佳平面的得分m. |m|是候选平面中点的数量，|c|是候选平面的数量，P(|m|，|c|)为忽略得分更高的平面的概率. 当P(|m|，|c|)足够大时，所提取的候选平面为最佳平面，剩余点将用于下一轮迭代运算. 当P(τ，|c|)足够大时，整个迭代过程将会终止，τ(用户自定义)是平面中的最少的点个数. 伪代码如下表所示.
Algorithm 1 基于改进的Ransac算法提取平面Supplementary Table Extract plane based on modified Ransac algorithmInput: P is a matrix which stores the point cloud. Output #1：Ψ is a matrix which stores the parameters of the extracted discontinuities.
Output #2：Pψ is a matrix which stores the points belonging to the corresponding discontinuities.
1：Ψ←Φ{extracted discontinuities}
2：C ←Φ{discontinuities candidates}
3: repeat
4: C ← C ∪ new candidates ()
5: m←best candidate(C)
6: if P(|m|, |c|)＞pt then
7: P ← P\Pm {remove points}
8: Ψ←Ψ ∪ m
9: C←C\Cm {remove invalid candidates}
10: end if
11: until P(τ, |c|)＞pt
12: return Ψ1.2.2 概率计算
给定一个有N个点的点云集和一个有n个点的平面，k是确定一个平面的最小的点云集中点的数量. 如果假定任何含有k个点的子集都将生成一个平面模型，那么在一次迭代运算中检测出平面Ψ的概率是：
P(n)=(nk)/(Nk)≈(nN)k, (2) 当S个待选平面已经被检测出来后，检测出平面Ψ的概率是：
p(n,S)=1−[1−p(n)]S. (3) 人为设定一个阈值，通过求解S可以得到满足要求的平面的数量T：
T⩾ln(1−Pt)ln[1−p(n)]. (4) 由于P(n)通常较小，因此它的对数ln[p(n)]可以通过它的泰勒级数展开$\ln [1-p(n)]= $$-P(n)+O\left[p(n)^{2}\right] $，代入公式(4)可得：
T≈−ln(1−pt)p(n). (5) 1.2.3 采样方法
算法的复杂程度和采样方法有很大关系，下一步将会详述本文的采样方法. 因为形状是一种局部现象，两个点越近，它们属于同一个平面的概率就越大. 利用这一特点，能够大幅度提高采样效率. Myatt(2002)已经证明，可以通过利用形状的局部性来采样，从而增加模型内点的数量. 通常在随机采样的时候，常常使用给定半径的圆来随机挑选样本点，但半径需要预先通过点的密度和分布来确定. 然而，对于不同的模型，离群点的密度和分布变化很大，即使在同一个模型的不同位置，离群点的密度也会急剧变化. 因此，本文采用了一种方法来适应离群点的密度. 八叉树结构是一种可有效用于建立采样点之间空间邻近性的方法. 首先，无约束地选择第一个点P1以创建候选平面，然后随机从八叉树的结构层中挑选一个包含P1的单元C. 最后，在单元C中挑出剩余的K-1个样本点. 使用该方法找到包含n个点的平面Ψ的概率是：
plocal (n)=p(p1∈Ψ)p(p2…pk∈C). (6) 在这个方程式中，第一个概率值是n/N，第二个概率值取决于C集元素的选取. 如果平面Ψ中有大量的点都包含在元素集C中，C将被视为一个优选. 对于一个平面上的大多数点，除了边界点和边缘点之外，它们都有属于这个平面的近邻点. 一般来说，虽然不能通过八叉树结构的元素集来确定它的邻点，但候选平面模型需要足够多的点，才能使它在实际数据中更加完备. 因此，除了少数点，这些近邻点的数量必须和八叉树结构的元素集数量一样大. 为了便于分析，假设元素集C包含平面Ψ中所有的点Pi (Pi$ \subset $ Ψ)，平面Ψ中所有的点的数量是元素集C中点的数量的一半，而且，元素集C中另一半的点是离群点或者噪音点. 选择一个大的元素集C的概率保守估计为1/d，d是八叉树结构的深度. 因此，从集合C中挑选出点P2P3(P2P3$ \subset $Ψ)的条件概率能够通过公式(7)计算出来，将公式(7)代入公式(6)，可得到公式(8).
(|C|/2k−1)(|C|k−1)≈(12)k−1, (7) Plocal (n)=nNd2k−1. (8) 1.2.4 评分方法
评价函数$\sigma_{p} $用来评估已被提取的待选平面. 这个评价函数主要包含以下3个方面：(1)当代选平面被创建后，将到这个平面的距离小于距离阈值ε的点视为待选平面内的点；(2)对满足距离要求的点进行进一步的过滤，当被测点的法向量和待选平面的法向量之间的夹角小于角度阈值α时，将这些点选为这个平面内的点；(3)此外，在所提的方法中加入了新的连续性阈值β，β代表了点与点之间的连续性，如果数据是不规则采样的，则β应选择最小采样分辨率. 对于已经满足以上两个要求的点，只有满足连续性要求的点才能被选为平面的内点.
简而言之，对于一个平面Ψ，其评价函数可计算如下：
σp(Ψ)=|pΨ|. (9) 例如，平面模型Ψ中的点$p_{\mathit{Ψ}} $能够通过以下两步来定义：
pΨ={p∣p∈p∩d(Ψ,p)<ε⋂arccos(|n(p)⋅n(Ψ,p)|<α}, (10) pΨ=max (11) d(Ψ，P)为点P到平面Ψ的欧几里德距离，n(P)为点P的法向量，n(Ψ，P)为平面模型Ψ的法向量和点P的法向量在平面Ψ上的投影之间的关系，max[component(Ψ，PΨ)]指的是PΨ在平面Ψ上的投影点能构成最大相连部分的点集.
1.3 基于改进的Graham Scan算法的结构面边界精细描绘
假设结构面是非常不规则的平面，本文提出了一种新方法来精确地划分结构面边界. 由于结构面上特征点通常分布在提取的结构面垂直方向的两侧因此，这个三维问题可以通过将点投影到拟合平面转化为二维问题.
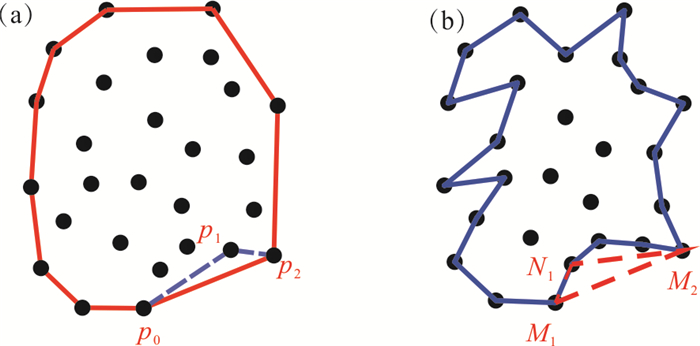
Graham Scan算法是一种非常简单高效的凸多边形算法(Héctor et al., 2020). 总体思路是去掉不属于凸面的点. 给出点云集S，用最小的y坐标在S中求得点P0，按逆时针方向对点进行排序. 从P0开始扫描，如果P0，P1，P2位于凸面上，它们必须满足以下性质：P2位于向量 < P1，P2 > 的左边，否则，应移除P1.
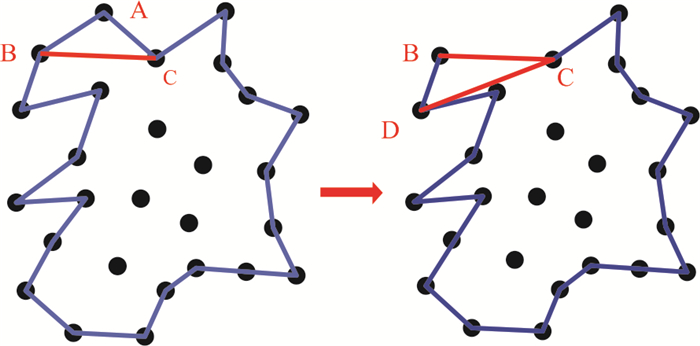
但这种算法获得的边界是凸形的，而结构面的边界往往兼具凸凹性，因此，为了更精准地描绘出结构面边界，需要对Graham Scan算法进行改进. 对于边界点Mk和非边界点Nj，假设有两条新的线M1⁃N1和N1⁃M2，如果由两条新线和M1⁃M2组成的三角形不包含新的边界点，由M1⁃N1和N1⁃M2构成的角度满足凹角的公差要求，N1将会被视为一个新的边界点. 此外，对于两条新的边，可以用递归算法算出新的边界点. 图 3a和图 3b分别显示了Graham Scan算法和改进的Graham Scan算法的结果.
图 3 (a) Graham Scan边界检测效果；(b)改进后的Graham Scan边界检测效果Fig. 3. (a) Boundary detection using Graham Scan, and (b) Boundary detection using modified Graham Scan最终，基于改进的边界检测算法可以得到包含凹凸特征的边界点. 图 4显示了一组点的提取结果，图 4a显示了拟合平面的结果，图 4b显示了使用改进的Graham Scan算法得到的拟合平面边界描绘.
图 4 (a) 拟合平面的结果；(b)拟合平面的边界描绘Fig. 4. (a) Result of the fitting plane, (b) Boundary delineation of the fitting plane1.4 结构面产状和尺寸计算
1.4.1 产状计算
对于一个平面，其结构面能够表示如下：
A x+B y+C z+D=0, (12) 其平面单位法向量为：
\begin{aligned} N &=\left(N_{x}, N_{y}, N_{z}\right) \\ &=(A, B, C) / \sqrt{A^{2}+B^{2}+C^{2}} \end{aligned} , (13) 结构面产状能够利用拟合平面的法向量，通过以下公式计算出：
当$N_{z}>0 $时，
\begin{aligned} &\beta=\cos ^{-1}\left(N_{z}\right) \end{aligned} (14) 此时，若$N_{x} \geqslant 0 $，
\alpha=\cos ^{-1} \frac{N_{y}}{\sqrt{N_{z}{ }^{2}+N_{y}{ }^{2}}} , (15) 若$N_{x}<0 $，
\alpha=2 \pi-\cos ^{-1} \frac{N_{y}}{\sqrt{N_{z}{ }^{2}+N_{y}{ }^{2}}} , (16) 当$N_{z}<0 $时，
\beta=\cos ^{-1}\left(-N_{z}\right) , (17) 此时，若$-N_{x} \geqslant 0 $，
\alpha=\cos ^{-1} \frac{-N_{y}}{\sqrt{N_{z}^{2}+N_{y}^{2}}} , (18) 若$ -N_{x}<0$，
\alpha=2 \pi-\cos ^{-1} \frac{N_{y}}{\sqrt{N_{z}{ }^{2}+N_{y}{ }^{2}}} , (19) 其中：α表示结构面的倾向；β表示结构面倾角.
1.4.2 尺寸计算
结构面的尺寸可以反映结构面的大小，是重要的结构面几何参数. 在上一小节中，表征结构面轮廓的特征点已经被识别出来，基于Graham Scan算法得出的计算结果，可以利用Ear clipping算法进行三角化. 如图 5所示，这里有3个点A，B和C，当A点对应凸角时，线段BC绝对存在于多边形中，然后将A从多边形边界移除，切断三角形ABC. 重复这一过程，直至这个多边形完全被切割成三角形. 最终，结构面的面积就是所有三角形面积的总和.
得到结构面面积S后，用面积大小与其相等的等效圆代替该结构面，用结构面各节点坐标的均值作为该圆的圆心，其半径大小满足以下面积公式：
S=\pi r^{2} , (20) 求得等效圆半径r，以表征结构面的尺寸信息.
2. 实例分析
为了验证所提算法的有效性，分别选取标准几何体点云数据和一处实际边坡点云数据进行分析.
2.1 标准立方体点云数据
创建1 m×1 m×1 m的立方体模型(如图 6a所示)，各平面产状及尺寸可预先计算. 基于模型生成包含100万点的立方体点云模型(如图 6b所示). 假设Y正轴是正北方向，X正轴为正东方向，Z正轴向上，那么立方体的6个面产状可以计算出来，分别为0°∠0°，0°∠180°，90°∠90°，90°∠90°，90°∠180°，90°∠180°. 同理，立方体6个平面的面积均为1 m2，可得等效半径r为0.56 m.
图 6 (a) 立方体模型；(b)立方体点云模型；(c)立方体平面识别Fig. 6. (a)Cube Model; (b) cube point cloud Model; (c) identification of cube plane根据所提方法，可以自动识别出该立方体所包含的6个平面，将法向量一致的平面赋予同样的颜色，以便于可视化分析(如图 6c所示). 平面产状和等效半径计算结果如表 1所示. 结果表明，对于标准立方体数据，所提方法识别的平面产状与理论值完全一致，等效半径存在一部分误差，是因为边界点在识别的时候有所损失，但是最大识别误差率仅为0.357%.
表 1 立方体平面几何信息提取Table Supplementary Table Extraction of geometric properties of cube plane平面 点云数量 倾角(°) 倾向(°) 面积(m2) 等效圆半径(m) 等效半径识别误差率(%) 平面1 8 162 90 180 0.983 0.559 0.179 平面2 8 134 90 90 0.984 0.56 0 平面3 8 109 0 180 0.979 0.558 0.357 平面4 8 120 0 0 0.981 0.559 0.179 平面5 8 101 90 90 0.986 0.56 0 平面6 8 121 90 0 0.982 0.559 0.179 2.2 标准二十面体点云数据
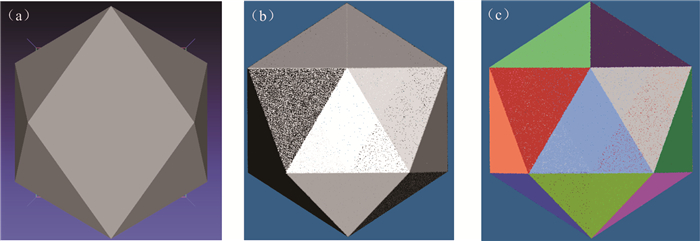
创建边长为2 m的二十面体模型(如图 7a所示)，同样地，各平面产状及尺寸可预先得知. 每个面均为边长为2 m的正三角形，可得该标准20面体每个面的等效圆半径为0.742 m. 基于模型生成包含100万点的立方体点云模型(如图 7b所示). 根据所提方法，可以自动识别出二十面体所包含的二十个平面，将每个平面随机赋予颜色，以便于可视化分析，同时，选取其中6个面进行标注用于定量分析(如图 7c所示). 将自动识别算法计算的这6个平面的产状和等效半径与理论值进行比较，结果如表 2所示. 结果表明，对于二十面体数据，所提方法识别的平面产状识别误差不超过0.91°，等效半径识别的误差百分比不超过1.078%，误差略大于标准立方体，这是由于其形状更为复杂，识别误差随之增大.
图 7 (a) 二十面体模型；(b)二十面体点云模型；(c)二十面体平面识别Fig. 7. (a)Icosahedron Model; (b) Icosahedron point cloud Model; (c) identification of Icosahedron plane表 2 二十面体平面几何信息提取Table Supplementary Table Identification of icosahedron plane平面 点云数量 倾角(°) 倾向(°) 产状差值(°) 面积(m2) 等效圆半径(m) 等效半径识别误差率(%) 平面1 3 595 90 339.1 0.9 1.747 0.746 0.539 平面2 3 498 54.74 315 0.26 1.71 0.738 0.539 平面3 3 626 20.9 360 0.9 1.748 0.746 0.539 平面4 3 463 69.09 90 0.91 1.694 0.734 1.078 平面5 3 538 69.1 270 0.9 1.711 0.738 0.539 平面6 3 599 54.74 225 0.26 1.753 0.747 0.674 2.3 边坡点云数据
为了评估所提方法的有效性，我们选取了边坡的一部分. 这个边坡来自美国科罗拉多州的一个采石场，点云数据存储在数据库中的RockBench(Lato et al., 2013)中. 扫描设备为Optech，采样分辨率在2 cm以下，共扫描4站，约获得151万个点. 图 8a为边坡照片，图 8b为边坡点云模型. 此外，由于大量学者使用相同的数据做过结构面识别(Riquelme et al., 2014)，因此，本文方法得到的结果可以与已发表的数据进行比较. 在本研究中，将结果与Riquelme et al.(2014)的识别结果进行对比分析.
图 8 (a) 边坡照片；(b)边坡点云模型Fig. 8. (a)Picture of the slope, (b) Point cloud data of the slope2.4 结构面智能解译分析
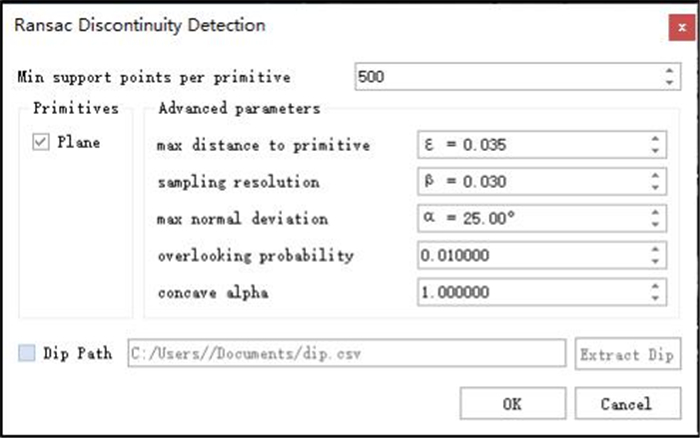
Ransac discontinuity detect (RDD)程序对话框如图 9所示，考虑到真实岩体的结构面是凸凹不平的，因此设定参数如下，其中ε是点到平面的距离，α为点之间的法向量夹角，和β是两点的连续性.
给定边坡的原始点云数据，利用RDD可以智能识别出结构面，不同的颜色代表不同的结构面(如图 10所示). 结果表明，使用RDD不仅可以准确地识别出较为光滑的结构面. 还可以检测出一些破碎的小结构面，甚至包括粗糙度较大的面.
随后，不同的结构面按照其法向量被划分为不同的优势产状组，共计5组. 图 11a为Riquelme论文的结构面分组情况，图 11b为本文所提方法的结构面分组情况. 结果表明，两种方法所提结构面信息保持了较高的一致性，都可以检测出5组结构面，分别为J1、J2、J3、J4和J5. 尽管J1组的平面点数最多，平面最大，但J2、J3、J4和J5仍然可以被检测到.
图 11 结构面分组效果a. Riquelme论文分组效果；b. 所提方法分组效果Fig. 11. Picture showing the discontinuity sets为了更详细地比较这两种方法的识别效果，将对每组结构面进行一一对比. 图 12a~图 12f显示了Riquelme et al.(2014)论文中识别的部分结构面，分别来自J1到J5. 图 13a~图 13f显示了RDD提取的5组代表性结构面. 从图 13可以看出，两种方法提取的J1到J5中的结构面保持了很好的一致性. 用所提出的方法也可以检测出由Riquelme得到的大部分结构面. 需要注意的是，有一些结构面不能被RDD提取，那是因为RDD设置了平面最少点参数NMinPoints对微小结构面进行过滤.
为了定量比较结果，将RDD提取的结构面使用Riquelme的规则进行标记，如图 11所示. 同时，将结构面产状的计算结构汇总在表 3中. 结果表明，如果结构面足够光滑(J1组的大部分结构面)，两种方法之间的误差小于1°，即使对于较为粗糙的结构面(如平面41和平面51)，产状误差率也在6°以内，这是一个合理的误差范围.
表 3 Riquelme和RDD的产状计算结果对比Table Supplementary Table Comparison of discontinuity orientation data between Riquelme and RDD结构面组 Riquelme产状计算结果(°) RDD产状计算结果(°) 差值(°) J1 246.24/39.02(平面11) 244.54/38.60(平面11) 0.42 J1 256.86/52.30(平面12) 77.52/52.94(平面12) 0.64 J1 70.26/35.80(平面13) 250.37/35.83(平面13) 0.03 J1 252.68/35.48(平面14) 251.60/34.00(平面14) 1.48 J1 249.74/35.91(平面15) 250.24/36.12(平面15) 0.11 J1 70.47/35.92(平面16) 70.23/35.72(平面16) 0.24 J1 255.12/32.72(平面17) 251.61/36.00(平面17) 3.51 J2 339.47/83.25(平面21) 334.90/81.72(平面21) 4.57 J2 166.33/76.58(平面22) 346.15/72.81(平面22) 3.77 J2 160.20/89.86(平面23) 338.01/89.08(平面23) 1.22 J2 173.55/76.85(平面24) 353.81/76.58(平面24) 0.27 J3 136.59/82.58(平面31) 135.12/78.43(平面31) 4.15 J3 131.25/82.67(平面32) 317.69/87.73(平面32) 5.06 J3 143.91/89.70(平面33) 327.33/89.84(平面33) 0.14 J4 97.55/63.22(平面41) 99.30/68.12(平面41) 4.90 J4 91.07/50.19(平面42) 92.60/48.67(平面42) 1.53 J4 96.64/47.97(平面43) 96.59/48.04(平面43) 0.07 J5 123.42/76.15(平面51) 125.63/81.94(平面51) 5.79 J5 105.75/69.94(平面52) 106.90/70.43(平面52) 1.15 由于Riquelme et al.(2014)并没有计算结构面的尺寸，因此，所提方法的结构面尺寸计算结果将与经典点云处理软件CAD计算结果进行对比. 表 4列出了两种方法的结构面尺寸计算结果. 结果表明，RDD程序计算的结构面面积CAD的计算面积有较好的一致性，最大误差率不超过0.278%，主要原因是平面22边缘不平整，RDD识别过程损失了一些边缘点.
表 4 CAD和RDD的结构面尺寸计算结果对比Table Supplementary Table Comparison of discontinuity dimension data between Polyworks and RDD结构面组 CAD计算面积(m2) RDD计算面积(m2) CAD计算尺寸(m) RDD计算尺寸(m) 尺寸误差率(%) J1 15.300 0(平面11) 15.321 7(平面11) 2.206 8 2.208 4 0.073 J1 0.435 2(平面12) 0.434 1(平面12) 0.372 2 0.371 7 0.134 J1 2.864 1(平面13) 2.863 6(平面13) 0.954 8 0.954 7 0.010 J1 23.321 2(平面14) 23.339 8(平面14) 2.724 6 2.725 7 0.040 J1 1.176 8(平面15) 1.174 9(平面15) 0.612 0 0.611 5 0.082 J1 5.935 9(平面16) 5.938 9(平面16) 1.374 6 1.374 9 0.022 J1 18.430 0(平面17) 18.429 2(平面17) 2.422 1 2.422 0 0.004 J2 1.355 2(平面21) 1.351 3(平面21) 0.656 8 0.655 8 0.152 J2 0.913 8(平面22) 0.918 9(平面22) 0.539 3 0.540 8 0.278 J2 2.102 0(平面23) 2.107 0(平面23) 0.818 0 0.819 0 0.122 J2 4.199 6(平面24) 4.194 6(平面24) 1.156 2 1.155 5 0.061 J3 15.380 0(平面31) 15.376 0(平面31) 2.212 6 2.212 3 0.014 J3 1.005 9(平面32) 1.002 8(平面32) 0.565 9 0.565 0 0.159 J3 2.134 8(平面33) 2.130 8(平面33) 0.824 3 0.823 6 0.085 J4 1.170 0(平面41) 1.170 0(平面41) 0.610 3 0.610 3 0 J4 6.971 6(平面42) 6.976 5(平面42) 1.489 7 1.490 2 0.034 J4 2.933 3(平面43) 2.930 3(平面43) 0.966 3 0.965 8 0.052 J5 2.955 4(平面51) 2.951 3(平面51) 0.969 9 0.969 2 0.072 J5 8.485 6(平面52) 8.491 1(平面52) 1.643 5 1.644 0 0.030 3. 结论
本文提出了一种基于点云数据的岩体结构面自动提取方法. 该方法主要包括以下步骤：(1)计算点云数据的法向量；(2)基于改进Ransac算法的平面提取；(3)基于改进Graham扫描算法的结构面边界精细化描绘；(4)基于法向量和结构面边界计算结构面产状和尺寸.
本研究提出的方法可以直接基于原始点云数据识别结构面，避免了三角网格化带来的误差和数据损失. 对标准的立方体数据和十二面体数据，RDD计算的产状结果和模型已知的产状最大误差为0.9°，尺寸的最大误差率在1%左右. 与此同时，在实际边坡案例中，将RDD提取的结构面产状与Riquelme方法提取的产状进行比较，产状结果保持了较好的一致性，对于较为光滑的结构面，RDD与Riquelme的误差在1°以内；对于粗糙面，产状误差在6°以内，在工程误差范围内. 将RDD的结构面尺寸计算结果与CAD手动计算结果做对比，显示了高度的一致性，尺寸误差率最大为0.278%，符合工程精度要求.
然而，对于结构面的其他参数，如粗糙度、间距和风化程度等，在本研究中没有提及. 因此，在后续的研究中，将对RDD的功能进行扩充，以实现结构面参数系统性自动识别.
-
图 1 [Qi]是Pi的近邻点集，n是Pi的法向量
Fig. 1. Qi is the subset of Pi, n is the normal vector of Pi
图 3 (a) Graham Scan边界检测效果；(b)改进后的Graham Scan边界检测效果
Fig. 3. (a) Boundary detection using Graham Scan, and (b) Boundary detection using modified Graham Scan
图 4 (a) 拟合平面的结果；(b)拟合平面的边界描绘
Fig. 4. (a) Result of the fitting plane, (b) Boundary delineation of the fitting plane
图 6 (a) 立方体模型；(b)立方体点云模型；(c)立方体平面识别
Fig. 6. (a)Cube Model; (b) cube point cloud Model; (c) identification of cube plane
图 7 (a) 二十面体模型；(b)二十面体点云模型；(c)二十面体平面识别
Fig. 7. (a)Icosahedron Model; (b) Icosahedron point cloud Model; (c) identification of Icosahedron plane
图 8 (a) 边坡照片；(b)边坡点云模型
Fig. 8. (a)Picture of the slope, (b) Point cloud data of the slope
图 11 结构面分组效果
a. Riquelme论文分组效果；b. 所提方法分组效果
Fig. 11. Picture showing the discontinuity sets
Algorithm 1 基于改进的Ransac算法提取平面
Algorithm 1. Extract plane based on modified Ransac algorithm
Input: P is a matrix which stores the point cloud. Output #1：Ψ is a matrix which stores the parameters of the extracted discontinuities.
Output #2：Pψ is a matrix which stores the points belonging to the corresponding discontinuities.
1：Ψ←Φ{extracted discontinuities}
2：C ←Φ{discontinuities candidates}
3: repeat
4: C ← C ∪ new candidates ()
5: m←best candidate(C)
6: if P(|m|, |c|)＞pt then
7: P ← P\Pm {remove points}
8: Ψ←Ψ ∪ m
9: C←C\Cm {remove invalid candidates}
10: end if
11: until P(τ, |c|)＞pt
12: return Ψ
下载: 导出CSV
表 1 立方体平面几何信息提取
Table 1. Extraction of geometric properties of cube plane
平面 点云数量 倾角(°) 倾向(°) 面积(m2) 等效圆半径(m) 等效半径识别误差率(%) 平面1 8 162 90 180 0.983 0.559 0.179 平面2 8 134 90 90 0.984 0.56 0 平面3 8 109 0 180 0.979 0.558 0.357 平面4 8 120 0 0 0.981 0.559 0.179 平面5 8 101 90 90 0.986 0.56 0 平面6 8 121 90 0 0.982 0.559 0.179
下载: 导出CSV
表 2 二十面体平面几何信息提取
Table 2. Identification of icosahedron plane
平面 点云数量 倾角(°) 倾向(°) 产状差值(°) 面积(m2) 等效圆半径(m) 等效半径识别误差率(%) 平面1 3 595 90 339.1 0.9 1.747 0.746 0.539 平面2 3 498 54.74 315 0.26 1.71 0.738 0.539 平面3 3 626 20.9 360 0.9 1.748 0.746 0.539 平面4 3 463 69.09 90 0.91 1.694 0.734 1.078 平面5 3 538 69.1 270 0.9 1.711 0.738 0.539 平面6 3 599 54.74 225 0.26 1.753 0.747 0.674
下载: 导出CSV
表 3 Riquelme和RDD的产状计算结果对比
Table 3. Comparison of discontinuity orientation data between Riquelme and RDD
结构面组 Riquelme产状计算结果(°) RDD产状计算结果(°) 差值(°) J1 246.24/39.02(平面11) 244.54/38.60(平面11) 0.42 J1 256.86/52.30(平面12) 77.52/52.94(平面12) 0.64 J1 70.26/35.80(平面13) 250.37/35.83(平面13) 0.03 J1 252.68/35.48(平面14) 251.60/34.00(平面14) 1.48 J1 249.74/35.91(平面15) 250.24/36.12(平面15) 0.11 J1 70.47/35.92(平面16) 70.23/35.72(平面16) 0.24 J1 255.12/32.72(平面17) 251.61/36.00(平面17) 3.51 J2 339.47/83.25(平面21) 334.90/81.72(平面21) 4.57 J2 166.33/76.58(平面22) 346.15/72.81(平面22) 3.77 J2 160.20/89.86(平面23) 338.01/89.08(平面23) 1.22 J2 173.55/76.85(平面24) 353.81/76.58(平面24) 0.27 J3 136.59/82.58(平面31) 135.12/78.43(平面31) 4.15 J3 131.25/82.67(平面32) 317.69/87.73(平面32) 5.06 J3 143.91/89.70(平面33) 327.33/89.84(平面33) 0.14 J4 97.55/63.22(平面41) 99.30/68.12(平面41) 4.90 J4 91.07/50.19(平面42) 92.60/48.67(平面42) 1.53 J4 96.64/47.97(平面43) 96.59/48.04(平面43) 0.07 J5 123.42/76.15(平面51) 125.63/81.94(平面51) 5.79 J5 105.75/69.94(平面52) 106.90/70.43(平面52) 1.15
下载: 导出CSV
表 4 CAD和RDD的结构面尺寸计算结果对比
Table 4. Comparison of discontinuity dimension data between Polyworks and RDD
结构面组 CAD计算面积(m2) RDD计算面积(m2) CAD计算尺寸(m) RDD计算尺寸(m) 尺寸误差率(%) J1 15.300 0(平面11) 15.321 7(平面11) 2.206 8 2.208 4 0.073 J1 0.435 2(平面12) 0.434 1(平面12) 0.372 2 0.371 7 0.134 J1 2.864 1(平面13) 2.863 6(平面13) 0.954 8 0.954 7 0.010 J1 23.321 2(平面14) 23.339 8(平面14) 2.724 6 2.725 7 0.040 J1 1.176 8(平面15) 1.174 9(平面15) 0.612 0 0.611 5 0.082 J1 5.935 9(平面16) 5.938 9(平面16) 1.374 6 1.374 9 0.022 J1 18.430 0(平面17) 18.429 2(平面17) 2.422 1 2.422 0 0.004 J2 1.355 2(平面21) 1.351 3(平面21) 0.656 8 0.655 8 0.152 J2 0.913 8(平面22) 0.918 9(平面22) 0.539 3 0.540 8 0.278 J2 2.102 0(平面23) 2.107 0(平面23) 0.818 0 0.819 0 0.122 J2 4.199 6(平面24) 4.194 6(平面24) 1.156 2 1.155 5 0.061 J3 15.380 0(平面31) 15.376 0(平面31) 2.212 6 2.212 3 0.014 J3 1.005 9(平面32) 1.002 8(平面32) 0.565 9 0.565 0 0.159 J3 2.134 8(平面33) 2.130 8(平面33) 0.824 3 0.823 6 0.085 J4 1.170 0(平面41) 1.170 0(平面41) 0.610 3 0.610 3 0 J4 6.971 6(平面42) 6.976 5(平面42) 1.489 7 1.490 2 0.034 J4 2.933 3(平面43) 2.930 3(平面43) 0.966 3 0.965 8 0.052 J5 2.955 4(平面51) 2.951 3(平面51) 0.969 9 0.969 2 0.072 J5 8.485 6(平面52) 8.491 1(平面52) 1.643 5 1.644 0 0.030
下载: 导出CSV
-
Chen, J.Q., Zhu, H.H., Li, X.J., 2016. Automatic Extraction of Discontinuity Orientation from Rock Mass Surface 3D Point Cloud. Computers and Geosciences, 95: 18-31. https://doi.org/10.1016/j.cageo.2016.06.015. Chen, Z.F., Chen, D.L., Yang, J.X., 2012. Application of Three⁃Dimensional Laser Scanning Technique in Deformation Monitoring of Excavations. Chinese Journal of Geotechnical Engineering, 34(Suppl): 557-559 (in Chinese with English abstract). http://www.en.cnki.com.cn/Article_en/CJFDTotal-BJCH2017S1040.htm Deb, D., Hariharan, S., Rao, U.M., et al. , 2007. Automatic Detection and Analysis of Discontinuity Geometry of Rock Mass from Digital Images. Computers and Geosciences, 34(2): 115-126. https://doi.org/10.1016/j.cageo.2007.03.007. Dong, X.J., Huang, R.Q., 2006. Application of 3D Laser Scanning Technology to Geologic Survey of High and Steep Slope. Chinese Journal of Rock Mechanics and Engineering, 25(S2): 3629-3635 (in Chinese with English abstract). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb2006z2046 Fan, L.M., Li, N., 2005. Study on Rock Mass Joint Measurement Based on Digital Photogrammetry. Chinese Journal of Rock Mechanics and Engineering, 24(5): 792-797 (in Chinese with English abstract). http://www.oalib.com/paper/1485913 Ge, Y.F., Tang, H.M., Xia, D., et al. , 2018. Automated Measurements of Discontinuity Geometric Properties from a 3D⁃Point Cloud Based on a Modified Region Growing Algorithm. Engineering Geology, 242(14): 44-54. https://doi.org/10.1016/j.enggeo.2018.05.007. Gigli, G., Casagli, N., 2010. Semi⁃Automatic Extraction of Rock Mass Structural Data from High Resolution LIDAR Point Clouds. International Journal of Rock Mechanics and Mining Sciences, 48(2): 187-198. https://doi.org/10.1016/j.ijrmms.2010.11.009. Gu, D.Z., 1979. Foundation of Rock Engineering Geomechanics. Science Press, Beijing, 290-329 (in Chinese with English abstract). Héctor, F., Cristóbal, A. N., Hitschfeld, N., 2020. A Filtering Technique for Fast Convex Hull Construction in R2. Journal of Computational and Applied Mathematics, 364: 112-298. https://doi.org/10.1016/j.cam.2019.06.014 Huang, D., Zhong, Z., 2015. A Universal Mathematical Method for Determining Occurrence of Underground Rock Discontinuity Based on TV Picture of Wall of a Single Borehole. Earth Science, 40(6): 1101-1106 (in Chinese with English abstract). http://www.researchgate.net/publication/283749157_A_universal_mathematical_method_for_determining_occurrence_of_underground_rock_discontinuity_based_on_tv_picture_of_wall_of_a_single_borehole Kang, J.T., Wu, Q., Tang, H.M., et al., 2019. Strength Degradation Mechanism of Soft and Hard Interbedded Rock Masses of Badong Formation Caused by Rock/Discontinuity Degradation. Earth Science, 44(11): 3950-3960(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-DQKX201911029.htm Lato, M., Kemeny, J., Harrap, R, M., et al., 2013. Rock Bench: Establishing a Common Repository and Standards for Assessing Rockmass Characteristics Using Lidar and Photogrammetry. Computers and Geosciences, 50: 106-114. https://doi.org/10.1016/j.cageo.2012.06.014. Lato, M.J., VÖge, M., 2012. Automated Mapping of Rock Discontinuities in 3D Lidar and Photogrammetry Models. International Journal of Rock Mechanics and Mining Sciences, 54: 150-158. doi: 10.1016/j.ijrmms.2012.06.003 Li, H. B., Li, X. W., Li, W. Z., et al., 2019. Quantitative Assessment for the Rockfall Hazard in a Post⁃Earthquake High Rock Slope Using Terrestrial Laser Scanning. Engineering Geology, 248: 1-13. https://doi.org/10.1016/j.enggeo.2018.11.003. Lin, S., Wang, W., Deng, X.H., et al., 2019. Geophysical Observation of Typical Landslides in Three Gorges Reservoir Area and Its Significance: A Case Study of Sifangbei Landslide in Wanzhou District. Earth Science, 44(9): 3135-3146(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-DQKX201909026.htm Myatt, D. R., Torr, P. H. S., Nasuto, S. J., et al., 2002. NAPSAC: High Noise, High Dimensional Model Parameterization: It's in the Bag. British Machine Vision Conference. DBLP., 458-467. http://www.researchgate.net/publication/221259336_NAPSAC_High_Noise_High_Dimensional_Robust_Estimation_-_it's_in_the_Bag Math, J., Samson, C., McKinnon, S.D., 2011. 3D Laser Imaging for Joint Orientation Analysis. International Journal of Rock Mechanics and Mining Sciences, 48(6): 932-941. https://doi.org/10.1016/j.ijrmms.2011.04.010. Olariu, M.I., Ferguson, J.F., Aiken, C.L.V., et al., 2008. Outcrop Fracture Characterization Using Terrestrial Laser Scanners: Deep⁃Water Jackfork Sandstone at Big Rock Quarry, Arkansas Geosphere, 4(1): 247-259. https://doi.org/10.1130/GES00139.1CorpusID:129157012. Qiu, J.L., Xia, Q.L., Yao, L.Q., et al., 2012. Mine Geological Modeling and Application Based on the Three⁃Dimensional Laser Scanner Technology. Earth Science, 37(6): 1209-1216 (in Chinese with English abstract). http://www.researchgate.net/publication/289046802_Mine_geological_modeling_and_application_based_on_the_three-dimensional_laser_scanner_technology Riquelme, A.J., Riquelme, A., Abellán, R., et al., 2014. A New Approach for Semi⁃Automatic Rock Mass Joints Recognition from 3D Point Clouds. Computers and Geosciences, 68: 38-52. https://doi.org/10.1016/j.cageo.2014.03.014. Slob, S., Hack, H.R.G.K., Feng, Q., et al., 2007. Fracture Mapping Using 3D Laser Scanning Techniques. In: Ribeiro, E., Sousa, L., Olalla, C., eds., Proceeding of the 11th Congress of the International Society for Rock Mechanics, Lisbon, 1: 299-302. Slob, S., Van, K.B., Hack, R., et al., 2005. Method for Automated Discontinuity Analysis of Rock Slopes with Three⁃Dimensional Laser Scanning. Transportation Research Record: Journal of the Transportation Research Board, 1913(1): 187-194. https://doi.org/10.1177/0361198105191300118 Sun, G.Z., 1993. On the Theory of Structure⁃Controlled Rockmass. Journal of Engineering Geology, (1): 14-18 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GCDZ199301003.htm Tang, H.M., Ge, Y.F., Wang, L.Q., et al., 2012. Study on Estimation Method of Rock Mass Discontinuity Shear Strength Based on Three⁃Dimensional Laser Scanning and Image Technique. Journal of Earth Science, 23(6): 908-913. doi: 10.1007/s12583-012-0301-2 Uherčík, M., Kybic, J., Liebgott, H., et al., 2010. Model Fitting Using RANSAC for Surgical Tool Localization in 3D Ultrasound Images. IEEE Transactions on Bio⁃Medical Engineering, 57(8): 1907-16. https://doi.org/10.1109/TBME.2010.2046416 Vöge, M., Lato, M.J., Diederichs, M.S., 2013. Automated Rockmass Discontinuity Mapping from 3⁃Dimensional Surface Data. Engineering Geology, 164: 155-162. https://doi.org/10.1016/j.enggeo.2013.07.008. Wang, J.C., Wang, C.Y., Hu, S., et al., 2017. A New Method for Extraction of Parameters of Structural Surface in Borehole Images. Rock and Soil Mechanics, 38(10): 3074-3080 (in Chinese with English abstract). http://www.researchgate.net/publication/322114200_A_new_method_for_extraction_of_parameters_of_structural_surface_in_borehole_images Wang, M.C., Xu, Z.S., Wang, F.Y., et al., 2018. Fitting Test on Probability Distribution of Discontinuity Parameters in Rock Mass Based on Photogrammetry. Journal of Jilin University (Earth Science Edition), 48(6): 1898-1906 (in Chinese with English abstract). http://www.researchgate.net/publication/330884895_Fitting_Test_on_Probability_Distribution_of_Discontinuity_Parameters_in_Rock_Mass_Based_on_Photogrammetry Warburton, J., Holden, J., Mills, A.J., 2004. Hydrological Controls of Surficial Mass Movements in Peat. Earth Science Reviews, 67(1): 139-156. https://doi.org/10.1016/j.enggeo.2013.07.008. Yuan, G.X., Wang, H.J., Huang, Z.Q., et al., 2017. Distribution of Discontinuities along Drillholes in Granite: Case Study from Dayawan, Shenzhen. Journal of Engineering Geology, 25(4): 1010-1016 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-GCDZ201704015.htm Yu, T.L., 2009. Digital Identification of the Discontinuities Information and Strength Evaluation of the Rockmass (Dissertation). Northeastern University, Shenyang (in Chinese with English abstract). Zhang, P., Du, K., Tannant, D.D., et al., 2018. Automated Method for Extracting and Analyzing the Rock Discontinuities from Point Clouds Based on Digital Surface Model of Rock Mass. Engineering Geology, 239: 109-118. https://doi.org/10.1016/j.enggeo.2018.03.020. 陈致富, 陈德立, 杨建学, 2012. 三维激光扫描技术在基坑变形监测中的应用. 岩土工程学报, 34(S1): 557-559. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2012S1109.htm 董秀军, 黄润秋, 2006. 三维激光扫描技术在高陡边坡地质调查中的应用. 岩石力学与工程学报, 25(2): 3629-3635. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2045.htm 范留明, 李宁, 2005. 基于数码摄影技术的岩体裂隙测量方法初探. 岩石力学与工程学报, 24(5): 792-797. doi: 10.3321/j.issn:1000-6915.2005.05.010 谷德振, 1979. 岩体工程地质力学基础. 北京: 科学出版社, 290-329. 黄达, 钟助, 2015. 基于单个钻孔孔壁电视图像确定地下岩体结构面产状的普适数学方法. 地球科学, 40(6): 1101-1106. doi: 10.3799/dqkx.2015.092 亢金涛, 吴琼, 唐辉明, 等, 2019. 岩石/结构面劣化导致巴东组软硬互层岩体强度劣化的作用机制. 地球科学, 44(11): 3950-3960. doi: 10.3799/dqkx.2019.110 林松, 王薇, 邓小虎, 等, 2019. 三峡库区典型滑坡地球物理实测及其意义: 以万州区四方碑滑坡为例. 地球科学, 44(9): 3135-3146. doi: 10.3799/dqkx.2019.074 邱俊玲, 夏庆霖, 姚凌青, 等, 2012. 基于三维激光扫描技术的矿山地质建模与应用. 地球科学, 37(6): 1209-1216. http://www.earth-science.net/article/id/2326 孙广忠, 1993. 论"岩体结构控制论". 工程地质学报, 1(1): 14-18. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ199301003.htm 汪进超, 王川婴, 胡胜, 等, 2017. 孔壁钻孔图像的结构面参数提取方法研究. 岩土力学, 38(10): 3074-3080. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201710040.htm 王明常, 徐则双, 王凤艳, 等, 2018. 基于摄影测量获取岩体结构面参数的概率分布拟合检验. 吉林大学学报(地球科学版), 48(6): 1898-1906. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201806027.htm 袁广祥, 王洪建, 黄志全, 等, 2017. 花岗岩体钻孔中结构面的分布规律——以深圳大亚湾花岗岩体为例. 工程地质学报, 25(4): 1010-1016. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201704015.htm 于天亮, 2009. 岩体结构面信息数字识别及强度评价(硕士学位论文). 沈阳: 东北大学. 期刊类型引用(13)
1. 徐志华，郭戈，孙钱程，丰光亮，何钰铭，谢迪. 改进的区域生长算法在三维激光点云识别岩体结构面中的应用. 水文地质工程地质. 2024(02): 101-112 . 
百度学术2. 李志刚，叶宏林，代云云，徐光黎，盛逸凡，马郧. 干湿循环作用下云母石英片岩抗剪性能劣化规律及机理. 地球科学. 2024(03): 1028-1038 . 
本站查看3. 张茹，吕游，张泽天，任利，谢晶，张安林，严志伟，米欧. 深地工程多维信息感知与智能建造的发展与展望. 煤炭学报. 2024(03): 1259-1290 . 百度学术4. 杨成龙，缑慧娟. 基于无人机倾斜摄影技术和三维点云技术的碎裂松动岩体结构面识别研究. 水利与建筑工程学报. 2024(05): 24-29 . 百度学术5. 尹文旭，黄健，张冰冰，周琨. 考虑体积与形状不确定性的高位危岩风险量化评估研究. 工程地质学报. 2024(05): 1683-1695 . 百度学术6. 车德福，钟壬清，马保东，蒋紫薇. 改进RANSAC的无人机三维模型建筑轮廓半自动提取. 桂林理工大学学报. 2024(04): 649-655 . 百度学术7. 李翠，李杰林，张良兵，杨承业，徐继业，周科平. 基于无人机贴近测量的露天矿岩质边坡结构面自动识别. 金属矿山. 2023(02): 146-153 . 百度学术8. 陈昌富，何旷宇，余加勇，毛凤山，薛现凯，李锋. 基于无人机贴近摄影的高陡边坡结构面识别. 湖南大学学报(自然科学版). 2022(01): 145-154 . 百度学术9. 王述红，魏崴，陈浩，尹宏. 基于HDBSCAN算法的岩体结构面产状识别及分组方法. 东北大学学报(自然科学版). 2022(06): 888-896 . 百度学术10. 李胜，熊自明，刘一鸣，李志浩. 基于改进DBSCAN算法的岩体结构面智能识别方法. 隧道与地下工程灾害防治. 2022(02): 49-58 . 百度学术11. 董文川，张文，李腾跃，陈俊淇，王佳，李万堃，尹韩，赵潇涵，蓝升，潘晓娟. 高陡岩质斜坡坡表实景模型构建与岩体结构面自动解译方法及平台研发. 地球科学与环境学报. 2022(06): 1066-1082 . 百度学术12. 罗泽军，张清照，石振明，潘青，俞松波. 考虑表面形貌特征的岩体结构面蠕变特性. 地球科学. 2022(12): 4484-4497 . 本站查看13. 柴波，史绪山，杜娟，王伟，钱未. 如何实现区域岩体结构精细化分析？综述与设想. 地球科学. 2022(12): 4629-4646 . 本站查看其他类型引用(12)
-
下载:
百度学术
点击查看大图
计量
- 文章访问数: 3008
- HTML全文浏览量: 1398
- PDF下载量: 199
- 被引次数: 25
