Effect of Coefficient of Variation of Particle Size of Porous Media on Contaminant Transport
-
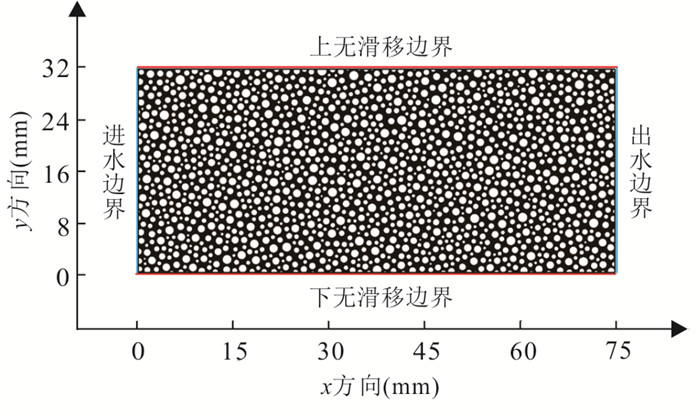
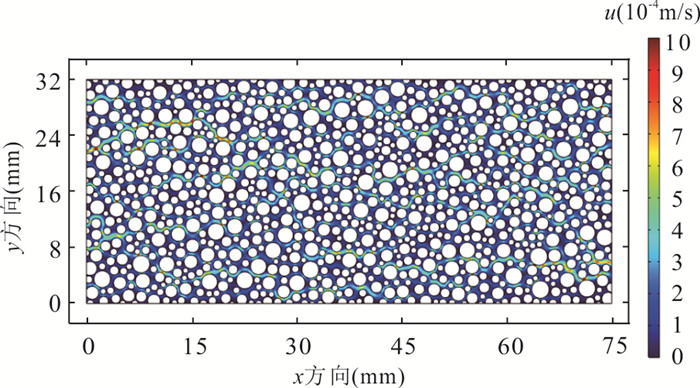
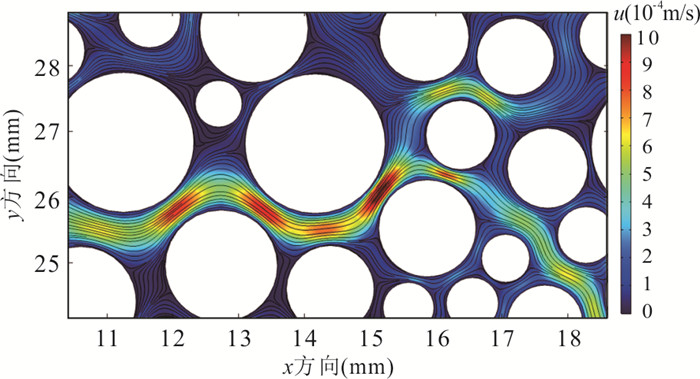
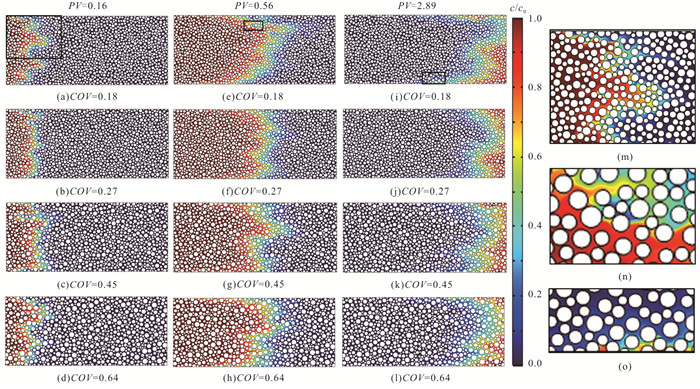
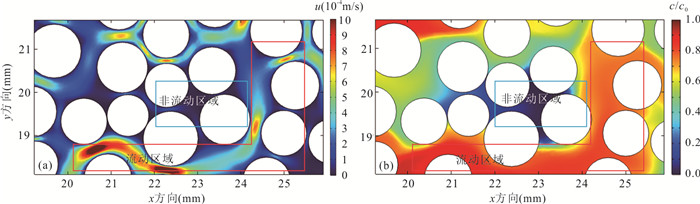
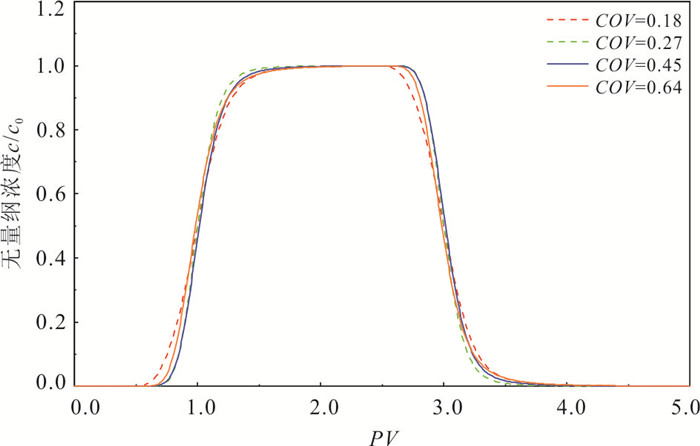
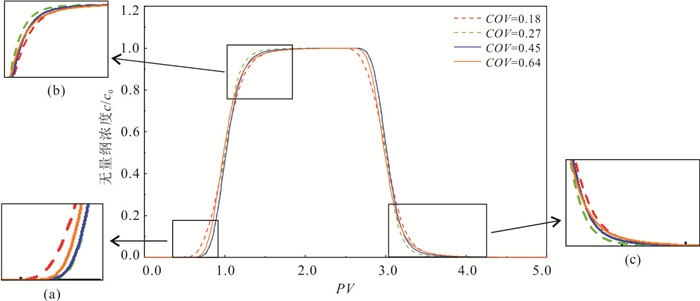
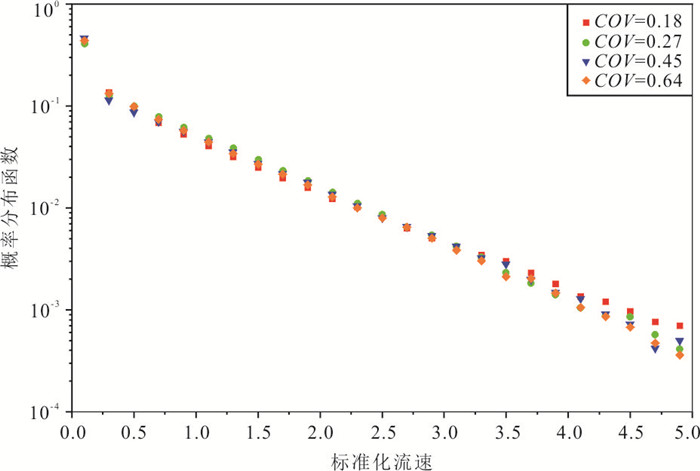
摘要: 多孔介质污染物运移对于明晰地下水污染很重要，但在多孔介质中粒径变异系数（coefficient of variation，COV）对内部微观孔隙结构中污染物运移过程影响的研究还存在不足.为此，基于随机算法，提出了一种不同COV且孔隙度一致的多孔介质几何模型构建方法，通过对Navier-Stokes（N-S）方程和对流‒扩散方程（advection-diffusion equation，简称ADE）进行耦合求解得到多孔介质地下水流场及污染物浓度场，引入克里斯琴森均匀系数，定量评价流场流速分布的均匀性，基于MIM（mobile and immobile）模型和ADE模型分析耦合求解得到的穿透曲线特征.结果表明：随着粒径COV的增大，流场流速分布的不均性增强，MIM模型中的溶质流动区域占比$ \beta $、无量纲传质率$ {\alpha }^{*} $均增大；MIM模型拟合优度高于ADE模型，且随COV增大，ADE模型的拟合全局误差$ {E}_{\mathrm{i}} $逐步增大.总体上，粒径COV控制了溶质流动区域和非流动区域的大小及其之间的溶质交换强度，造成了多孔介质内部溶质运移的“非费克”行为，使得ADE模型的误差逐步增大，对于较大COV的多孔介质，MIM模型具有更好的适用性.Abstract: The contaminant transport in porous media is crucial for a comprehensive understanding of groundwater contamination. However, there are still inadequacies in the research concerning the effect of the coefficient of variation (COV) of particle size of porous media on the contaminant transport in the internal microscopic pore structure. A method is proposed to construct a geometric model of porous media with different coefficients of variation and consistent porosity based on a random algorithm. The groundwater flow field and contaminant concentration field in porous media are obtained by coupling the Navier-Stokes equation and the advection-diffusion equation. The uniformity of flow velocity distribution is evaluated quantitatively by introducing Christiansen uniformity coefficient. Based on the MIM (mobile and immobile) model and the ADE (advection-dispersion equation) model, the characteristics of breakthrough curves are analyzed. The results show that as the COV of particle size increases, the non-uniformity of the flow velocity distribution is enhanced. The COV of particle size is positively correlated with the ratio of solute mobile domain $ \beta $ and the dimensionless mass transfer rate $ {\alpha }^{*} $; the goodness-of-fitting of MIM model is better than that of ADE model, and as the COV increases, the fitting global error $ {E}_{\mathrm{i}} $ of ADE model gradually increases. Overall, the COV of particle size controls the size of mobile and immobile domain and solute exchange intensity between two domains, resulting in the non-Fickian behavior of solute transport in porous media. This also causes the error of ADE model gradually increases. MIM model has better applicability for the porous media with larger COV.
-
Key words:
- porous media /
- contaminant transport /
- coefficient of variation /
- breakthrough curve /
- inverse model /
- groundwater
-
图 4 孔隙结构内部优先流现象（COV=0.64）
Fig. 4. Preferential flow phenomenon in pore structure(COV=0.64)
图 6 (a) 水流场及(b)浓度场中流动区域与非流动区域分布
Fig. 6. Mobile and immobile domain distribution in (a) flow field and (b) concentration field
图 7 不同COV的多孔介质内部污染物运移穿透曲线
Fig. 7. Contaminant transport breakthrough curves in porous media with different coefficients of variation
图 9 标准化流速概率分布函数曲线
Fig. 9. Probability distribution functions of the normalized flow velocity
图 10 不同COV的MIM模型及ADE模型拟合穿透曲线
Fig. 10. Fitted breakthrough curves with different coefficients of variation based on MIM model and ADE model
表 1 不同COV多孔介质流速均匀性评价指标
Table 1. Evaluation indices of flow velocity uniformity of the porous media with different coefficients of variation
COV CV $ {\gamma }_{\mathrm{\upsilon }} $ CU 0.18 1.253 4 0.546 4 0.092 8 0.27 1.108 1 0.580 4 0.160 8 0.45 1.231 8 0.537 4 0.074 9 0.64 1.161 5 0.564 3 0.128 5 
下载: 导出CSV
表 2 不同COV多孔介质的MIM模型和ADE模型拟合优度统计结果
Table 2. Statistical results from the goodness-of-fitting of the MIM model and ADE model for porous media with different coefficients of variation
COV MIM模型 ADE模型 $ {{R}^{2}}_{\mathrm{M}\mathrm{I}\mathrm{M}} $ $ {E}_{\mathrm{M}\mathrm{I}\mathrm{M}} $ $ {{R}^{2}}_{\mathrm{A}\mathrm{D}\mathrm{E}} $ $ {E}_{\mathrm{A}\mathrm{D}\mathrm{E}} $ 0.18 0.999 9 0.005 925 0.999 8 0.005 458 0.27 1.000 0 0.001 071 0.999 9 0.004 751 0.45 1.000 0 0.001 614 0.999 8 0.006 208 0.64 1.000 0 0.000 863 0.999 6 0.009 094
下载: 导出CSV
表 3 不同COV多孔介质的MIM模型和ADE模型参数估计值
Table 3. Estimated values of parameters from the MIM model and ADE model for porous media with different coefficients of variation
COV MIM模型 ADE模型 $ \beta $ $ {\alpha }^{*} $a $ {D}_{\mathrm{L},\mathrm{M}\mathrm{I}\mathrm{M}} $
(m2·s‒1)$ {\lambda }_{\mathrm{M}\mathrm{I}\mathrm{M}} $b(m) $ {\stackrel{-}{u}}_{\mathrm{f}\mathrm{i}\mathrm{t},\mathrm{M}\mathrm{I}\mathrm{M}}/\stackrel{-}{u} $ $ {D}_{\mathrm{L},\mathrm{A}\mathrm{D}\mathrm{E}} $
(m2·s-1)$ {\lambda }_{\mathrm{A}\mathrm{D}\mathrm{E}} $c
(m)$ {\stackrel{-}{u}}_{\mathrm{f}\mathrm{i}\mathrm{t},\mathrm{A}\mathrm{D}\mathrm{E}}/\stackrel{-}{u} $ 0.18 0.71 0.003 0.134 843.032 0.54 0.193 1214.218 0.77 0.27 0.98 0.128 0.076 478.138 0.80 0.089 559.925 0.80 0.45 0.98 0.132 0.091 572.507 0.81 0.111 698.333 0.82 0.64 0.96 0.201 0.104 654.294 0.79 0.140 880.780 0.80 注：$ {\alpha }^{*} $a表示无量纲传质率；$ {\lambda }_{\mathrm{M}\mathrm{I}\mathrm{M}} $b表示MIM模型的拟合弥散度，$ {\lambda }_{\mathrm{M}\mathrm{I}\mathrm{M}}={D}_{\mathrm{L},\mathrm{M}\mathrm{I}\mathrm{M}}/\stackrel{-}{u} $；$ {\lambda }_{\mathrm{A}\mathrm{D}\mathrm{E}} $c表示ADE模型的拟合弥散度，$ {\lambda }_{\mathrm{A}\mathrm{D}\mathrm{E}}={D}_{\mathrm{L},\mathrm{A}\mathrm{D}\mathrm{E}}/\stackrel{-}{u} $.
下载: 导出CSV
-
Bijeljic, B., Raeini, A., Mostaghimi, P., et al., 2013. Predictions of Non⁃Fickian Solute Transport in Different Classes of Porous Media Using Direct Simulation on Pore–Scale Images. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 87(1): 013011. https://doi.org/10.1103/PhysRevE.87.013011 Cheng, Z., Xu, H. X., Sun, Y. Y., et al., 2017. Effect of Salinity on DNAPL Migration and Distribution in Saturated Porous Media. Hydrogeology & Engineering Geology, 44(4): 129-136 (in Chinese with English abstract). Dou, Z., Sleep, B., Zhan, H. B., et al., 2019a. Multiscale Roughness Influence on Conservative Solute Transport in Self–Affine Fractures. International Journal of Heat and Mass Transfer, 133: 606-618. https://doi.org/10.1016/j.ijheatmasstransfer.2018.12.141 Dou, Z., Zhang, X. Y., Chen, Z., et al., 2019b. Effects of Cemented Porous Media on Temporal Mixing Behavior of Conservative Solute Transport. Water, 11(6): 1204. https://doi.org/10.3390/w11061204 Gao, G. Y., Zhan, H. B., Feng, S. Y., et al., 2010. A New Mobile–Immobile Model for Reactive Solute Transport with Scale–Dependent Dispersion. Water Resources Research, 46(8): W08533. https://doi.org/10.1029/2009WR008707 Goltz, M. N., Roberts, P. V., 1986. Three⁃Dimensional Solutions for Solute Transport in an Infinite Medium with Mobile and Immobile Zones. Water Resources Research, 22(7): 1139-1148. https://doi.org/10.1029/WR022i007p01139 Harvey, C., Gorelick, S. M., 2000. Rate–Limited Mass Transfer or Macrodispersion: Which Dominates Plume Evolution at the Macrodispersion Experiment (MADE) Site? Water Resources Research, 36(3): 637-650. https://doi.org/10.1029/1999WR900247 Icardi, M., Boccardo, G., Marchisio, D. L., et al., 2014. Pore–Scale Simulation of Fluid Flow and Solute Dispersion in Three⁃Dimensional Porous Media. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 90(1): 013032. https://doi.org/10.1103/PhysRevE.90.013032 Jiang, L. Q., Sun, R. L., Liang, X., 2021. Predicting Groundwater Flow and Transport in Heterogeneous Aquifer Sandbox Using Different Parameter Estimation Methods. Earth Science, 46(11): 4150-4160 (in Chinese with English abstract). Li, H. W., Bai, B., Wang, M. S., et al., 2015. Contaminant Transport under Seeping Condition in Porous Media with a Contaminant Source of Cyclically Variable Concentration. Rock and Soil Mechanics, 36(5): 1306-1312 (in Chinese with English abstract). Li, T., Jin, S. P., Huang, S. Y., et al., 2013. Evaluation Indices of Flow Velocity Distribution Uniformity: Comparison and Application. Thermal Power Generation, 42(11): 60-63, 92 (in Chinese with English abstract). Li, X., Su, S. L., Wen, Z., Xu, G. Q., 2022. Numerical Analysis of Estimating Groundwater Velocity through Single⁃Well Push⁃Pull Test. Earth Science, 47(2): 633-641 (in Chinese with English abstract). Li, Y. M., Wen, Z., 2020. Impacts of Non⁃Darcian Flow in the Fracture on Flow Field and Solute Plumes in a Fracture⁃Aquifer System. Earth Science, 45(2): 693-700 (in Chinese with English abstract). van Genuchten, M. T., Wierenga, P. J., 1976. Mass Transfer Studies in Sorbing Porous Media I. Analytical Solutions. Soil Science Society of America Journal, 40(4): 473-480. https://doi.org/10.2136/sssaj1976.03615995004000040011x Ye, Y., Zhang, Y., Cai, F. M., et al., 2021. Fluid Deformation and Solute Transport in Macroscopic Anisotropic Porous Media. Advances in Water Science, 32(6): 903-910 (in Chinese with English abstract). Yu, Q. C., Zhu, X. B., Wu, J. C., et al., 2017. Experimental Research of Impact of the Immobile Domain on the Solute Transport. Hydrogeology & Engineering Geology, 44(4): 160-164, 172 (in Chinese with English abstract). Zhang, X. Y., Dou, Z., 2018. Influence of Microscopic Pore Structure of Clay on Soluble Contaminant Transport. Hydrogeology & Engineering Geology, 45(4): 157-164 (in Chinese with English abstract). 程洲, 徐红霞, 孙媛媛, 等, 2017. 盐度对多孔介质中DNAPL运移和分布的影响. 水文地质工程地质, 44(4): 129-136. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201704020.htm 蒋立群, 孙蓉琳, 梁杏, 2021. 含水层非均质性不同刻画方法对地下水流和溶质运移预测的影响. 地球科学, 46(11): 4150-4160. doi: 10.3799/dqkx.2020.268 李华伟, 白冰, 王梦恕, 等, 2015. 渗透作用下多孔介质中循环浓度污染物的迁移过程研究. 岩土力学, 36(5): 1306-1312. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201505010.htm 李坦, 靳世平, 黄素逸, 等, 2013. 流场速度分布均匀性评价指标比较与应用研究. 热力发电, 42(11): 60-63, 92. https://www.cnki.com.cn/Article/CJFDTOTAL-RLFD201311013.htm 李旭, 苏世林, 文章, 许光泉, 2022. 单井注抽试验测算地下水流速的数值分析. 地球科学, 47(2): 633-641. doi: 10.3799/dqkx.2021.102 李一鸣, 文章, 2020. 非达西裂隙流对渗透性基岩中流场及溶质羽的影响. 地球科学, 45(2): 693-700. doi: 10.3799/dqkx.2018.345 叶逾, 张宇, 蔡芳敏, 等, 2021. 宏观各向异性多孔介质中流体变形及溶质运移. 水科学进展, 32(6): 903-910. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ202106009.htm 余期冲, 祝晓彬, 吴吉春, 等, 2017. 死端孔隙对溶质运移影响的实验研究. 水文地质工程地质, 44(4): 160-164, 172. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201704024.htm 张学羿, 窦智, 2018. 黏土微观孔隙结构对可溶性污染物运移的影响. 水文地质工程地质, 45(4): 157-164. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201804023.htm -
点击查看大图
图(10) / 表(3)
计量
- 文章访问数: 815
- HTML全文浏览量: 656
- PDF下载量: 47
- 被引次数: 0
