Complexities of Landslide Moving Path: A Review and Perspective
-
摘要:
滑坡运动路径具有普遍的复杂性,体现为侧散、转向、分叉、交织、聚合与并联等复杂行为.滑坡运动路径复杂性增大了滑坡危险性.因而,滑坡危险性评估对滑坡运动路径复杂度的量化和概率分布研究提出了需求.系统地梳理和总结了滑坡运动路径复杂度的研究现状,指出了相关研究所面临的关键问题,并进行了未来研究展望.总体上,当前关于滑坡运动路径复杂行为的研究,主要面临量化研究稀缺、概率分布研究欠缺的问题.具体表现在:现有滑坡运动路径的剖面线概化方法难以处理多路径复杂行为;现有零星的指标不能满足滑坡运动路径复杂度的系统性科学量化;滑坡运动路径复杂度概率分布的分布函数不明、主控因素不清.进一步,针对待解决的关键问题,本文在研究展望中提出:主要通过分段单路径化方案,实现滑坡运动多路径复杂行为的剖面线概化;构建基于剖面线的滑坡运动路径复杂度的量化指标体系,突破量化难题;基于大量滑坡实例数据,确定滑坡运动路径复杂度概率分布的分布函数、查清其主控因素;最终,实现滑坡运动路径复杂度概率分布的预测建模,支撑滑坡危险性及风险定量评估.
Abstract:Landslide is generally characterized by complex moving paths, reflected by behaviors including spreading, turning, splitting, braiding, coalescence and connection.The complexity of landslide moving path increases landslide risk.Therefore, researches on the quantifications and probability distributions of the complexities of landslide moving paths are required for landslide hazard assessment.In this paper it systematically reviews current researches on the complexities of landslide moving paths, points out key problems faced by relevant researches, and proposed perspectives for future researches.Generally, both the quantifications and probabilistic distributions of the complexities of landslide moving paths are inadequate.Specifically, the current profile abstraction method for landslide moving path is not applicable to multi-path complex behaviors; existing indices cannot systematically and scientifically quantify the complexities of landslide moving paths; the probability distribution functions of the complexities of landslide moving paths and their major constraining factors are not clear.Further, for solving the above problems, in this paper it suggests in the prospects: (1) to realize profile abstractions of multi-path complex behaviors mainly by transforming multi-paths into single-paths section by section; (2) to systematically quantify the complexities of landslide moving paths by developing a profile based index system; (3) to find out the probability distribution functions of the complexities of landslide moving paths and their major constraining factors by comprehensively analyzing data of landslide cases from various sources; and finally to develop prediction models for the probability distributions of the complexities of landslide moving paths, and further give a scientific support for quantitative landslide hazard and risk assessments in practice.
-
Key words:
- landslide /
- moving path /
- complexity /
- probability distribution /
- profile /
- engineering geology
-
0. 引言
我国大陆地区将地质灾害分为崩塌、滑坡、泥石流、地面塌陷、地裂缝和地面沉降等.因此,在狭义上来讲,滑坡是与崩塌和泥石流等相区别的地质灾害类型.我们也通常将英文“Landslide”译为“滑坡”.然而,国际上“Landslide”这一术语指“土、石、泥或碎屑等物质在重力的主要作用下的运动”,并按物质组成与运动形式等进行了系统性的分类(例如,Varnes, 1958, 1978;Cruden,1991;Cruden and Varnes, 1996;Hungr et al., 2001, 2014;Cruden and Lan, 2015).这一指代更接近“slope movement”的表义(Varnes,1978),包括了中文语境中的“崩塌”“滚石”“落石”“滑坡”“泥石流”“碎屑流”“滑坡-碎屑流”“岩崩”等多种形式的灾害.因此,滑坡这一概念也有更广义的指代.本文采用广义的滑坡概念,除狭义的滑坡,也涵盖了泥石流与碎屑流等灾害类型.
滑坡(Landslide)是发生数量最大、分布最广的地质灾害(中国地质环境监测院(自然资源部地质灾害技术指导中心),2019.全国地质灾害通报,北京;周超等,2020).一方面,在当前地震频发、气候快速变化,特别是人类活动增强的背景下,滑坡发生的时空频率和规模呈现出增长趋势;另一方面,人口增长与社会经济快速发展导致滑坡引起的潜在人员伤亡和经济损失加大(例如,Gariano and Guzzetti, 2016;Froude and Petley, 2018;Fan et al., 2019;Haque et al., 2019;柴波等,2020;Huang et al., 2021).因此,滑坡危险性和风险评估,对国家和地区的防灾减灾有重要意义.滑坡影响范围预测是滑坡危险性评估的关键内容之一,而滑坡运动路径决定了滑坡影响范围.因此,研究滑坡运动路径对滑坡危险性评估有重要意义.
滑坡作为一种在多种复杂因素共同作用下发生的自然过程,其运动路径具有天然的复杂性属性.自然滑坡的真实运动路径与简单滑块倚重力沿平整斜坡向下运动的理想路径具有显著差别.因此,作为一种普遍存在的内在属性,复杂性成为滑坡运动路径研究的不可或缺的重要内容之一.然而,当前国内外有关滑坡运动路径复杂性的研究仍处于零散状态(例如,Criss et al., 2020;Li et al., 2020;樊晓一等,2020;王丽娟等,2020;He et al., 2021;Schaefer et al., 2021),对相关研究现状缺少系统性的梳理和总结,对相关研究趋势缺少系统性的分析和展望.
本文首先介绍了滑坡运动路径复杂行为的主要类型,并详细探讨了滑坡路径复杂度的重要意义.在全面检索与收集国内外相关研究文献的基础上,系统地梳理和总结了滑坡运动路径复杂度的研究现状,并指出了相关研究所面临的关键问题.最后,针对如何解决滑坡运动路径复杂度研究面临的关键问题进行了展望.
1. 研究背景
1.1 滑坡运动路径复杂行为的类型
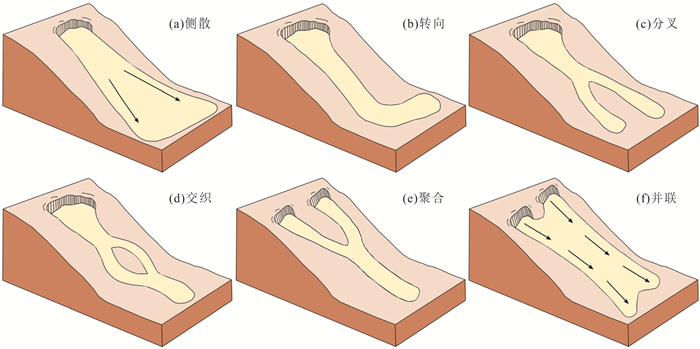
滑坡运动路径的复杂性体现在多种行为上.综合已有的有关滑坡运动路径描述的研究(Nicoletti and Sorriso-Valvo, 1991;Brunetti et al., 2014;Bessette-Kirton et al., 2020;Li et al., 2021;Schaefer et al., 2021),本文总结出6种普遍存在的、基本的滑坡运动路径复杂行为,如图 1所示,分别为:(1)侧散(spreading);(2)转向(turning);(3)分叉(splitting);(4)交织(braiding);(5)聚合(coalescence);(6)并联(connection).
 图 1 滑坡运动路径的6种基本复杂行为示意图(改自Schaefer et al., 2021)Fig. 1. Sketches showing the 6 fundamental complex behaviors of landslide moving paths (modified from Schaefer et al., 2021)
图 1 滑坡运动路径的6种基本复杂行为示意图(改自Schaefer et al., 2021)Fig. 1. Sketches showing the 6 fundamental complex behaviors of landslide moving paths (modified from Schaefer et al., 2021)其中,侧散与转向为“单路径”复杂行为,而分叉、交织、聚合与并联等则为“多路径”复杂行为.单个滑坡一般以某一种运动路径复杂行为为主,也有可能集多种复杂行为于一体;而在地震与降雨等事件触发的滑坡群中,由于边坡失稳与滑坡大面积发生,滑坡更有可能集多种复杂行为于一体.
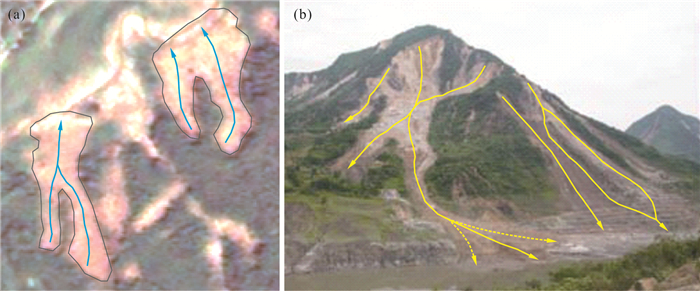
运动路径的复杂行为在自然滑坡中普遍存在.滑坡运动路径复杂行为的典型案例包括:四川茂县新磨村滑坡在末端产生侧散行为(例如,Huang et al., 2019);云南镇雄高坡村滑坡具有明显的转向行为(例如,Yin et al., 2017);四川都江堰三溪村滑坡在失稳后产生分叉并且具有一定的转向行为(例如,Gao et al., 2017);贵州水城坪地村滑坡则具有明显的交织行为(例如,Guo et al., 2020);福建南平强降雨触发滑坡具有聚合与并联等多种复杂行为(图 2a);而造成山河破碎的汶川地震所触发的滑坡,其路径复杂行为则更加多样,仅单个滑坡就可集聚合、分叉、转向、侧散等复杂行为于一身(例如,Yin et al., 2009;图 2b).
 图 2 滑坡运动路径的6种基本复杂行为的典型案例a.福建南平强降雨触发滑坡群;b.汶川地震触发滑坡群(改自Yin et al., 2009)Fig. 2. Typical cases of the 6 fundamental complex behaviors of landslide moving paths
图 2 滑坡运动路径的6种基本复杂行为的典型案例a.福建南平强降雨触发滑坡群;b.汶川地震触发滑坡群(改自Yin et al., 2009)Fig. 2. Typical cases of the 6 fundamental complex behaviors of landslide moving paths1.2 滑坡运动路径复杂度研究的意义
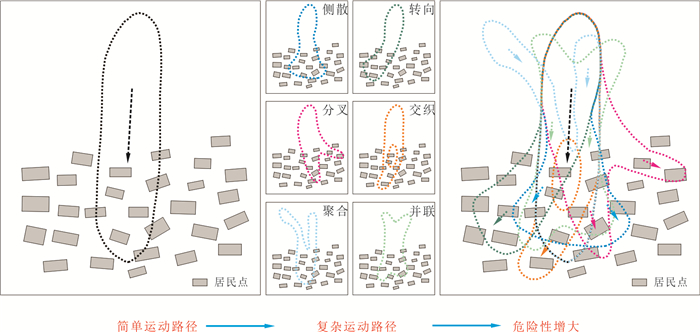
滑坡危险性在传统上包括三大要素:时间、空间与规模(例如,Guzzetti et al., 2005;Jaiswal et al., 2010;胡瑞林等,2013).然而,滑坡运动路径的复杂性也可增大滑坡的危险性.如图 3所示,滑坡运动路径的复杂性增大了滑坡运动路径的不确定性,进而增大了滑坡危险性预测与灾前防控的难度.路径复杂与高度不确定的灾害,相比路径简单易预测的灾害,危险性更大(Tsuchida et al., 2019).
实际的滑坡案例也反映了运动路径的复杂行为增大了滑坡的危害性.例如:四川茂县新磨村滑坡不但掩埋了其源区正下方的新磨村,其在末端的侧散行为也造成了新磨村西北侧的若干房屋损毁(Huang et al., 2019);云南镇雄高坡村滑坡的转向行为使其下方多个村庄都处于风险之中(Yin et al., 2017);四川都江堰三溪村滑坡的分叉行为使其左侧沟谷中的居民点也受到威胁(Gao et al., 2017);贵州水城坪地村滑坡的交织行为则造成判断其下方受威胁居民点的难度增大(Guo et al., 2020).
基于滑坡运动路径复杂性可增大滑坡危险性的认识,本文提出滑坡运动路径复杂度,作为重要补充,是除时间、空间和规模之外,滑坡危险性评估的关键要素之一.因此,滑坡运动路径复杂度应纳入滑坡危险性评估之中,具有重要的研究意义.
需要指出的是,基于过程模拟的灾害危险性评估可同时实现灾害影响范围与强度规模的预测(例如,Lan et al., 2013;仉义星等,2019);对灾害影响范围的模拟事实上同时实现了对灾害空间分布与运动路径复杂度的评估.但是,在更多情况下,特别是在区域性评估工作中,滑坡空间分布评估仅给出空间位置上滑坡发生可能性的高低,并不给出滑坡运动路径的预测.因此,滑坡运动路径复杂度评估仍然是通用滑坡危险性评估的重要补充.
另外,滑坡运动路径复杂度与滑坡空间分布之间具有一定相关性,二者并非完全独立.事实上,滑坡时间、空间与规模之间也并非完全独立;有众多因素,比如降雨强度,同时影响着滑坡发生的时间、空间和规模.因此,一定的相关性不影响时间、空间、规模与运动路径复杂度同时作为滑坡危险性评估的关键要素.
1.3 滑坡运动路径复杂度研究的内容需求
作为滑坡危险性评估的关键要素之一,滑坡运动路径复杂度面临以下具体的研究需求.
1.3.1 滑坡运动路径复杂度的量化
对滑坡运动路径复杂度进行量化,也即:发展一套复杂度的计算方法,用来定量描述复杂行为的复杂程度,以反映复杂行为带来的危害程度,是将运动路径复杂度纳入滑坡危险性评估的根本前提.以滑坡规模作为类比,也同样需要对滑坡规模进行量化,以表征滑坡的潜在危害程度.从更严格的意义上来讲,滑坡规模是对滑坡强度的描述,综合大小、位移和速度等特征,可反映滑坡的破坏能力.也有许多研究使用大小(面积与体积)来量化规模;如此,便可在滑坡危险性评估中使用滑坡大小来反映滑坡危害程度.因而,从反映危害程度这一需求出发,滑坡运动路径复杂度的量化是其纳入滑坡危险性评估的根本前提.
1.3.2 滑坡运动路径复杂度的概率分布
滑坡危险性评估即推知特定时间段内、特定区域中,产生特定危害的概率.滑坡危险性(H)在传统上是时间概率(PT)、空间概率(PS)与规模概率(PM)三者的联合概率,也即表达为三者的乘积(图 4).新补充滑坡运动路径复杂度这一要素之后,滑坡危险性表达为时间概率(PT)、空间概率(PS)、规模概率(PM)与运动路径复杂度概率(PC)四者的联合概率(图 4).也即,评估滑坡危险性就是评估滑坡的时间概率、空间概率、规模概率和运动路径复杂度概率.
滑坡的时间、空间和规模概率的评估各有常用方法.时间概率通常根据触发事件比如降雨或地震的重现期进行评估(例如,Lan et al., 2013;伍宇明等,2014);空间概率通常根据不同灾害因子的敏感性的空间分布进行评估(例如,兰恒星等,2002;Lan et al., 2004;Li et al., 2017;李郎平等,2017);规模概率通常基于滑坡规模的概率分布进行评估(例如,Li et al., 2014, 2016),也即根据研究区的滑坡规模概率分布函数来评估特定规模滑坡的发生概率.
运动路径复杂度是对滑坡整体特征的描述,无法在具体空间位置上,比如栅格单元上,对其进行描述评估.类似地,滑坡规模也是描述滑坡的整体特征,其概率评估是在整个研究区之内进行.因此,滑坡运动路径复杂度的概率评估可以参考规模概率的评估方式.根据研究区的滑坡运动路径复杂度概率分布函数,来估计特定复杂度的发生概率(图 4),这就首先要求对复杂度的概率分布进行预测.因此,从应用的角度来讲,研究并预测滑坡运动路径复杂度的概率分布,是其纳入滑坡危险性评估的必然需求.
2. 研究综述
2.1 滑坡运动路径研究的文献统计分析
作者利用中国知网(CNKI)和Web of Science文献数据库,使用“滑坡”“运动”与“路径”等关键词的所有可能组合作为主题检索词(表 1和表 2),对相关中文和英文文献进行了检索.
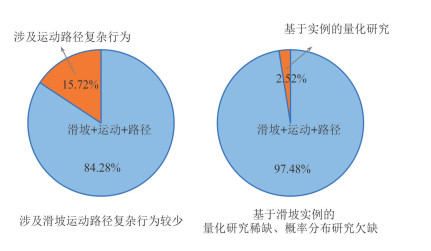
表 1 滑坡运动路径研究文献中国知网(CNKI)数据库中文主题检索词Table Supplementary Table Chinese searching keywords for literatures about researches on landslide moving paths in China National Knowledge Infrastructure (CNKI)主题检索词1 主题检索词2 主题检索词3 滑坡 运动 路径 泥石流 滑动 轨迹 碎屑流 流动 N.A. N.A. 运移 N.A. 表 2 滑坡运动路径研究文献Web of Science数据库英文主题检索词Table Supplementary Table English searching keywords for literatures about researches on landslide moving paths in Web of Science主题检索词1 主题检索词2 “landslide” “landslide path” “debris flow” “mo* path” (i.e., moving path, movement path, motion path) “rock avalanche” “*out path” (i.e., runout path, run-out path) “debris avalanche” “slid* path” (i.e., slide path, sliding path) N.A. “flow* path” (i.e., flow path, flowing path) 注:使用“route”替换“path”进行检索几乎不返回结果. 检索发现,总共有150多篇中文和英文文献的主题词包含了“滑坡”“运动”与“路径”等关键词的组合.然而,在检索结果文献中,仅有25篇直接或间接地涉及了滑坡运动路径的复杂行为,不到总数的1/6(图 5).研究内容主要包括:
(1) 描述具体滑坡实例的运动路径复杂特征(例如,Lan et al., 2008;Xing et al., 2015, 2016, 2017;Dufresne et al., 2016;McDougall,2017;Michelini et al., 2017;Imaizumi et al., 2019;Tsuchida et al., 2019;Guo et al., 2020;王丽娟等,2020;Schaefer et al., 2021);
(2) 使用模拟手段分析滑坡运动路径的复杂变化(例如,D’Ambrosio et al., 2003;Dai et al., 2014;杜娟等,2015;王玉峰等,2016;Cuomo et al., 2017;Kattel et al., 2018;张涛等,2019;周礼等,2019;Chae et al., 2020).
在检索结果中,仅有少数研究利用简单的参数对滑坡实例的运动路径特征进行了一定的定量分析(例如,Schneider et al.2011;Brideau et al., 2019;胡晓波等,2019;樊晓一等,2020),占检索结果文献总数的2.52%(图 5).
总体上,当前关注滑坡运动路径复杂行为的研究文献较少,量化研究稀缺,概率分布研究欠缺(图 5).以下,就量化和概率分布两个方面的相关文献进行更详细的介绍.
2.2 滑坡运动路径复杂行为的量化和概率分布研究
最常见的对滑坡运动路径的定量描述是长度,也即滑坡的运动距离(例如,Cruden and Varnes, 1996;Lan et al., 2008;詹威威等,2017;樊晓一等,2020;Li et al., 2020;Gao et al., 2021).然而,仅仅使用长度并不能描述滑坡运动路径的复杂行为.
在有关滑坡运动路径复杂行为的研究中,Schaefer et al.(2021)分析了泥石流的复杂“变向行为”(avulsion;包括分流、分叉、散布、交织、转向)的特征及其影响因素.然而,该研究只简单地分析了不同变向行为的有利因素,并未对变向行为进行量化描述与分析.事实上,即使是相同的变向行为,其变向程度也有一定的差别.例如,同样是转向行为,转向的角度可有大小之分,转向的位置也有前后之分.并且,具体的某个泥石流可具有多种变向行为,不能简单归为某一种变向类型.胡晓波等(2019)将滑坡运动路径纵剖面形态分为凸面型、阶梯型、凹面型、平直型4类,评价了其对滑坡-碎屑流运动能量消耗的影响,但仍未对路径复杂行为进行定量描述.
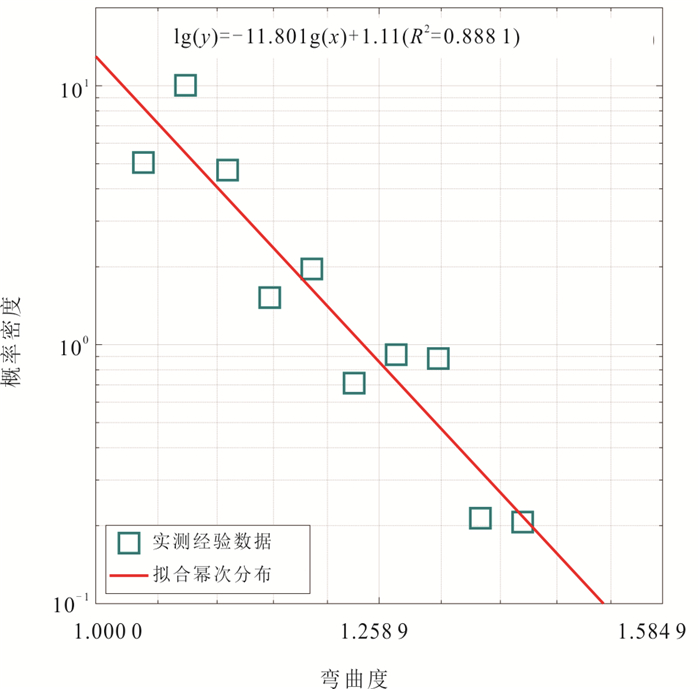
有少数研究对滑坡运动路径复杂行为进行了定量描述.在提出使用“剖面线(profile)”来概化滑坡运动路径的基础上,Li et al.(2020)进一步提出了“弯曲度(tortuosity)”作为描述滑坡运动路径特征的定量参数之一.弯曲度为滑坡运动路径的总长度与路径起讫点之间的直线位移的比值(L/D;图 6).滑坡的真实运动路径可概化为三维空间中的折线,因此其总长度一定比路径起讫点之间的直线位移大;也即,弯曲度的值在理论上总大于1.弯曲度与Schneider et al.(2011)提出的“路径偏离指数(path deviation index)”本质上类似,但具有更加完备的定义.通常,在运动路径总长度一定的情况下,转向角度越大、转向次数越多,弯曲度也越大.尽管弯曲度可在一定程度上定量描述滑坡运动路径的转向复杂行为,但是仍然未见对侧散、分叉、交织、聚合与并联等其他类型的路径复杂行为的定量描述研究.
总体上,当前滑坡运动路径复杂行为的量化研究依然稀缺(图 5),而限制量化研究的主要难点在于缺少有效的复杂度量化手段.
滑坡运动路径复杂行为的量化研究的稀缺,进一步导致概率分布研究的欠缺.在提出“弯曲度(tortuosity)”这一与滑坡运动路径复杂行为相关的定量参数后,Li et al.(2020)也利用直方图展示了弯曲度这一参数的频率分布.典型案例分析结果表明,弯曲度可符合幂次分布(图 7).然而,总体上,滑坡运动路径复杂行为的概率分布研究仍然欠缺(图 5).仍需在量化侧散、转向、分叉、交织、聚合与并联等路径复杂行为的基础上,进行各量化参数的概率分布研究.
3. 关键问题
本节基于以上国内外研究现状的总结,详细分析和指出相关研究所面临的关键问题.
3.1 滑坡运动路径的剖面线概化
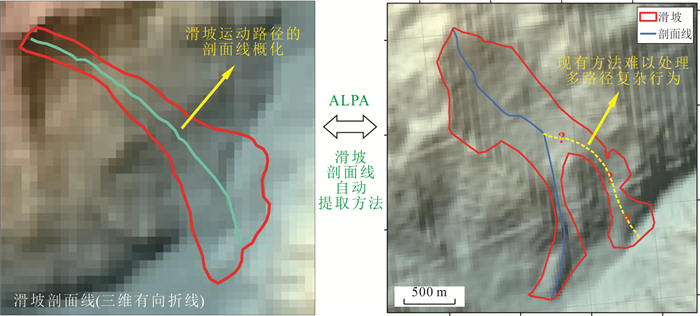
滑坡的真实运动路径覆盖一定的地表空间范围.使用“剖面线(profile)”对路径进行概化,可为描述特别是定量描述路径特征提供明确的靶标对象.剖面线是滑坡运动路径的中心线,实际上是使用“有向折线”概化地代表了滑坡的运动路径(图 8).因此,利用剖面线概化滑坡运动路径,并定量描述其复杂特征,是突破滑坡运动路径复杂度量化难题的有效手段.然而,现有滑坡运动路径的剖面线概化方法仍面临难以处理多路径复杂行为的关键技术问题.
对于崩塌滚石这类单个岩块独立地沿斜坡滚落运动的灾害,在将灾害体抽象为质点之后,其运动路径本身就是有向折线(例如,Lan et al., 2007, 2010, 2015;Li and Lan, 2015).然而,对于覆盖一定地表范围的滑坡,其运动路径的剖面线概化面对很大挑战.
使用人工手动的方法进行滑坡剖面线的描画,一方面耗时耗力,另一方面会带来难以控制的主观因素.因此,需要发展一种通用的滑坡剖面线自动提取方法.有研究展示出可以利用地震监测网反演的受力过程计算出大型滑坡的滑坡路径(Zhao et al., 2020),然而这一方法的推广应用受到限制.也有相关的研究通过在滑坡多边形中拟合一条折线来形成滑坡的“长度线”(Golovko et al., 2017),然而该方法并不能处理滑坡在末端产生爬升等复杂情况.
作者基于多级分割与连接滑坡高程点的思路提出了一种滑坡剖面线的自动提取方法,并形成了开源脚本ALPA(Li et al., 2020),其所提取的剖面线代表了滑坡运动中心线.然而,这一方法虽能合理地处理具有侧散和转向等单路径复杂行为的滑坡(图 8),当前仍然难以处理具有分叉、交织、聚合与并联等多路径复杂行为的滑坡(图 8).
因此,完善现有滑坡运动路径的剖面线概化方法(剖面线自动提取方法),以适用于多路径复杂滑坡,是相关研究亟待解决的第一个关键技术问题.
3.2 滑坡运动路径复杂度的量化
如何度量滑坡运动路径的侧散、转向、分叉、交织、聚合与并联等复杂行为并不是一个简单的问题.这涉及到两个层次的问题:一是如何定义复杂度指标以从定量的角度科学合理地反映滑坡运动路径的复杂程度?二是如何基于剖面线计算所提出的复杂度指标?
首先,单种滑坡运动路径复杂行为面临着定量指标的选取问题.例如,对于转向行为,仅度量转向角度并不足以反映转向复杂性.转向角度相同,转向位置可以不同.另外,转向次数也需要考虑.例如,侧散行为并不只是发生在滑坡的末端,也可发生在滑坡的中部、甚至源区附近等位置,因而侧散程度与侧散位置都需要考虑.再例如,对于分叉行为,也需同时考虑分叉位置与分叉个数等特征来综合反映复杂度.因而,单种行为的复杂度指标应该是运动路径(剖面线)的多项特征指标的综合(图 9).
其次,单个滑坡也可以集多种复杂行为于一体(图 2b).因此,滑坡运动路径的整体复杂度应为多种行为的复杂度指标的综合.从而,滑坡运动路径复杂度的科学量化需要一套从“剖面线特征指标”到“单行为复杂度指标”再到“多行为综合复杂度指标”的多层级指标体系(图 9).
然而,当前仅有零星的研究提出了反映滑坡运动路径复杂度的指标,远未形成系统性的指标体系.如上所述,作者使用“弯曲度(tortuosity)”定量描述了滑坡运动路径的特征(Li et al., 2020).但是,弯曲度单独并不足以全面反映转向复杂度;在总体弯曲度相同的情况下,滑坡运动路径在局部的转向次数与转向角度等可以不同.具体构建指标体系时,各级指标的选择、计算与综合等,皆面临未知挑战.
总体上,现有的零星的指标不能满足滑坡运动路径复杂度的系统性科学量化.因此,构建一套多层级指标体系,以系统地科学量化滑坡运动路径复杂度,是相关研究亟待解决的第二个关键技术问题.
3.3 滑坡运动路径复杂度的概率分布
滑坡运动路径复杂度的概率分布研究,其最终目的是进行概率分布的预测.概率分布的预测,具体来讲,是在已知概率分布的分布函数的基础上,预测概率分布的参数.例如,对于正态分布就是预测均值和方差,对于伽马分布就是预测形状参数与尺度参数.在已知滑坡运动路径复杂度概率分布的分布函数及其对应的参数后,即可估计研究区内特定复杂度的发生概率(图 4).
预测滑坡运动路径复杂度的概率分布,其意义在于:即使对相同的研究区,在不同的未来情境下,比如在不同的地震与降雨等触发条件下,也会发生不同的滑坡、产生不同的滑坡运动路径复杂度概率分布,进而导致不同的滑坡危险性.因此,研究滑坡运动路径复杂度的概率分布,建立其预测模型,预测不同区域、不同未来情境下,滑坡运动路径复杂度的概率分布,进而估计特定复杂度的发生概率,是滑坡危险性评估的必然需求.然而,当前,滑坡运动路径复杂度的概率分布研究仍面临两个关键科学问题.
3.3.1 滑坡运动路径复杂度概率分布的分布函数不明
在滑坡危险性的四概率联合表达中,时间概率与空间概率通常分别通过触发事件重现期和因子敏感性空间分布来计算,而规模概率与运动路径复杂度概率则皆通过概率分布函数来计算(图 4).
对于滑坡规模概率分布(频率分布),国内外绝大多数研究表明,滑坡规模的概率在一定规模阈值以上随规模增大呈幂次递减(例如,许强和黄润秋,1997;Dai and Lee, 2001;Stark and Hovius, 2001;Malamud et al., 2004;Brunetti et al., 2009;Zhuang et al., 2010;姚令侃等,2010;胡元鑫等,2011;Xu et al., 2014;彭令等,2014;Zhou et al., 2015;Li et al., 2016;Tang et al., 2016;邱海军等,2016;Tanyaş et al., 2017).如以概率密度分布表示,这种分布形式在双对数图上呈现为一个长的“幂次尾部”和一个在小滑坡端的“拐点”(图 4).对于这一分布形式,学术界最常用的拟合分布函数为“双帕累托函数”(Stark and Hovius, 2001)和“反伽马函数”(Malamud et al., 2004).在有明确的分布函数进行拟合描述的前提下,滑坡规模概率分布已经被众多研究应用于滑坡危险性评估之中(例如,Guzzetti et al., 2005;Das et al., 2011).
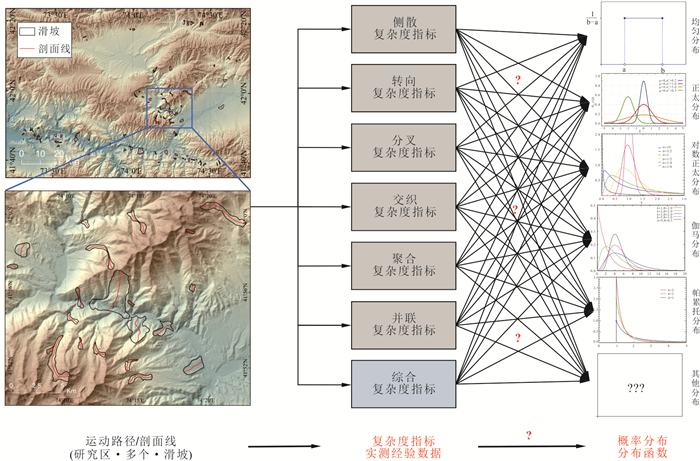
然而,当前适用于描述滑坡运动路径复杂度概率分布的分布函数仍然不明,导致其缺少应用于滑坡危险性评估的数学基础.根本地,只有在给出各个复杂度指标(包括单行为复杂度指标以及多行为综合复杂度指标)概率分布的分布函数之后(图 10),才能基于分布函数来估计特定复杂度的概率.典型案例分析表明,剖面线“弯曲度(tortuosity)”的概率密度可符合幂次分布(图 7).然而,众多复杂度指标所适用的分布函数仍然不明.各复杂度指标的概率分布符合哪种已知的分布函数,或者是否需要引入新的分布函数?这些都有待确定(图 10).
因此,确定适用于描述滑坡运动路径复杂度概率分布的分布函数,以奠定其纳入滑坡危险性评估的数学基础,是相关研究亟待解决的第一个关键科学问题.
3.3.2 滑坡运动路径复杂度概率分布的主控因素不清
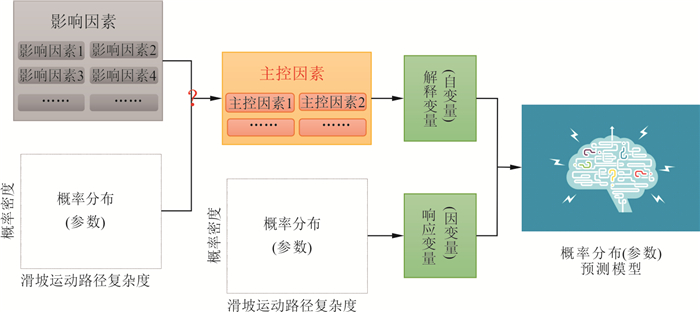
认识滑坡运动路径复杂度概率分布的主控因素,是建立其预测模型的基础.这是因为,只有在识别主控因素的基础之上,才能从主控因素中找出预测模型的解释变量(因变量)(图 11).基于类似原因,对于滑坡规模概率分布,已有众多研究分析了不同因素的影响控制作用,包括触发因素(例如,Chen,2009;Ghosh et al., 2012;Tanyaş et al., 2017)、岩性(例如,Iwahashi et al., 2003;Guzzetti et al., 2008;Hurst et al., 2013;Guo et al., 2017)和地形(例如,Hungr et al., 2008;Qiu et al., 2018)等.
滑坡运动路径的影响控制因素同样复杂.例如,在直觉上:规模越大,滑坡将运动更远,运动路径复杂化的可能性也更高;地形越复杂,滑坡运动路径一般也更复杂;滑坡组成物质的流动性越强,其运动路径越有可能复杂化.也有研究表明,滑坡几何特征与触发因素紧密相关(Rana et al., 2021).
尽管,有若干研究表明,地形(例如,Dai et al., 2014;Dufresne et al., 2016;王玉峰等,2016;Michelini et al., 2017;胡晓波等,2019;张涛等,2019;周礼等,2019;Chae et al., 2020;樊晓一等,2020)、规模(例如,Xing et al., 2015;Chae et al., 2020;樊晓一等,2020)、障碍物(例如,Cuomo et al., 2017;Kattel et al., 2018)以及滑坡物质动力学特征、岩性和基底物质等其他因素(例如,Dufresne et al., 2016;Imaizumi et al., 2019)可影响滑坡运动路径的复杂特征.然而,当前滑坡运动路径复杂度概率分布的主控因素仍然不清,特别是缺乏基于实例的多因素系统性挖掘分析.哪些因素对滑坡运动路径复杂度概率分布起主要控制作用?不同复杂度指标概率分布的主控因素是否有一定差别?仍然有待认识(图 11).
因此,识别滑坡运动路径复杂度概率分布的主控因素,以奠定其预测模型建立的解释变量基础,是相关研究亟待解决的第二个关键科学问题.
4. 研究展望
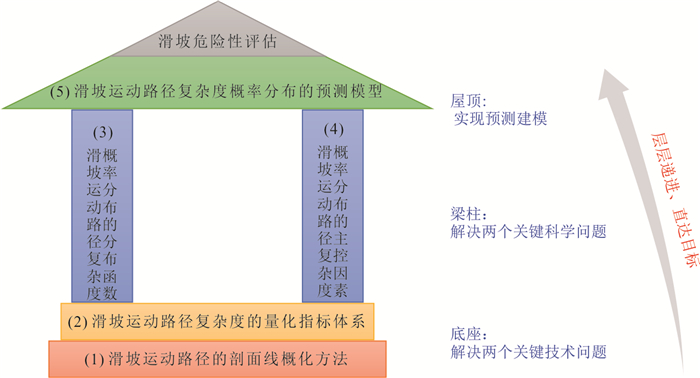
为解决以上滑坡运动路径复杂度研究所面临的关键问题,并实现支撑滑坡危险性评估的目标,本文建议在未来滑坡运动路径复杂度研究中关注5个内容:首先研发完善滑坡运动路径的剖面线概化方法,并构建基于剖面线的滑坡运动路径复杂度的量化指标体系;在实现复杂度量化的基础上,依次开展复杂度概率分布的分布函数和主控因素研究,最终建立复杂度概率分布的预测模型.建议的五个研究内容构成一个“层层递进、直达目标”的有机房屋结构:“底座”解决两个关键技术问题,“梁柱”解决两个关键科学问题,“屋顶”实现预测建模(图 12).以下对各建议研究内容的可行的实施思路进行简要展望.
(1) 完善滑坡运动路径的剖面线概化方法. 发展滑坡剖面线自动提取方法,主要完善现有方法,使其具备提取“分叉”、“交织”、“聚合”与“并联”等多路径复杂行为的能力.作者提出的现有滑坡剖面线自动提取方法ALPA采用了多级分割与连接滑坡高程格点的思路;将最终的所有高程格点子集相连,形成剖面线(Li et al., 2020).首先,根据高程格点子集的空间连续性、边界分布以及扩散特征对复杂行为进行区分,甄别出分叉、聚合、并联、交织等多路径复杂行为,以及侧散、转向等单路径复杂行为.其次,针对各多路径复杂行为类型,分别设计方案进行分段单路径化,随后利用现有方法分段提取进而合并形成剖面线.最终,解决现有方法不能处理多路径复杂行为的问题,为路径复杂度的指标体系量化奠定基础.
(2) 构建滑坡运动路径复杂度的量化指标体系. 首先,根据侧散、转向、分叉、交织、聚合与并联等复杂行为的具体特点,对各个复杂行为有针对性地选择各自适用的剖面线特征指标,进行计算方法定义与综合,进而为各个行为分别单独构建复杂度的量化指标.侧散复杂度指标可包括侧散位置、侧散比例、侧散偏度等;转向复杂度指标可包括转向次数、转向位置、转向角度等;分叉复杂度指标可包括分叉位置、分叉个数、分叉长短等;交织复杂度指标可包括交织位置、交织个数、交织面积等;聚合复杂度指标可包括聚合位置、聚合个数、聚合长短等;并联复杂度指标可包括并联个数、并联位置、并联规模等.另外,明确各量化指标与滑坡危险性的关系,进而对量化指标进行合理的调整与筛选,有助于使滑坡运动路径复杂度在滑坡危险性评估中发挥更大作用.可针对每个复杂度量化指标,基于滑坡实例数据,分析其与滑坡威胁范围等的关系,从而反映其与滑坡危险性的关系.其次,主要利用层次分析法(AHP),并且结合专家经验,确定各级指标的权重;综合各单行为复杂度指标,构建一个描述滑坡整体的运动路径多行为综合复杂度指标.最终,形成一套从剖面线特征指标,到单行为复杂度指标,到多行为综合复杂度指标的多层级指标体系,实现滑坡运动路径复杂度的系统性科学量化,为滑坡运动路径复杂度的概率分布研究奠定基础.
(3) 确定滑坡运动路径复杂度概率分布的分布函数. 选择若干典型的滑坡数据集,包括长时间跨度的历史数据集与地震和降雨等事件触发的数据集,作为探索滑坡运动路径复杂度的概率分布规律的经验数据.提取各数据集中各滑坡的剖面线,进而求取各滑坡的运动路径复杂度数据.根据各实例数据集的滑坡运动路径复杂度经验数据,针对每个滑坡运动路径复杂度指标,主要利用直方图以及累积频率图等数据探测方法,筛查可能适用的候选分布函数,例如均匀分布、正态分布、对数正态分布、帕累托分布等.进一步,使用经验数据进行候选分布函数的参数拟合与假设检验,使用赤池信息量准则(AIC)、KS检验等判断各候选分布函数对实测经验数据的拟合优良度,确定描述各个复杂度指标的最优分布函数,为滑坡运动路径复杂度概率分布的预测建模与滑坡危险性评估应用奠定数学基础.
(4) 识别滑坡运动路径复杂度概率分布的主控因素. 收集各滑坡实例数据集所对应的地形地貌、地质构造、气象水文、土壤植被和人类活动等方面的滑坡影响因素数据,包括地震与降雨等触发事件的数据.首先,基于滑坡实例影响因素数据和运动路径复杂度实测经验数据,利用主成分分析、因子分析等数据挖掘方法,分析各因素与滑坡运动路径复杂度之间的相关关系,筛选出复杂度的主要影响因素,为复杂度概率分布主控因素的识别奠定基础.进而,具体通过对比不同数据集与数据子集之间各个复杂度概率分布(参数)的差异,利用地理探测器、LASSO算法(套索算法)和统计显著性分析等方法,找出造成显著差异的影响因素,标记为各复杂度概率分布的主控因素,进而为复杂度概率分布的预测建模奠定基础.
(5) 建立滑坡运动路径复杂度概率分布的预测模型. 根据滑坡运动路径复杂度概率分布的主控因素,准备预测模型的解释变量.对于不同触发因素,分开建立触发因素的解释变量.例如,地震滑坡的触发因素解释变量为地面峰值加速度或地震烈度等,降雨滑坡的触发因素解释变量为降雨强度等.首选,使用在滑坡风险评估中常用的方差扩大因子(variance inflation factor)和皮尔逊积矩相关系数(pearson correlation coefficient)等方法(Dormann et al., 2013;Bui et al., 2016),分析各解释变量之间的多重共线性,进而去除与其他变量共线性较大的解释变量.进而,使用多元回归、决策树、随机森林、支持向量机以及人工神经网络等方法,根据实例数据建立各复杂度概率分布(参数)与解释变量之间的定量关系,实现滑坡运动路径各复杂度概率分布的预测建模.在数据量不足时,使用蒙特卡洛模拟增加训练数据量.最后,基于典型的滑坡实例数据集进行模型的验证和优选,最终为支撑滑坡危险性定量评估奠定基础.
滑坡运动路径复杂度的相关研究成果,最终可在滑坡危险性评估工作中得到应用.生态文明建设、精准扶贫与异地搬迁等政策的实施,有利于减少山地灾害对人民生命和财产的威胁.另一方面,基于区域社会经济发展的需求,大量基础设施等重大工程在山区建设和运行,造成新的灾害风险.特别地,重大工程除关注其本身面临的灾害风险外,也必须高度关注其施工安全(例如,兰恒星等, 2016, 2021).在四川宁南白鹤滩水电站与福建泰宁池潭水电站,均发生灾害冲毁施工营地造成重大人员伤亡的事故.重大工程施工营地的选取,应加强考虑滑坡运动路径的复杂性(高度不确定性),提升滑坡危险性评估的全面性,以充分预判和应对灾害风险.
5. 结论
本文系统地梳理和总结了滑坡运动路径复杂度的研究现状,指出了相关研究所面临的关键问题,并进行了未来研究展望.
本文提出滑坡运动路径复杂度的概率预测是对滑坡危险性评估的重要补充,并指出量化和概率分布研究是将滑坡运动路径复杂度纳入滑坡危险性评估的根本前提和必然需求,具有重要的意义.
总体上,当前关于滑坡运动路径复杂度的研究,主要面临量化研究稀缺、概率分布研究欠缺的问题.具体表现为,两个关键技术问题:现有滑坡运动路径的剖面线概化方法难以处理多路径复杂行为、现有零星的指标不能满足滑坡运动路径复杂度的系统性科学量化;两个关键科学问题:滑坡运动路径复杂度概率分布的分布函数不明、主控因素不清.
针对以上待解决的关键问题,本文展望了未来研究内容及其实施思路:主要通过分段单路径化方案,实现滑坡运动多路径复杂行为的剖面线概化;构建基于剖面线特征描述的滑坡运动路径复杂度的量化指标体系,突破量化难题;基于大量滑坡实例数据的统计分析和规律挖掘,确定滑坡运动路径复杂度概率分布的分布函数、查清其主控因素;最终,实现滑坡运动路径复杂度概率分布的预测建模,支撑滑坡危险性及风险定量评估.
-
图 1 滑坡运动路径的6种基本复杂行为示意图(改自Schaefer et al., 2021)
Fig. 1. Sketches showing the 6 fundamental complex behaviors of landslide moving paths (modified from Schaefer et al., 2021)
图 2 滑坡运动路径的6种基本复杂行为的典型案例
a.福建南平强降雨触发滑坡群;b.汶川地震触发滑坡群(改自Yin et al., 2009)
Fig. 2. Typical cases of the 6 fundamental complex behaviors of landslide moving paths
表 1 滑坡运动路径研究文献中国知网(CNKI)数据库中文主题检索词
Table 1. Chinese searching keywords for literatures about researches on landslide moving paths in China National Knowledge Infrastructure (CNKI)
主题检索词1 主题检索词2 主题检索词3 滑坡 运动 路径 泥石流 滑动 轨迹 碎屑流 流动 N.A. N.A. 运移 N.A. 表 2 滑坡运动路径研究文献Web of Science数据库英文主题检索词
Table 2. English searching keywords for literatures about researches on landslide moving paths in Web of Science
主题检索词1 主题检索词2 “landslide” “landslide path” “debris flow” “mo* path” (i.e., moving path, movement path, motion path) “rock avalanche” “*out path” (i.e., runout path, run-out path) “debris avalanche” “slid* path” (i.e., slide path, sliding path) N.A. “flow* path” (i.e., flow path, flowing path) 注:使用“route”替换“path”进行检索几乎不返回结果. -
Bessette-Kirton, E. K., Coe, J. A., Schulz, W. H., et al., 2020. Mobility Characteristics of Debris Slides and Flows Triggered by Hurricane Maria in Puerto Rico. Landslides, 17(12): 2795-2809. https://doi.org/10.1007/s10346-020-01445-z Brideau, M. A., Stead, D., Millard, T. H., et al., 2019. Field Characterisation and Numerical Modelling of Debris Avalanche Runout on Vancouver Island, British Columbia, Canada. Landslides, 16(5): 875-891. https://doi.org/10.1007/s10346-019-01141-7 Brunetti, M. T., Guzzetti, F., Cardinali, M., et al., 2014. Analysis of a New Geomorphological Inventory of Landslides in Valles Marineris, Mars. Earth and Planetary Science Letters, 405: 156-168. https://doi.org/10.1016/j.epsl.2014.08.025 Brunetti, M. T., Guzzetti, F., Rossi, M., 2009. Probability Distributions of Landslide Volumes. Nonlinear Processes in Geophysics, 16(2): 179-188. https://doi.org/10.5194/npg-16-179-2009 Bui, D. T., Tuan, T. A., Klempe, H., et al., 2016. Spatial Prediction Models for Shallow Landslide Hazards: A Comparative Assessment of the Efficacy of Support Vector Machines, Artificial Neural Networks, Kernel Logistic Regression, and Logistic Model Tree. Landslides, 13(2): 361-378. https://doi.org/10.1007/s10346-015-0557-6 Chae, B. G., Wu, Y. H., Liu, K. F., et al., 2020. Simulation of Debris-Flow Runout near a Construction Site in Korea. Applied Sciences, 10(17): 6079. https://doi.org/10.3390/app10176079 Chai, B., Tao, Y. Y., Du, J., et al., 2020. Hazard Assessment of Debris Flow Triggered by Outburst of Jialong Glacial Lake in Nyalam County, Tibet. Earth Science, 45(12): 4630-4639(in Chinese with English abstract). Chen, C. Y., 2009. Sedimentary Impacts from Landslides in the Tachia River Basin, Taiwan. Geomorphology, 105(3-4): 355-365. https://doi.org/10.1016/j.geomorph.2008.10.009 Criss, R. E., Yao, W. M., Li, C. D., et al., 2020. A Predictive, Two-Parameter Model for the Movement of Reservoir Landslides. Journal of Earth Science, 31(6): 1051-1057. https://doi.org/10.1007/s12583-020-1331-9 Cruden, D, M., 1991. A Simple Definition of a Landslide. Bulletin of the International Association of Engineering Geology, 43(1): 27-29. https://doi.org/10.1007/bf02590167 Cruden, D, M., Varnes, D. J., 1996. Landslide Types and Processes. In: Turner, A. K., Schuster, R. L., eds., Landslides Investigation and Mitigation. National Academy Press, Washington, D. C., 36-75. Cruden, D., Lan, H. X., 2015. Using the Working Classification of Landslides to Assess the Danger from a Natural Slope. In: Lollino, G., ed., Engineering Geology for Society and Territory. Springer, Cham, Switzerland. https://doi.org/10.1007/978-3-319-09057-3_1 Cuomo, S., Cascini, L., Pastor, M., et al., 2017. Modelling the Propagation of Debris Avalanches in Presence of Obstacles. In: Mikoš, M., ed., Advancing Culture of Living with Landslides. Springer, Cham, Switzerland. https://doi.org/10.1007/978-3-319-53487-9_55 Dai, F. C., Lee, C. F., 2001. Frequency-Volume Relation and Prediction of Rainfall-Induced Landslides. Engineering Geology, 59(3-4): 253-266. https://doi.org/10.1016/s0013-7952(00)00077-6 Dai, Z. L., Huang, Y., Cheng, H. L., et al., 2014.3D Numerical Modeling Using Smoothed Particle Hydrodynamics of Flow-Like Landslide Propagation Triggered by the 2008 Wenchuan Earthquake. Engineering Geology, 180: 21-33. https://doi.org/10.1016/j.enggeo.2014.03.018 D'Ambrosio, D., Di Gregorio, S., Iovine, G., et al., 2003. First Simulations of the Sarno Debris Flows through Cellular Automata Modelling. Geomorphology, 54(1-2): 91-117. https://doi.org/10.1016/s0169-555x(03)00058-8 Das, I., Stein, A., Kerle, N., et al., 2011. Probabilistic Landslide Hazard Assessment Using Homogeneous Susceptible Units (HSU) along a National Highway Corridor in the Northern Himalayas, India. Landslides, 8(3): 293-308. https://doi.org/10.1007/s10346-011-0257-9 Dormann, C. F., Elith, J., Bacher, S., et al., 2013. Collinearity: A Review of Methods to Deal with it and a Simulation Study Evaluating Their Performance. Ecography, 36(1): 27-46. https://doi.org/10.1111/j.1600-0587.2012.07348.x Du, J., Yin, K. L., Wang, J. J., 2015. Simulation of Three-Dimensional Movement of Landslide-Debris Flow Based on Finite Volume Method. Chinese Journal of Rock Mechanics and Engineering, 34(3): 480-488(in Chinese with English abstract). Dufresne, A., Prager, C., Bösmeier, A., 2016. Insights into Rock Avalanche Emplacement Processes from Detailed Morpho-Lithological Studies of the Tschirgant Deposit (Tyrol, Austria). Earth Surface Processes and Landforms, 41(5): 587-602. https://doi.org/10.1002/esp.3847 Fan, X. M., Scaringi, G., Korup, O., et al., 2019. Earthquake-Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Reviews of Geophysics, 57(2): 421-503. https://doi.org/10.1029/2018rg000626 Fan, X. Y., Zhang, R. X., Hu, X. B., 2020. Study on the Influence of Valley Topographic Parameter on the Moving Distance of Landslide. Journal of Geomechanics, 26(1): 106-114(in Chinese with English abstract). Froude, M. J., Petley, D. N., 2018. Global Fatal Landslide Occurrence from 2004 to 2016. Natural Hazards and Earth System Sciences, 18(8): 2161-2181. https://doi.org/10.5194/nhess-18-2161-2018 Gao, L., Zhang, L. M., Chen, H. X., et al., 2021. Topography and Geology Effects on Travel Distances of Natural Terrain Landslides: Evidence from a Large Multi-Temporal Landslide Inventory in Hong Kong. Engineering Geology, 292: 106266. https://doi.org/10.1016/j.enggeo.2021.106266 Gao, Y., Yin, Y. P., Li, B., et al., 2017. Characteristics and Numerical Runout Modeling of the Heavy Rainfall-Induced Catastrophic Landslide-Debris Flow at Sanxicun, Dujiangyan, China, Following the Wenchuan Ms 8.0 Earthquake. Landslides, 14(4): 1361-1374. https://doi.org/10.1007/s10346-016-0793-4 Gariano, S. L., Guzzetti, F., 2016. Landslides in a Changing Climate. Earth-Science Reviews, 162: 227-252. https://doi.org/10.1016/j.earscirev.2016.08.011 Ghosh, S., van Westen, C. J., Carranza, E. J. M., et al., 2012. Generating Event-Based Landslide Maps in a Data-Scarce Himalayan Environment for Estimating Temporal and Magnitude Probabilities. Engineering Geology, 128: 49-62. https://doi.org/10.1016/j.enggeo.2011.03.016 Golovko, D., Roessner, S., Behling, R., et al., 2017. Automated Derivation and Spatio-Temporal Analysis of Landslide Properties in Southern Kyrgyzstan. Natural Hazards, 85(3): 1461-1488. https://doi.org/10.1007/s11069-016-2636-y Guo, C. W., Huang, Y. D., Yao, L. K., et al., 2017. Size and Spatial Distribution of Landslides Induced by the 2015 Gorkha Earthquake in the Bhote Koshi River Watershed. Journal of Mountain Science, 14(10): 1938-1950. https://doi.org/10.1007/s11629-016-4140-y Guo, J., Yi, S. J., Yin, Y. Z., et al., 2020. The Effect of Topography on Landslide Kinematics: A Case Study of the Jichang Town Landslide in Guizhou, China. Landslides, 17(4): 959-973. https://doi.org/10.1007/s10346-019-01339-9 Guzzetti, F., Ardizzone, F., Cardinali, M., et al., 2008. Distribution of Landslides in the Upper Tiber River Basin, Central Italy. Geomorphology, 96(1-2): 105-122. https://doi.org/10.1016/j.geomorph.2007.07.015 Guzzetti, F., Reichenbach, P., Cardinali, M., et al., 2005. Probabilistic Landslide Hazard Assessment at the Basin Scale. Geomorphology, 72(1-4): 272-299. https://doi.org/10.1016/j.geomorph.2005.06.002 Haque, U., da Silva, P. F., Devoli, G., et al., 2019. The Human Cost of Global Warming: Deadly Landslides and Their Triggers (1995—2014). The Science of the Total Environment, 682: 673-684. https://doi.org/10.1016/j.scitotenv.2019.03.415 He, X. L., Xu, C., Qi, W. W., et al., 2021. Landslides Triggered by the 2020 Qiaojia Mw 5.1 Earthquake, Yunnan, China: Distribution, Influence Factors and Tectonic Significance. Journal of Earth Science, 32(5): 1056-1068. https://doi.org/10.1007/s12583-021-1492-1 Hu, R. L., Fan, L. F., Wang, S. S., et al., 2013. Theory and Method for Landslide Risk Assessment-Current Status and Future Development. Journal of Engineering Geology, 21(1): 76-84(in Chinese with English abstract). doi: 10.3969/j.issn.1004-9665.2013.01.009 Hu, X. B., Fan, X. Y., Ma, X., 2019. Energy Consumption Evaluation of High-Speed and Long-Distance Landslide in Accelerated Motion. Yangtze River, 50(2): 191-196(in Chinese with English abstract). Hu, Y. X., Liu, X. R., Jiang, Y., et al., 2011. Three-Parameter Inverse-Gamma Probability Distribution Model of Incomplete Landslide Inventory. Journal of Central South University (Science and Technology), 42(10): 3176-3181(in Chinese with English abstract). Huang, D., Li, Y. Q., Song, Y. X., et al., 2019. Insights into the Catastrophic Xinmo Rock Avalanche in Maoxian County, China: Combined Effects of Historical Earthquakes and Landslide Amplification. Engineering Geology, 258: 105158. https://doi.org/10.1016/j.enggeo.2019.105158 Huang, Y. D., Xu, C., Zhang, X. L., et al., 2021. An Updated Database and Spatial Distribution of Landslides Triggered by the Milin, Tibet Mw 6.4 Earthquake of 18 November 2017. Journal of Earth Science, 32(5): 1069-1078. https://doi.org/10.1007/s12583-021-1433-z Hungr, O., Evans, S. G., Bovis, M. J., et al., 2001. A Review of the Classification of Landslides of the Flow Type. Environmental and Engineering Geoscience, 7(3): 221-238. https://doi.org/10.2113/gseegeosci.7.3.221 Hungr, O., Leroueil, S., Picarelli, L., 2014. The Varnes Classification of Landslide Types, an Update. Landslides, 11(2): 167-194. https://doi.org/10.1007/s10346-013-0436-y Hungr, O., McDougall, S., Wise, M., et al., 2008. Magnitude-Frequency Relationships of Debris Flows and Debris Avalanches in Relation to Slope Relief. Geomorphology, 96(3-4): 355-365. https://doi.org/10.1016/j.geomorph.2007.03.020 Hurst, M. D., Ellis, M. A., Royse, K. R., et al., 2013. Controls on the Magnitude-Frequency Scaling of an Inventory of Secular Landslides. Earth Surface Dynamics, 1(1): 67-78. https://doi.org/10.5194/esurf-1-67-2013 Imaizumi, F., Masui, T., Yokota, Y., et al., 2019. Initiation and Runout Characteristics of Debris Flow Surges in Ohya Landslide Scar, Japan. Geomorphology, 339: 58-69. https://doi.org/10.1016/j.geomorph.2019.04.026 Iwahashi, J., Watanabe, S., Furuya, T., 2003. Mean Slope-Angle Frequency Distribution and Size Frequency Distribution of Landslide Masses in Higashikubiki Area, Japan. Geomorphology, 50(4): 349-364. https://doi.org/10.1016/s0169-555x(02)00222-2 Jaiswal, P., van Westen, C. J., Jetten, V., 2010. Quantitative Landslide Hazard Assessment along a Transportation Corridor in Southern India. Engineering Geology, 116(3): 236-250. https://doi.org/10.1016/j.enggeo.2010.09.005 Kattel, P., Kafle, J., Fischer, J. T., et al., 2018. Interaction of Two-Phase Debris Flow with Obstacles. Engineering Geology, 242: 197-217. https://doi.org/10.1016/j.enggeo.2018.05.023 Lan, H. X., Derek Martin, C., Lim, C. H., 2007. Rockfall Analyst: A GIS Extension for Three-Dimensional and Spatially Distributed Rockfall Hazard Modeling. Computers & Geosciences, 33(2): 262-279. https://doi.org/10.1016/j.cageo.2006.05.013 Lan, H. X., Li, L. P., Wu, Y. M., 2015. Stochasticity of Rockfall Tracjectory Revealed by a Field Experiment Repeated on a Single Sample. In: Lollino, G., ed., Engineering Geology for Society and Territory. Springer, Cham, Switzerland. https://doi.org/10.1007/978-3-319-09057-3_304 Lan, H. X., Li, L. P., Zhang, Y. S., et al., 2013. Risk Assessment of Debris Flow in Yushu Seismic Area in China: A Perspective for the Reconstruction. Natural Hazards and Earth System Sciences, 13(11): 2957-2968. https://doi.org/10.5194/nhess-13-2957-2013 Lan, H. X., Martin, C. D., Zhou, C. H., 2008. Estimating the Size and Travel Distance of Klapperhorn Mountain Debris Flows for Risk Analysis along Railway, Canada. International Journal of Sediment Research, 23(3): 275-282. https://doi.org/10.1016/s1001-6279(08)60025-6 Lan, H. X., Martin, C. D., Zhou, C. H., et al., 2010. Rockfall Hazard Analysis Using LiDAR and Spatial Modeling. Geomorphology, 118(1-2): 213-223. https://doi.org/10.1016/j.geomorph.2010.01.002 Lan, H. X., Wu, F. Q., Zhou, C. H., et al., 2002. Analysis on Susceptibility of GIS Based Landslide Triggering Factors in Yunnan Xiaojiang Watershed. Chinese Journal of Rock Mechanics and Engineering, 21(10): 1500-1506(in Chinese with English abstract). doi: 10.3321/j.issn:1000-6915.2002.10.014 Lan, H. X., Xiao, R. H., Yan, F. Z., et al., 2016. The Geological Engineering Conditions Analysis for Sichuan-Tibet Interconnection Project. Journal of Engineering Geology, 24(Suppl.): 375-385(in Chinese with English abstract). Lan, H. X., Zhang, N., Li, L. P., et al., 2021. Risk Analysis of Major Engineering Geological Hazards for Sichuan-Tibet Railway in the Phase of Feasibility Study. Journal of Engineering Geology, 29(2): 326-341(in Chinese with English abstract). Lan, H. X., Zhou, C. H., Wang, L. J., et al., 2004. Landslide Hazard Spatial Analysis and Prediction Using GIS in the Xiaojiang Watershed, Yunnan, China. Engineering Geology, 76(1-2): 109-128. https://doi.org/10.1016/j.enggeo.2004.06.009 Li, L. P., Lan, H. X., 2015. Probabilistic Modeling of Rockfall Trajectories: A Review. Bulletin of Engineering Geology and the Environment, 74(4): 1163-1176. https://doi.org/10.1007/s10064-015-0718-9 Li, L. P., Lan, H. X., Guo, C. B., et al., 2017. A Modified Frequency Ratio Method for Landslide Susceptibility Assessment. Landslides, 14(2): 727-741. https://doi.org/10.1007/s10346-016-0771-x Li, L. P., Lan, H. X., Guo, C. B., et al., 2017. Geohazard Susceptibility Assessment along the Sichuan-Tibet Railway and Its Adjacent Area Using an Improved Frequency Ratio Method. Geoscience, 31(5): 911-929(in Chinese with English abstract). doi: 10.3969/j.issn.1000-8527.2017.05.004 Li, L. P., Lan, H. X., Strom, A., 2020. Automatic Generation of Landslide Profile for Complementing Landslide Inventory. Geomatics, Natural Hazards and Risk, 11(1): 1000-1030. https://doi.org/10.1080/19475705.2020.1766578 Li, L. P., Lan, H. X., Wu, Y. M., 2014. The Volume-to-Surface-Area Ratio Constrains the Rollover of the Power Law Distribution for Landslide Size. The European Physical Journal Plus, 129(5): 89. https://doi.org/10.1140/epjp/i2014-14089-y Li, L. P., Lan, H. X., Wu, Y. M., 2016. How Sample Size can Effect Landslide Size Distribution. Geoenvironmental Disasters, 3: 18. https://doi.org/10.1186/s40677-016-0052-y Li, Q. Q., Huang, D., Pei, S. F., et al., 2021. Using Physical Model Experiments for Hazards Assessment of Rainfall-Induced Debris Landslides. Journal of Earth Science, 32(5): 1113-1128. https://doi.org/10.1007/s12583-020-1398-3 Malamud, B. D., Turcotte, D. L., Guzzetti, F., et al., 2004. Landslide Inventories and Their Statistical Properties. Earth Surface Processes and Landforms, 29(6): 687-711. https://doi.org/10.1002/esp.1064 McDougall, S., 2017.2014 Canadian Geotechnical Colloquium: Landslide Runout Analysis—Current Practice and Challenges. Canadian Geotechnical Journal, 54(5): 605-620. https://doi.org/10.1139/cgj-2016-0104 Michelini, T., Bettella, F., D'Agostino, V., 2017. Field Investigations of the Interaction between Debris Flows and Forest Vegetation in Two Alpine Fans. Geomorphology, 279: 150-164. https://doi.org/10.1016/j.geomorph.2016.09.029 Nicoletti, P. G., Sorriso-Valvo, M., 1991. Geomorphic Controls of the Shape and Mobility of Rock Avalanches. Geological Society of America Bulletin, 103(10): 1365-1373. https://doi.org/10.1130/0016-7606(1991)1031365:gcotsa>2.3.co;2 doi: 10.1130/0016-7606(1991)1031365:gcotsa>2.3.co;2 Peng, L., Xu, S. N., Peng, J. H., 2014. Research on Development Characteristics and Size of Landslides in the Three Gorges Area. Geoscience, 28(5): 1077-1086(in Chinese with English abstract). doi: 10.3969/j.issn.1000-8527.2014.05.025 Qiu, H. J., Cui, P., Hu, S., et al., 2016. Size-Frequency Distribution of Landslides in Different Landforms on the Loess Plateau of Northern Shaanxi. Earth Science, 41(2): 343-350(in Chinese with English abstract). Qiu, H. J., Cui, P., Regmi, A. D., et al., 2018. The Effects of Slope Length and Slope Gradient on the Size Distributions of Loess Slides: Field Observations and Simulations. Geomorphology, 300: 69-76. https://doi.org/10.1016/j.geomorph.2017.10.020 Rana, K., Ozturk, U., Malik, N., 2021. Landslide Geometry Reveals Its Trigger. Geophysical Research Letters, 48(4): e2020GL090848. https://doi.org/10.1029/2020gl090848 Schaefer, L. N., Santi, P. M., Duron, T. C., 2021. Debris Flow Behavior during the September 2013 Rainstorm Event in the Colorado Front Range, USA. Landslides, 18(5): 1585-1595. https://doi.org/10.1007/s10346-020-01590-5 Schneider, D., Huggel, C., Haeberli, W., et al., 2011. Unraveling Driving Factors for Large Rock-Ice Avalanche Mobility. Earth Surface Processes and Landforms, 36(14): 1948-1966. https://doi.org/10.1002/esp.2218 Stark, C. P., Hovius, N., 2001. The Characterization of Landslide Size Distributions. Geophysical Research Letters, 28(6): 1091-1094. https://doi.org/10.1029/2000gl008527 Tang, C. X., van Westen, C. J., Tanyaş, H., et al., 2016. Analysing Post-Earthquake Landslide Activity Using Multi-Temporal Landslide Inventories near the Epicentral Area of the 2008 Wenchuan Earthquake. Natural Hazards and Earth System Sciences, 16(12): 2641-2655. https://doi.org/10.5194/nhess-16-2641-2016 Tanyaş, H. K., van Westen, C. J., Allstadt, K. E., et al., 2017. Presentation and Analysis of a Worldwide Database of Earthquake-Induced Landslide Inventories. Journal of Geophysical Research: Earth Surface, 122(10): 1991-2015. https://doi.org/10.1002/2017jf004236 Tsuchida, T., Moriwaki, T., Nakai, S., et al., 2019. Investigation and Consideration on Landslide Zoning of Multiple Slope Failures and Debris Flows of 2014 Disaster in Hiroshima, Japan. Soils and Foundations, 59(4): 1085-1102. https://doi.org/10.1016/j.sandf.2018.12.012 Varnes, D. J., 1958. Landslide Types and Processes. In: Eckel, E. B., ed., Landslides and Engineering Practice. NAS-NRC Publication 544, Washington, D. C. . Varnes, D. J., 1978. Slope Movement Types and Processes. In: Schuster, R. L., Krizek, R. J., eds., Landslides, Analysis and Control. National Academy of Sciences, Washington, D. C. . Wang, L. J., Ma, C., Miao, L., 2020. Morphological and Depositional Characteristics of Slope Debris Flow. Journal of Natural Disasters, 29(6): 98-106(in Chinese with English abstract). Wang, Y. F., Xu, Q., Cheng, Q. G., et al., 2016. Experimental Study on the Propagation and Deposit Features of Rock Avalanche along 3D Complex Topography. Chinese Journal of Rock Mechanics and Engineering, 35(9): 1776-1791(in Chinese with English abstract). Wu, Y. M., Lan, H. X., Gao, X., et al., 2014. Rainfall Threshold of Storm-Induced Landslides in Typhoon Areas: A Case Study of Fujian Province. Journal of Engineering Geology, 22(2): 255-262(in Chinese with English abstract). doi: 10.3969/j.issn.1004-9665.2014.02.015 Xing, A. G., Xu, Q., Gan, J. J., 2015. On Characteristics and Dynamic Analysis of the Niumian Valley Rock Avalanche Triggered by the 2008 Wenchuan Earthquake, Sichuan, China. Environmental Earth Sciences, 73(7): 3387-3401. https://doi.org/10.1007/s12665-014-3626-6 Xing, A. G., Xu, Q., Zhu, Y. Q., et al., 2016. The August 27, 2014, Rock Avalanche and Related Impulse Water Waves in Fuquan, Guizhou, China. Landslides, 13(2): 411-422. https://doi.org/10.1007/s10346-016-0679-5 Xing, A. G., Yuan, X. Y., Xu, Q., et al., 2017. Characteristics and Numerical Runout Modelling of a Catastrophic Rock Avalanche Triggered by the Wenchuan Earthquake in the Wenjia Valley, Mianzhu, Sichuan, China. Landslides, 14(1): 83-98. https://doi.org/10.1007/s10346-016-0707-5 Xu, C., Xu, X. W., Yao, X., et al., 2014. Three (nearly) Complete Inventories of Landslides Triggered by the May 12, 2008 Wenchuan Mw 7.9 Earthquake of China and Their Spatial Distribution Statistical Analysis. Landslides, 11(3): 441-461. https://doi.org/10.1007/s10346-013-0404-6 Xu, Q., Huang, R. Q., 1997. Power Law between Volume and Frequency of Geological Hazards. Journal of Chengdu University of Technology, 24(Suppl.): 91-96(in Chinese with English abstract). Yao, L. K., Huang, Y. D., Yang, Q. H., 2010. The Self-Organized Criticality of Landslids Triggered by Earthquake. Journal of Sichuan University (Engineering Science Edition), 42(5): 33-43(in Chinese with English abstract). Yin, Y. P., Wang, F. W., Sun, P., 2009. Landslide Hazards Triggered by the 2008 Wenchuan Earthquake, Sichuan, China. Landslides, 6(2): 139-152. https://doi.org/10.1007/s10346-009-0148-5 Yin, Y. P., Xing, A. G., Wang, G. H., et al., 2017. Experimental and Numerical Investigations of a Catastrophic Long-Runout Landslide in Zhenxiong, Yunnan, Southwestern China. Landslides, 14(2): 649-659. https://doi.org/10.1007/s10346-016-0729-z Zhan, W. W., Huang, R. Q., Pei, X. J., et al., 2017. Empirical Prediction Model for Movement Distance of Gully-Type Rock Avalanches. Journal of Engineering Geology, 25(1): 154-163(in Chinese with English abstract). Zhang, T., Yang, Z. H., Zhang, Y. S., et al., 2019. An Analysis of the Entrainment of the Xinmo High-Position Landslide in Maoxian County, Sichuan. Hydrogeology & Engineering Geology, 46(3): 138-145(in Chinese with English abstract). Zhang, Y. X., Lan, H. X., Li, L. P., et al., 2019. Combining Statistical Model and Physical Model for Refined Assessment of Geological Disaster—A Case Study of Longshan Community in Fujian Province. Journal of Engineering Geology, 27(3): 608-622. (in Chinese with English abstract). Zhao, J., Ouyang, C. J., Ni, S. D., et al., 2020. Analysis of the 2017 June Maoxian Landslide Processes with Force Histories from Seismological Inversion and Terrain Features. Geophysical Journal International, 222(3): 1965-1976. https://doi.org/10.1093/gji/ggaa269 Zhou, C., Yin, K. L., Cao, Y., et al., 2020. Landslide Susceptibility Assessment by Applying the Coupling Method of Radial Basis Neural Network and Adaboost: A Case Study from the Three Gorges Reservoir Area. Earth Science, 45(6): 1865-1876(in Chinese with English abstract). Zhou, L., Fan, X. M., Xu, Q., et al., 2019. Numerical Simulation and Hazard Prediction on Movement Process Characteristics of Baige Landslide in Jinsha River. Journal of Engineering Geology, 27(6): 1395-1404(in Chinese with English abstract). Zhou, S. H., Fang, L. G., Liu, B. C., 2015. Slope Unit-Based Distribution Analysis of Landslides Triggered by the April 20, 2013, Ms 7.0 Lushan Earthquake. Arabian Journal of Geosciences, 8(10): 7855-7868. https://doi.org/10.1007/s12517-015-1835-2 Zhuang, J. Q., Cui, P., Hu, K. H., et al., 2010. Characteristics of Earthquake-Triggered Landslides and Post-Earthquake Debris Flows in Beichuan County. Journal of Mountain Science, 7(3): 246-254. https://doi.org/10.1007/s11629-010-2016-0 柴波, 陶阳阳, 杜娟, 等, 2020. 西藏聂拉木县嘉龙湖冰湖溃决型泥石流危险性评价. 地球科学, 45(12): 4630-4639. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202012024.htm 杜娟, 殷坤龙, 王佳佳, 2015. 基于有限体积法的滑坡-碎屑流三维运动过程模拟分析. 岩石力学与工程学报, 34(3): 480-488. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201503006.htm 樊晓一, 张睿骁, 胡晓波, 2020. 沟谷地形参数对滑坡运动距离的影响研究. 地质力学学报, 26(1): 106-114. 胡瑞林, 范林峰, 王珊珊, 等, 2013. 滑坡风险评价的理论与方法研究. 工程地质学报, 21(1): 76-84. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201301013.htm 胡晓波, 樊晓一, 马新, 2019. 高速远程滑坡加速运动过程能量消耗评判研究. 人民长江, 50(2): 191-196. https://www.cnki.com.cn/Article/CJFDTOTAL-RIVE201902034.htm 胡元鑫, 刘新荣, 蒋洋, 等, 2011. 非完整滑坡编目三参数反Gamma概率分布模型. 中南大学学报(自然科学版), 42(10): 3176-3181. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201110048.htm 兰恒星, 伍法权, 周成虎, 等, 2002. 基于GIS的云南小江流域滑坡因子敏感性分析. 岩石力学与工程学报, 21(10): 1500-1506. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200210015.htm 兰恒星, 肖锐铧, 严福章, 等, 2016. 川藏联网工程地质条件分析. 工程地质学报, 24(增刊): 375-385. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-GCDZ201610001057.htm 兰恒星, 张宁, 李郎平, 等, 2021. 川藏铁路可研阶段重大工程地质风险分析. 工程地质学报, 29(2): 326-341. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202102004.htm 李郎平, 兰恒星, 郭长宝, 等, 2017. 基于改进频率比法的川藏铁路沿线及邻区地质灾害易发性分区评价. 现代地质, 31(5): 911-929. https://www.cnki.com.cn/Article/CJFDTOTAL-XDDZ201705004.htm 彭令, 徐素宁, 彭军还, 2014. 三峡库区滑坡规模与发育特征研究. 现代地质, 28(5): 1077-1086. https://www.cnki.com.cn/Article/CJFDTOTAL-XDDZ201405026.htm 邱海军, 崔鹏, 胡胜, 等, 2016. 陕北黄土高原不同地貌类型区黄土滑坡频率分布. 地球科学, 41(2): 343-350. doi: 10.3799/dqkx.2016.026 王丽娟, 马超, 苗绿, 2020. 坡面泥石流形态和堆积特征研究. 自然灾害学报, 29(6): 98-106. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH202006010.htm 王玉峰, 许强, 程谦恭, 等, 2016. 复杂三维地形条件下滑坡-碎屑流运动与堆积特征物理模拟实验研究. 岩石力学与工程学报, 35(9): 1776-1791. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201609007.htm 伍宇明, 兰恒星, 高星, 等, 2014. 台风暴雨型滑坡降雨阈值曲线研究——以福建地区为例. 工程地质学报, 22(2): 255-262. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201402014.htm 许强, 黄润秋, 1997. 地质灾害发生频率的幂律规则. 成都理工大学学报(自然科学版), 24(增刊): 91-96. https://www.cnki.com.cn/Article/CJFDTOTAL-CDLG7S1.013.htm 姚令侃, 黄艺丹, 杨庆华, 2010. 地震触发崩塌滑坡自组织临界性研究. 四川大学学报(工程科学版), 42(5): 33-43. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201005007.htm 詹威威, 黄润秋, 裴向军, 等, 2017. 沟道型滑坡-碎屑流运动距离经验预测模型研究. 工程地质学报, 25(1): 154-163. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201701021.htm 张涛, 杨志华, 张永双, 等, 2019. 四川茂县新磨村高位滑坡铲刮作用分析. 水文地质工程地质, 46(3): 138-145. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201903019.htm 仉义星, 兰恒星, 李郎平, 等, 2019. 综合统计模型和物理模型的地质灾害精细评估——以福建省龙山社区为例. 工程地质学报, 27(3): 608-622. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201903020.htm 周超, 殷坤龙, 曹颖, 等, 2020. 基于集成学习与径向基神经网络耦合模型的三峡库区滑坡易发性评价. 地球科学, 45(6): 1865-1876. doi: 10.3799/dqkx.2020.071 周礼, 范宣梅, 许强, 等, 2019. 金沙江白格滑坡运动过程特征数值模拟与危险性预测研究. 工程地质学报, 27(6): 1395-1404. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201906022.htm 期刊类型引用(9)
1. 房颖晖,李郎平,杨文涛,兰恒星,田静,高佳鑫. 利用形变时序分形特征识别高山冰川区滑坡. 地球信息科学学报. 2025(01): 239-255 .  百度学术
百度学术2. 杨锟,叶永,谢旋. 基于离散元模型的聚合型滑坡碎屑流聚合角度影响研究. 地质科技通报. 2025(02): 116-129 .  百度学术
百度学术3. 佟彬,殷跃平,李昺,唐继婷,杨旭东,徐子烜. 地质灾害人工智能大语言模型研究展望. 中国地质灾害与防治学报. 2025(02): 1-12 .  百度学术
百度学术4. 谢强,陈昱成,田仁珺,傅翔,班宇鑫. 复杂运动路径下滑坡转向变形机理研究. 地下空间与工程学报. 2024(02): 615-624+635 .  百度学术
百度学术5. 史安文,程谦恭,王玉峰,林棋文,明杰. 高速远程滑坡流态化地貌研究综述. 工程地质学报. 2024(03): 978-995 .  百度学术
百度学术6. 田仁珺. 基于PFC3D的庞家湾滑坡运动过程模拟研究. 江西建材. 2024(06): 205-209 .  百度学术
百度学术7. 周健,刘港. 基于模糊综合评价法的凤鸣镇滑坡危险性评价. 科学咨询(科技·管理). 2022(05): 113-116 .  百度学术
百度学术8. 蔡浩杰,韩海辉,张雨莲,王立社. 基于地形特征融合的卷积神经网络滑坡识别. 地球科学与环境学报. 2022(03): 568-579 .  百度学术
百度学术9. 刘世杰,兰恒星,包含,彭建兵. 石窟寺典型工程地质变形破坏模式及分类体系. 地球科学. 2022(12): 4710-4723 .  本站查看
本站查看其他类型引用(6)
-










 下载:
下载:










 下载:
下载:



 百度学术
百度学术












