Inverse Modeling of Parameterized Hydraulic Conductivity Field in a Fractured Medium Based on Pilot Point Method
-
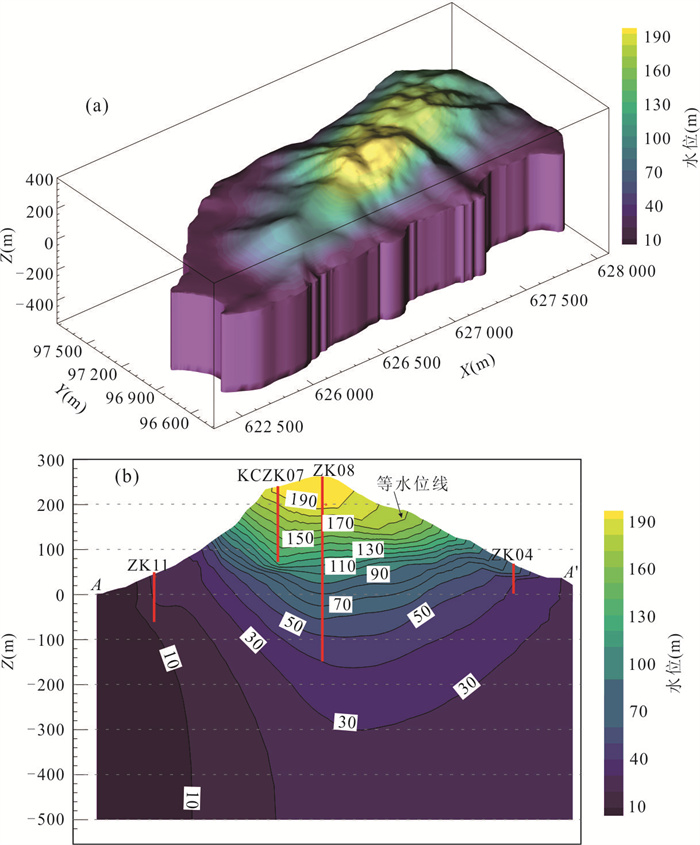
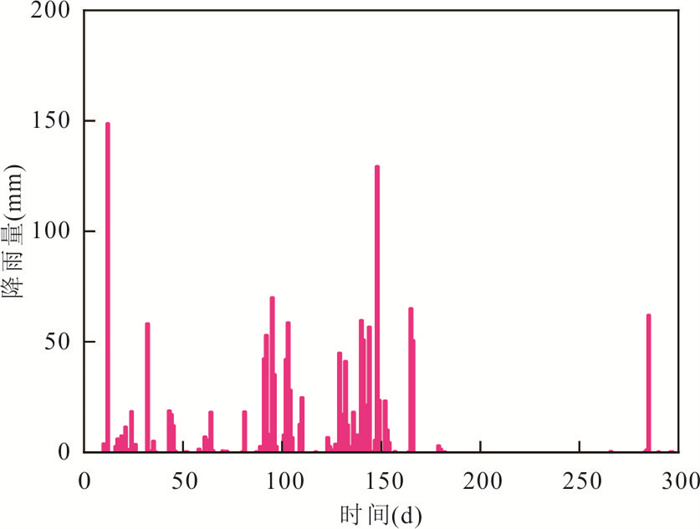
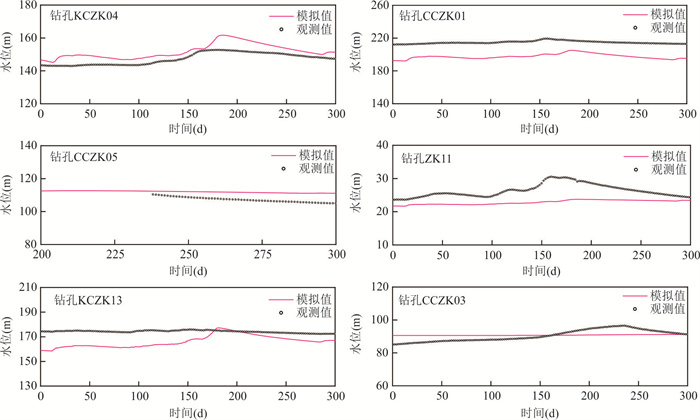
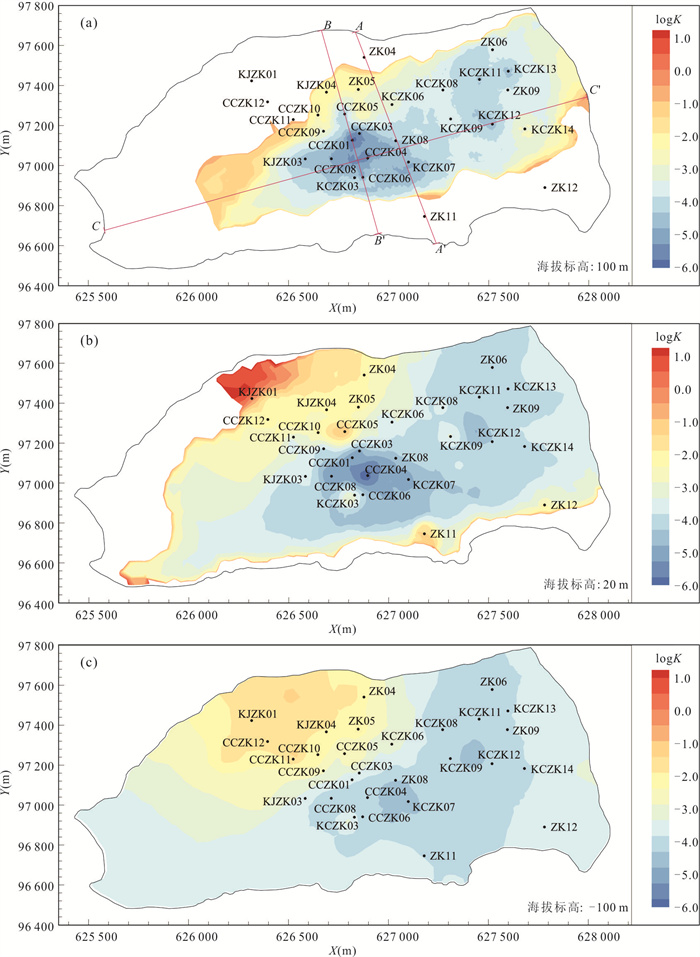
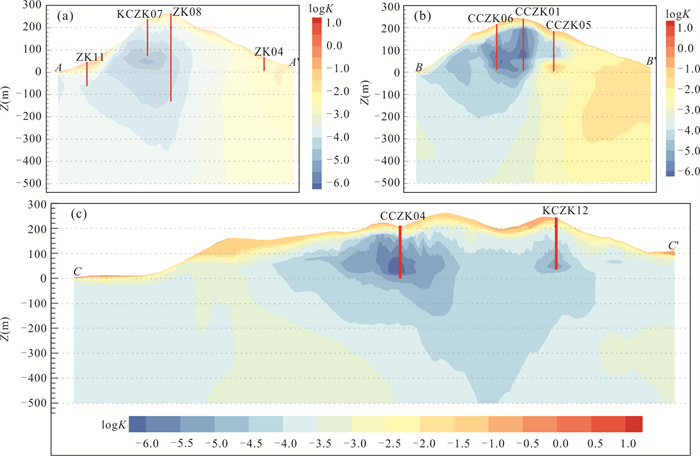
摘要: 在裂隙岩体地下工程中，渗透性能是工程场地水文地质条件最为关注的关键因素之一，对工程场地最终安全性能评价起着至关重要的作用.以我国沿海某核设施花岗岩场地为研究对象，采用Pilot Point调参方法、PEST并行反演程序及3D克里金插值方式，表征裂隙岩体的渗透空间结构.研究表明：该方法可较好地拟合稳定条件下钻孔水位，验证地下水位动态演化趋势；建立的参数化渗透结构模型在实测数据分布的区域反演结果更为精细，模型参数的综合灵敏度程度受观测水位的位置、数量及变程等影响.Pilot Point方法一定程度上可以识别裂隙介质渗透结构的空间差异性，有助于进一步提升裂隙介质渗流模拟预测能力.Abstract: For the underground engineering site in a fractured rock mass, the hydraulic conductivity is a critical factor influencing hydrogeological conditions and plays a pivotal role in the final assessment of site performance. This study focuses on the granite formation of nuclear facility site in the coastal area, China. It applied the Pilot Point calibration technique in conjunction with a 3D kriging interpolation method to establish a parameterized hydraulic conductivity field for the fractured medium. Besides, the inverse parameter estimation tool PEST for automated calibration and sensitivity analysis was employed. The results indicate that the simulated hydraulic heads were in a good agreement with the measured data in the steady condition, and well reproduced dynamic behavior of groundwater level with time. Notably, the hydraulic conductivity filed could be estimated more accurately around the boreholes and the parameter sensitivity was related with borehole location, borehole quantity and variogram range. Based on these findings, it could conclude that Pilot Point method could identify spatial difference of hydraulic conductivity filed in the fractured rocks. It is positive to further improve the groundwater flow prediction ability in the fracture medium.
-
图 3 PEST程序参数识别流程图与相应原理方程编号
Fig. 3. Diagram of the PEST code workflow and the number points to the equation of the corresponding step
图 4 钻孔ZK11中地下水电导率与TDS的监测结果
Fig. 4. Recorded data for conductivity and TDS in borehole ZK11
图 6 研究区渗透参数垂向方向（a）和水平NE45°方向（b）实验变异函数拟合曲线
Fig. 6. Semi-variogram and correlation length of log-transformed K data along the vertical direction (a) and the NE45° direction (b) in the study area
图 7 Pilot Point调参点空间分布(a)和平面布设与参数分区(b)
Fig. 7. Pilot Point locations in the numerical model (a) and planar graphs of Pilot Point locations and parameter zones (b)
图 9 钻孔CCZK05分层监测水位埋深结果
Fig. 9. Recorded data of groundwater depth from borehole CCZK05 utilizing the multi-layer monitoring system
图 10 稳定条件下的钻孔观测水位与模拟水位对比
Fig. 10. Comparison of the numerical and recorded hydraulic head of different boreholes in the steady-state condition
图 11 研究区地下水位稳定流模拟结果
Fig. 11. Groundwater level distribution in the steady-state condition
图 13 不同钻孔模拟水位与观测水位随时间对比
Fig. 13. Comparison of the numerical and recorded hydraulic head with time in different boreholes
图 15 不同剖面图的渗透系数模拟结果
Fig. 15. Hydraulic conductivity distribution of different profiles
图 16 模型中PilotPoint参数点的反演结果
Fig. 16. Numerical results of hydraulic conductivity of Pilot Points in the model
图 17 模型中各个参数分区的综合灵敏度分析结果
Fig. 17. Comprehensive sensitivities for hydrogeological zones in the model
图 18 PilotPoint点渗透系数的综合灵敏度分析结果
Fig. 18. Comprehensive sensitivities for hydraulic conductivity of Pilot Points in the model
图 19 观测水位对微风化层渗透结构灵敏度分析结果
Fig. 19. Sensitivities of different boreholes for hydraulic conductivity field in weakly weathered granite zone
表 1 van Genuchten-Mualem模型经验参数
Table 1. Empirical parameters of van Genuchten-Mualem model
岩性 残余含水率θr 饱和含水率θs 经验参数
α（cm-1）经验参数n 砂土 0.065 0.410 0.075 000 1.89 粉质粘土 0.131 0.396 0.004 230 2.06 花岗岩 0.000 0.008 0.000 064 1.34 
下载: 导出CSV
表 2 模型不同岩性净入渗量反演结果(m/d)
Table 2. Numerical results of net infiltration mass for hydrogeological zones in the model (unit: m/d)
岩性 最小值 最大值 初始值 反演结果 中细粒花岗岩 1.0×10-8 9.65×10-5 1.0×10-5 1.21×10-4 斑状花岗岩 1.0×10-8 9.65×10-5 1.0×10-5 7.69×10-4 花岗斑岩 1.0×10-8 9.65×10-5 1.0×10-5 5.67×10-4 二长花岗岩 1.0×10-8 9.65×10-5 1.0×10-5 2.87×10-7 海相砂层 1.0×10-8 9.65×10-5 1.0×10-5 4.80×10-6 人工堆积层 1.0×10-8 9.65×10-5 1.0×10-5 7.41×10-8
下载: 导出CSV
表 3 模型参数分区渗透系数的反演结果(m/d)
Table 3. Numerical results of hydraulic conductivity for hydrogeological zones in the model (unit: m/d)
岩性 最小值 最大值 初始值 反演结果 全风化层 中细粒花岗岩 0.1 5.0 0.1 0.500 斑状花岗岩 0.1 5.0 0.1 0.116 花岗斑岩 0.1 5.0 0.1 0.100 二长花岗岩 0.1 5.0 0.1 0.132 强风化层 中细粒花岗岩 0.05 0.5 0.1 0.100 斑状花岗岩 0.05 0.5 0.1 0.061 花岗斑岩 0.05 0.5 0.1 0.056 二长花岗岩 0.05 0.5 0.1 0.077 中风化层 中细粒花岗岩 0.001 0.1 0.01 0.003 斑状花岗岩 0.001 0.1 0.01 0.001 花岗斑岩 0.001 0.1 0.01 0.024 二长花岗岩 0.001 0.1 0.01 0.006 第四系 海相砂层 10.0 25.0 15.0 11.170 人工堆积层 1.0 20.0 10.0 5.162
下载: 导出CSV
-
Anderson, M. P., Woessner, W. W., Hunt, R. J., 2015. Applied Groundwater Modeling: Simulation of Flow and Advective Transport. Academic Press, San Diego. Blessent, D., Therrien, R., Lemieux, J. M., 2011. Inverse Modeling of Hydraulic Tests in Fractured Crystalline Rock Based on a Transition Probability Geostatistical Approach. Water Resources Research, 47(12): W12530. https://doi.org/10.1029/2011wr011037 Carle, S. F., Fogg, G. E., 1996. Transition Probability-Based Indicator Geostatistics. Mathematical Geology, 28(4): 453-476. https://doi.org/10.1007/BF02083656 Carniato, L., Schoups, G., Giesen, N., et al., 2015. Highly Parameterized Inversion of Groundwater Reactive Transport for a Complex Field Site. Journal of Contaminant Hydrology, 173: 38-58. https://doi.org/10.1016/j.jconhyd.2014.12.001 Chen, Y. F., Ling, X. M., Liu, M. M., et al., 2018. Statistical Distribution of Hydraulic Conductivity of Rocks in Deep-Incised Valleys, Southwest China. Journal of Hydrology, 566: 216-226. https://doi.org/10.1016/j.jhydrol.2018.09.016 China Geological Survey, 2012. Hydrogeological Manual (2nd Edition). Geological Publishing House, Beijing, 680-684 (in Chinese). Clifton, P. M., Neuman, S. P., 1982. Effects of Kriging and Inverse Modeling on Conditional Simulation of the Avra Valley Aquifer in Southern Arizona. Water Resources Research, 18(4): 1215-1234. https://doi.org/10.1029/wr018i004p01215 De Marsily, G., Lavedan, G., Boucher, M., et al., 1984. Interpretation of Interference Tests in a Well Field Using Geostatistical Techniques to Fit the Permeability Distribution in a Reservoir Model. Geostatistics for Natural Resources Characterization. Springer Netherlands, Dordrecht, 831-849. https://doi.org/10.1007/978-94-009-3701-7_16 Deutsch, C. V., Journel, A. G., 1998. GSLIB: Geostatistical Software and User's Guide (Second Edition). Oxford University Press, New York. Doherty, J., 2015. Calibration and Uncertainty Analysis for Complex Environmental Models. Watermark Numerical Computing, Brisbane, Australia. El Idrysy, E. H., Smedt, F., 2007. A Comparative Study of Hydraulic Conductivity Estimations Using Geostatistics. Hydrogeology Journal, 15(3): 459-470. https://doi.org/10.1007/s10040-007-0166-0 Fang, K., Ji, X., Shen, C., et al., 2019. Combining a Land Surface Model with Groundwater Model Calibration to Assess the Impacts of Groundwater Pumping in a Mountainous Desert Basin. Advances in Water Resources, 130: 12-28. https://doi.org/10.1016/j.advwatres.2019.05.008 Finsterle, S., 2006. Demonstration of Optimization Techniques for Groundwater Plume Remediation Using iTOUGH2. Environmental Modelling & Software, 21(5): 665-680. https://doi.org/10.1016/j.envsoft.2004.11.012 Follin, S., Hartley, L., Rhén, I., et al., 2014. A Methodology to Constrain the Parameters of a Hydrogeological Discrete Fracture Network Model for Sparsely Fractured Crystalline Rock, Exemplified by Data from the Proposed High-Level Nuclear Waste Repository Site at Forsmark, Sweden. Hydrogeology Journal, 22(2): 313-331. https://doi.org/10.1007/s10040-013-1080-2 Gu, W. Z., Pang, Z. H., Wang, Q. J., et al., 2011. Isotope Hydrology. Science Press, Beijing, 432(in Chinese). Guo, Y. H., Wang, J., Jin, Y. X., 2001. The General Situation of Geological Disposal Repository Siting in the World and Research Progress in China. Earth Science Frontiers, 8(2): 327-332(in Chinese with English abstract). doi: 10.3321/j.issn:1005-2321.2001.02.017 Hartley, L., Joyce, S., 2013. Approaches and Algorithms for Groundwater Flow Modeling in Support of Site Investigations and Safety Assessment of the Forsmark Site, Sweden. Journal of Hydrology, 500: 200-216. https://doi.org/10.1016/j.jhydrol.2013.07.031 Huo, S. Y., Jin, M. G., 2017. Effect of Parameter Sensitivity of van Genuchten Model on Numerical Simulation of Rainfall Recharge. Earth Science, 42(3): 447-452 (in Chinese with English abstract). Jiang, L. Q., Sun, R. L., Liang, X., 2021. Predicting Groundwater Flow and Transport in the Heterogeneous Aquifer Sandbox Using Different Parameter Estimation Methods. Earth Science, 46(11): 4150-4160 (in Chinese with English abstract). Kapoor, A., Kashyap, D., 2021. Parameterization of Pilot Point Methodology for Supplementing Sparse Transmissivity Data. Water, 13(15): 2082. https://doi.org/10.3390/w13152082 Keller, J., Franssen, H., Nowak, W., 2021. Investigating the Pilot Point Ensemble Kalman Filter for Geostatistical Inversion and Data Assimilation. Advances in Water Resources, 155: 104010. https://doi.org/10.1016/j.advwatres.2021.104010 Li, Y. G., Lan, J. K., Li, R. L., et al., 2016. Permeability Coefficients of Weathering Zones in Huashan Granite of Guangxi. Journal of Guilin University of Technology, 36(4): 681-687(in Chinese with English abstract). doi: 10.3969/j.issn.1674-9057.2016.04.006 Maji, R., Sudicky, E. A., Panday, S., et al., 2006. Transition Probability/Markov Chain Analyses of DNAPL Source Zones and Plumes. Ground Water, 44(6): 853-863. https://doi.org/10.1111/j.1745-6584.2005.00194.x Park, Y. J., Sudicky, E. A., McLaren, R. G., et al., 2004. Analysis of Hydraulic and Tracer Response Tests within Moderately Fractured Rock Based on a Transition Probability Geostatistical Approach. Water Resources Research, 40(12): W12404. https://doi.org/10.1029/2004wr003188 Poeter, E. P., Hill, M. C., 1999. UCODE, a Computer Code for Universal Inverse Modeling. Computers & Geosciences, 25(4): 457-462. https://doi.org/10.1016/s0098-3004(98)00149-6 Rubin, Y., Gómez-Hernández, J. J., 1990. A Stochastic Approach to the Problem of Upscaling of Conductivity in Disordered Media: Theory and Unconditional Numerical Simulations. Water Resources Research, 26(4): 691-701. https://doi.org/10.1029/wr026i004p00691 Sivakumar, B., Halter, T., Zhang, H., 2005. A Fractal Investigation of Solute Travel Time in a Heterogeneous Aquifer: Transition Probability/Markov Chain Representation. Ecological Modelling, 182(3/4): 355-370. https://doi.org/10.1016/j.ecolmodel.2004.04.010 Usman, M., Qamar, M. U., Becker R., et al., 2020. Numerical Modelling and Remote Sensing Based Approaches for Investigating Groundwater Dynamics under Changing Land-Use and Climate in the Agricultural Region of Pakistan. Journal of Hydrology, 581: 124408. https://doi.org/10.1016/j.jhydrol.2019.124408 van Genuchten, M. T., 1980. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44(5): 892-898. https://doi.org/10.2136/sssaj1980.03615995004400050002x Wang, J. Zhang, T. L., Zheng, H. L., 1999. Geological Disposal of Radioactive Waste in the World. Atomic Energy Press, Beijing(in Chinese). Wen, X. H., Capilla, J. E., Deutsch, C. V., et al., 1999. A Program to Create Permeability Fields That Honor Single-Phase Flow Rate and Pressure Data. Computers & Geosciences, 25(3): 217-230. https://doi.org/10.1016/S0098-3004(98)00126-5 Xue, Y. Q., 1986. Principles of Groundwater Dynamics. Geological Publishing House, Beijing (in Chinese). Yang, J. Z., Cai, S. Y., Huang, G. H., et al., 2000. Stochastic Theory of Groundwater and Solute Transport in Porous Media. Science Press, Beijing, 21-48 (in Chinese). Yeh, T. C., Liu, S. Y., 2000. Hydraulic Tomography: Development of a New Aquifer Test Method. Water Resources Research, 36(8): 2095-2105. https://doi.org/10.1029/2000WR900114 Zhang, H., Harter, T., Sivakumar, B., 2006. Nonpoint Source Solute Transport Normal to Aquifer Bedding in Heterogeneous, Markov Chain Random Fields. Water Resources Research, 42(6): W06403. https://doi.org /10.1029/2004WR003808 Zhao, P., Liu, J., Chen, L., et al., 2017. Experimental Study on Gas Relative Permeability of Unsaturated Granite. Chinese Journal of Underground Space and Engineering, 13(1): 57-62, 70(in Chinese with English abstract). Zhou, H. Y., 2011. Parameter Identification of Non-Gaussian Aquifer Based on Ensemble Kalman Filter Method (Dissertation). China University of Geosciences, Beijing (in Chinese with English abstract). 顾慰祖, 庞忠和, 王全九, 等, 2011. 同位素水文学. 北京: 科学出版社, 432. 郭永海, 王驹, 金远新, 2001. 世界高放废物地质处置库选址研究概况及国内进展. 地学前缘, 8(2): 327-332. doi: 10.3321/j.issn:1005-2321.2001.02.017 霍思远, 靳孟贵, 2017. Van Genuchten模型参数对降水入渗数值模拟的敏感性. 地球科学, 42(3): 447-452. https://www.cnki.com.cn/Article/CJFDTOTAL-JDXG201707008.htm 蒋立群, 孙蓉琳, 梁杏. 2021. 含水层非均质性不同刻画方法对地下水流和溶质运移预测的影响. 地球科学, 46(11): 4150-4160. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202111027.htm 李有光, 蓝俊康, 黎容伶, 等, 2016. 广西花山花岗岩体风化带的渗透系数. 桂林理工大学学报, 36(4): 681-687. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGX201604006.htm 王驹, 张铁岭, 郑华铃, 1999. 世界放射性废物地质处置. 北京: 原子能出版社. 薛禹群, 1986. 地下水动力学原理. 北京: 地质出版社. 杨金忠, 蔡树英, 黄冠华, 等, 2000. 多孔介质中水分及溶质运移的随机理论. 北京: 科学出版社, 21-48. 赵鹏, 刘健, 陈亮, 等, 2017. 非饱和花岗岩气体相对渗透率试验研究. 地下空间与工程学报, 13(1): 57-62, 70. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201701009.htm 中国地质调查局, 2012. 水文地质手册. 第2版. 北京: 地质出版社, 680-684. 周海燕, 2011. 基于集合卡尔曼滤波法的非高斯含水层参数识别（博士学位论文）. 北京:中国地质大学 . -
点击查看大图
计量
- 文章访问数: 278
- HTML全文浏览量: 467
- PDF下载量: 26
- 被引次数: 0
