Effect of Stress Loading on Permeability of Granite Rough Fissure
-
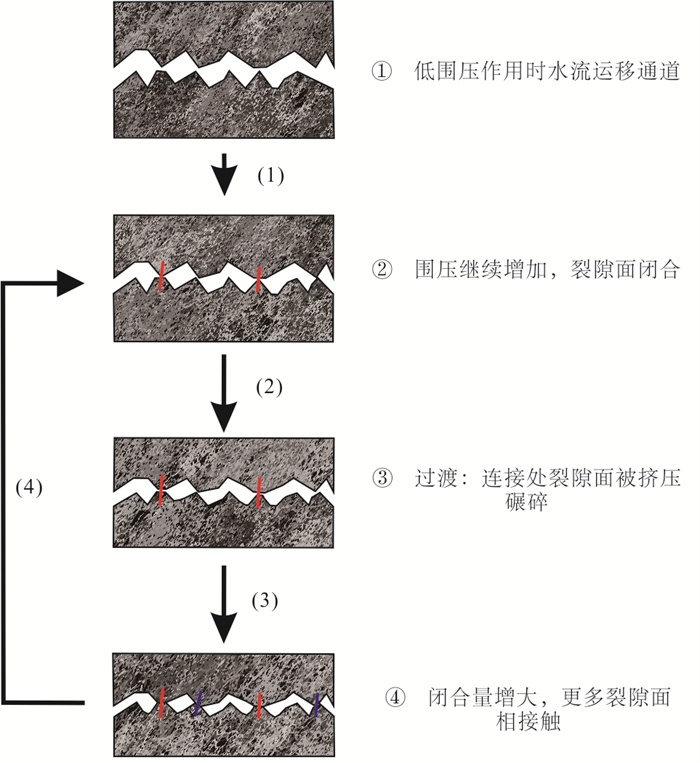
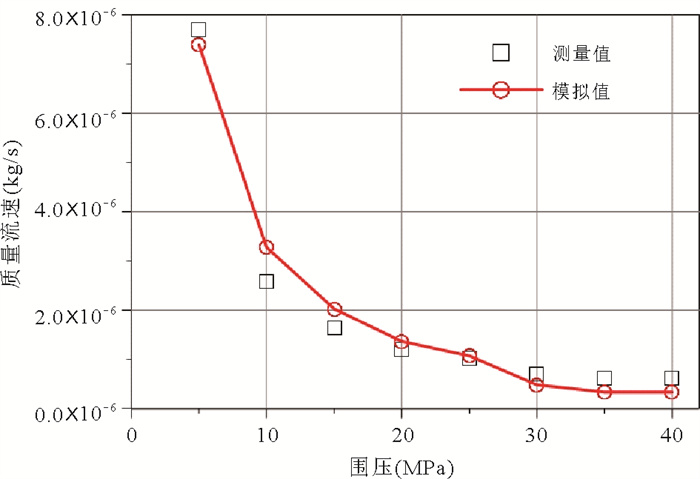
摘要: 本研究选取青海共和盆地干热岩靶区储热层印支期花岗岩为目标层，利用高压流体驱替实验装置开展岩心裂隙渗流-应力耦合下循环加卸载试验，分析应力加载过程对花岗岩粗糙裂隙渗透率影响规律，并通过数值模拟技术分析实验过程中花岗岩裂隙渗透率的演化特征.研究结果表明：（1）应力加载导致裂隙接触面产生变形，是影响裂隙渗流的主要因素，裂隙渗透率与围压呈负相关关系；（2）裂隙渗透率对不同应力加载模式敏感性存在差异；（3）在试验基础上得出数学经验公式，并通过数值模拟分析花岗岩裂隙通道内渗流演化规律，模拟结果同实验拟合较好.Abstract: Selecting Indosinian granite in thermal storage layer of hot dry rock targets in the Gonghe basin, Qinghai Province, as the goal layer, using high pressure fluid displacement experiment device, the core fissure seepage and stress coupling loops and unloading test was carried out in this study. The influence law of stress loading process on granite rough fracture permeability was analyzed, and the evolution characteristics of granite fracture permeability in the experimental process were analyzed by numerical simulation technology. The results show that: (1) stress loading leads to deformation of fracture contact surface, which is the main factor affecting fracture seepage, and fracture permeability is negatively correlated with confining pressure. (2) The sensitivity of fracture permeability to different stress loading modes is different; (3) The mathematical empirical formula is obtained on the basis of the test, and the seepage evolution law in the granite fracture channel is analyzed by numerical simulation. The simulation results fit well with the experiment.
-
图 2 高温高压孔隙流体驱替试验系统示意
Fig. 2. Schematic diagram of high temperature and high pressure pore fluid displacement test system
图 3 一次循环加、卸载条件下花岗岩裂隙渗透率变化曲线
Fig. 3. Variation curve of granite fracture permeability under cyclic loading and unloading conditions
图 4 试样Y-1三次循环加卸载渗透率变化曲线
Fig. 4. Permeability curve of sample Y-1 after three cycles of loading and unloading
图 5 粗糙裂隙表面变形过程示意
Fig. 5. Schematic diagram of surface deformation process of rough crack
图 6 裂隙渗透率与围压关系拟合曲线
Fig. 6. Fitting curve of fracture permeability and confining pressure
图 7 花岗岩粗糙裂隙流‒固耦合试验概念模型
Fig. 7. Conceptual model of fluid-solid coupling test in granite rough fissure
图 8 花岗岩粗糙裂隙流‒固耦合试验模型数值剖分
Fig. 8. Numerical division of the fluid-solid coupling test model for granite rough fractures
图 9 不同围压条件下实验测定和模拟预测质量流速结果对比
Fig. 9. Comparison of experimental and simulated predicted mass flow rates under different confining pressures
表 1 花岗岩粗糙单裂隙渗流‒应力耦合实验方案
Table 1. Experimental scheme of seepage and stress coupling in rough single fracture of granite
试样编号 渗透压力(MPa) 初始围压(MPa) 最高围压(MPa) 间隔值(MPa) 循环次数 Y-1 3 5 40 5 3 Y-2 3 5 40 5 1 
下载: 导出CSV
表 2 加、卸载条件下花岗岩裂隙渗透率测试结果
Table 2. Test results of granite fracture permeability under loading and unloading conditions
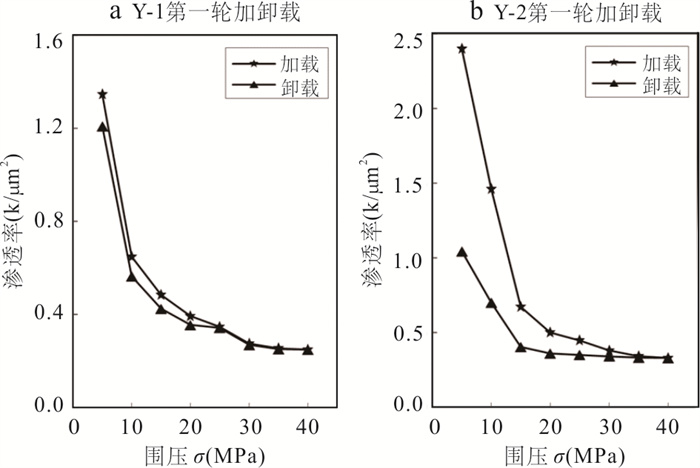
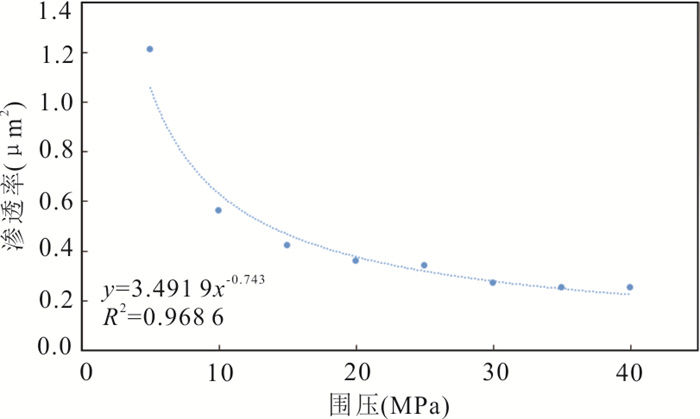
围压(MPa) Y-1 Y-2 加载k(m2) 卸载k(m2) ∆k(m2) 加载k(m2) 卸载k(m2) ∆k(m2) 5 1.35 1.21 0.14 2.40 1.04 1.35 10 0.65 0.56 0.08 1.46 0.70 0.76 15 0.48 0.42 0.06 0.67 0.40 0.27 20 0.39 0.36 0.04 0.50 0.36 0.14 25 0.35 0.34 0.01 0.45 0.35 0.10 30 0.27 0.27 0.01 0.38 0.34 0.04 35 0.25 0.25 0.00 0.34 0.33 0.01 40 0.25 0.25 0.00 0.33 0.33 0.00
下载: 导出CSV
表 3 Y-1试样3次循环加卸载试验后渗透率变化量
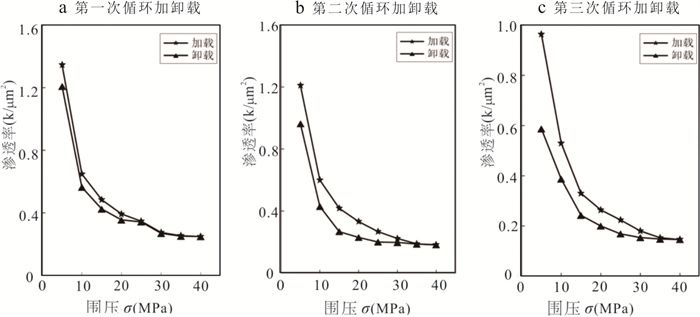
Table 3. Permeability changes of SAMPLE Y-1 after three cycles of loading and unloading tests
循环次数 加载k 卸载k(μm2) ∆k(μm2) 1 1.35 1.21 0.14 2 1.21 0.96 0.25 3 0.96 0.59 0.37
下载: 导出CSV
表 4 三维TOUGH2Biot水热过程控制方程
Table 4. Governing equations of fluid and heat flow in 3D TOUGH2Biot
描述 主要控制方程 多相流动过程(H) $ \frac{\mathrm{d}}{\mathrm{d}t}\underset{{V}_{n}}{\int }{M}^{\kappa }\mathrm{d}V=\underset{{\mathit\Gamma }_{n}}{\int }{F}^{\kappa }•n\mathrm{d}\mathit\Gamma +\underset{{V}_{n}}{\int }{q}^{\kappa }\mathrm{d}V $，
左边：$ {M}^{\kappa }=\sum\limits _{\beta =\mathrm{A}, \mathrm{G}}\varphi {S}_{\beta }{\rho }_{\beta }{X}_{\beta }^{\kappa }, \kappa =\mathrm{w}, \mathrm{i}, \mathrm{g} $，
右边：$ {\mathit{F}}_{\beta }^{\kappa }=-k\frac{{k}_{\mathrm{r}\beta }{\rho }_{\mathrm{A}}}{{\mu }_{\beta }}{X}_{\beta }^{\kappa }(\nabla {P}_{\beta }-{\rho }_{\beta }g)+{J}_{\beta }^{\kappa }, \kappa =w, i, g $，热对流传导过程(T) $ \frac{\mathrm{d}}{\mathrm{d}t}\underset{{V}_{n}}{\int }{M}^{\kappa +1}\mathrm{d}V=\underset{{\mathit\Gamma }_{n}}{\int }{F}^{\kappa +1}•n\mathrm{d}\mathit\Gamma +\underset{{V}_{n}}{\int }{q}^{\kappa +1}\mathrm{d}V $，
左边：$ {M}^{\kappa +1}=(1-\varphi){\rho }_{\mathrm{R}}{C}_{\mathrm{R}}T+\sum\limits _{\beta =\mathrm{A}, \mathrm{G}}\varphi {S}_{\beta }{\rho }_{\beta }{u}_{\beta } $，
右边：$ {F}_{}^{\kappa +1}=-\lambda \nabla T+\sum\limits _{\beta }{h}_{\beta }{F}_{\beta } $.注：式中：M为单位体积的质量或能量；t为时间；F为质量或能量通量；Vn为第n个单元的体积；$ {\mathit\Gamma }_{n} $为第n个单元的边界；q为源汇项；$ \phi $为孔隙度；S为饱和度；ρ为密度；X为质量分数；k为渗透率；kr为相对渗透率；μ为黏度；P为压力；g为重力加速度；D为弥散项；ρR为岩石颗粒密度；CR为岩石颗粒比热容；T为温度；u为内能；λ为热传导系数；h为热焓；β=A，G为液相和气相；κ=w, i, g为水、盐和气体；κ+1表示热.
下载: 导出CSV
表 5 三维TOUGH2Biot力学模拟拓展
Table 5. 3D TOUGH2Biot mechanical simulation expansion
位移 $ \left.\begin{array}{l}-G{\nabla }^{2}{w}_{x}-\frac{G}{1-2\upsilon }\frac{\partial }{\partial x}(\frac{\partial {w}_{x}}{\partial x}+\frac{\partial {w}_{y}}{\partial y}+\frac{\partial {w}_{z}}{\partial z})+\frac{\partial P}{\partial x}+3\beta K\frac{\partial T}{\partial x}=0, \\ -G{\nabla }^{2}{w}_{y}-\frac{G}{1-2\upsilon }\frac{\partial }{\partial y}(\frac{\partial {w}_{x}}{\partial x}+\frac{\partial {w}_{y}}{\partial y}+\frac{\partial {w}_{z}}{\partial z})+\frac{\partial P}{\partial y}+3\beta K\frac{\partial T}{\partial y}=0, \\ -G{\nabla }^{2}{w}_{z}-\frac{G}{1-2\upsilon }\frac{\partial }{\partial z}(\frac{\partial {w}_{x}}{\partial x}+\frac{\partial {w}_{y}}{\partial y}+\frac{\partial {w}_{z}}{\partial z})+\frac{\partial P}{\partial z}+3\beta K\frac{\partial T}{\partial z}=\gamma .\end{array}\right\} $ 应力应变 $ \left.\begin{array}{l}{\sigma }_{x}^{\mathrm{\text{'}}}={\sigma }_{x}-P=2G(\frac{\upsilon }{1-2\upsilon }{\epsilon }_{v}+{\epsilon }_{x})+3{\beta }_{T}KT, \\ {\sigma }_{y}^{\mathrm{\text{'}}}={\sigma }_{y}-P=2G(\frac{\upsilon }{1-2\upsilon }{\epsilon }_{v}+{\epsilon }_{y})+3{\beta }_{T}KT, \\ {\sigma }_{z}^{\mathrm{\text{'}}}={\sigma }_{z}-P=2G(\frac{\upsilon }{1-2\upsilon }{\epsilon }_{v}+{\epsilon }_{z})+3{\beta }_{T}KT, \\ {\tau }_{yz}^{}=G{\gamma }_{yz}, {\tau }_{zx}^{}=G{\gamma }_{zx}, {\tau }_{xy}^{}=G{\gamma }_{xy}.\end{array}\right\} $ $ \left.\begin{array}{l}{\varepsilon}_{x}=-\frac{\partial {w}_{x}}{\partial x}, {\gamma }_{yz}=-(\frac{\partial {w}_{y}}{\partial z}+\frac{\partial {w}_{z}}{\partial y}), \\ {\varepsilon}_{y}=-\frac{\partial {w}_{y}}{\partial y}, {\gamma }_{zx}=-(\frac{\partial {w}_{z}}{\partial x}+\frac{\partial {w}_{x}}{\partial z}), \\ {\varepsilon }_{z}=-\frac{\partial {w}_{z}}{\partial z}, {\gamma }_{xy}=-(\frac{\partial {w}_{x}}{\partial y}+\frac{\partial {w}_{y}}{\partial x}).\end{array}\right\} $， 注：式中：G为剪切模量；υ为泊松比；wx、wy和wz分别x、y和z方向的位移；βT为热膨胀系数；K为体积模量，其与剪切模量和泊松比的关系为$ K=\frac{2G(1+\nu)}{3(1+2\nu)} $；γsat为饱和重度；σ为总应力；σ´为有效应力；εx、εy和εz分别为x、y和z方向的应变；$ {\varepsilon }_{v}={\varepsilon }_{x}+{\varepsilon }_{y}+{\varepsilon }_{z} $为体应变；τ为剪应力；γ为剪应变.
下载: 导出CSV
表 6 模型参数取值
Table 6. Model parameters
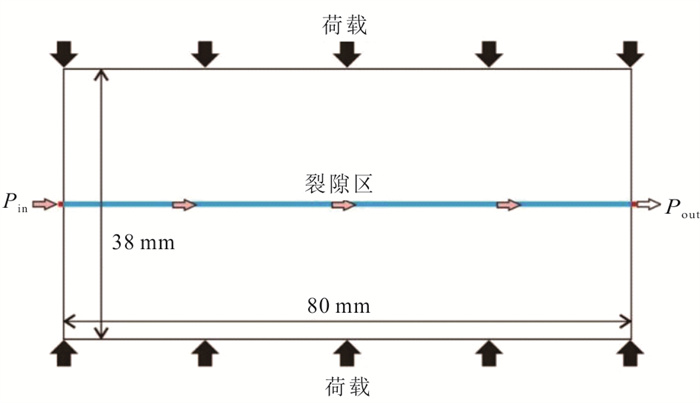
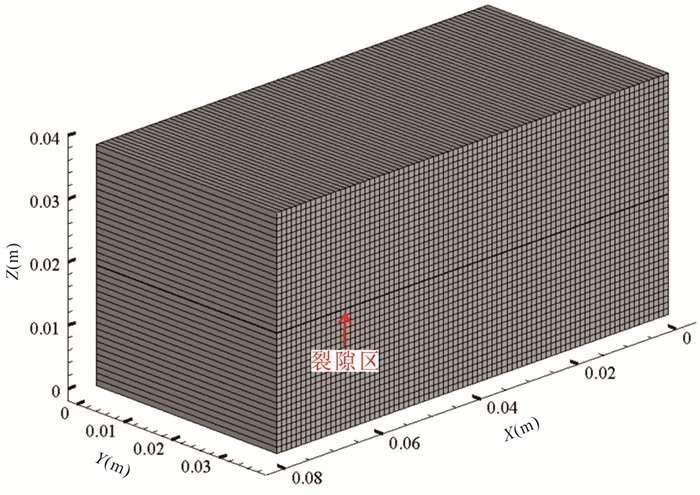
参数 取值 模型尺寸(X×Y×Z), m3 0.08×0.038×0.038 裂隙初始开度, m 4.03×10‒6 裂隙初始渗透率, m2 1.35×10‒12 基质渗透率, m2 1.00×10‒20 基质孔隙度 0.03 裂隙孔隙度 0.60 动力粘滞系数, kg·m‒1s‒1 8.9×10‒3 杨氏模量, GPa 50.0 泊松比 0.20 Biot系数 1.0 应力荷载, MPa 5~40
下载: 导出CSV
-
Cai, J. L., Zhou, Z. F., 2009. Review of Seepage Research in Rough Fractures. Site Investigation Science and Technology, (4): 18-23 (in Chinese with English abstract). Chen, Y. F., Zhou, J. Q., Hu, S. H., et al., 2015. Evaluation of Forchheimer Equation Coefficients for Non⁃Darcy Flow in Deformable Rough⁃Walled Fractures. Journal of Hydrology, (529): 993-1006. Gao, H. M., Lan, Y. W., Zhao, Y. L., et al., 2017. Study on Permeability of Granite under Conditions of Stress and Temperature. Journal of Jiamusi University (Natural Science Edition), 35(6): 955-958 (in Chinese with English abstract). doi: 10.3969/j.issn.1008-1402.2017.06.019 Guo, Q. H., He, T., Zhuang, Y. Q., et al., 2020. Expansion of Fracture Network in Granites via Chemical Stimulation: A Laboratory Study. Earth Science Frontiers, 27(1): 159-169 (in Chinese with English abstract). He, Y. L., Yang, L. Z., 2004. Testing Study on Variational Characteristics of Rockmass Permeability under Loading⁃Unloading of Confining Pressure. Chinese Journal of Rock Mechanics and Engineering, 23(3): 415-419 (in Chinese with English abstract). doi: 10.3321/j.issn:1000-6915.2004.03.010 Huang, Y. H., Lei, H. W., Bai, B., et al., 2020. Multiphysics⁃Coupling Simulation Technologies and Their Application in Safety Assessment of Geothermal Exploration. Science & Technology for Development, 16(S1): 323-331 (in Chinese with English abstract). Huang, Y. Z., Wang, E. Z., 2007. Experimental Study of the Laws between the Effective Confirming Pressure and Rock Permeability. Journal of Tsinghua University (Science and Technology), 47(3): 340-343 (in Chinese with English abstract). Lei, H. W., 2014. Coupled Hydrothermal Process Analysis of Thermal Energy Exploitation Mechanics in Enhanced Geothermal System (EGS). Jilin University, Changchun (in Chinese). Li, J., Zhang, Y., Hu, D. W., et al., 2019. Gas Permeability of Granite in Triaxial Cyclic Loading/Unloading Tests. Rock and Soil Mechanics, 40(2): 693-700 (in Chinese with English abstract). Li, L. L., Zhu, J. F., Jing, H. W., et al., 2021. Study on Evolution of Granite Permeability under Stress after High Temperature Exposure. Coal Science and Technology, 49(7): 45-50 (in Chinese with English abstract). Meng, X., Liu, W., Meng, T., 2018. Experimental Investigation of Thermal Cracking and Permeability Evolution of Granite with Varying Initial Damage under High Temperature and Triaxial Compression. Advances in Materials Science & Engineering, (4): 1-9. https://doi.org/10.1155/2018/8759740 Meng, X. L., Meng, F. Q., Li, H. S., et al., 2020. Analysis on Non⁃Darcy Flow Characteristic for Fractured Rock. The Chinese Journal of Geological Hazard and Control, 31(4): 121-125 (in Chinese with English abstract). Mi, Z. X., Wang, F. G., Shi, N., et al., 2018. Experimental Study on Effect of Multi⁃Stage Stress Variations on Permeability and Pore Structure of Sandstone. Chinese Journal of Geotechnical Engineering, 40(5): 864-871 (in Chinese with English abstract). Na, J., 2016. Study on the Effect of Chemical Stimulation Technology on Enhanced Geothermal System (EGS) Thermal Reservoir Reconstruction. Jilin University, Changchun (in Chinese). Nara, Y., Kato, M., Fukuda, D., et al., 2018. Permeability of Granite Including Macro⁃Fracture Naturally Filled with Fine⁃Grained Minerals. Pure & Applied Geophysics, 175(3): 917-927. https://doi.org/10.1007/s00024⁃017⁃1704⁃x Pyrak⁃Nolte, L. J., Nolte, D. D., 2016. Approaching a Universal Scaling Relationship between Fracture Stiffness and Fluid Flow. Nature Communication, 7: 10663. https://doi.org/10.1038/ncomms10663 Selvadurai, A. P. S., 2015. Normal Stress⁃Induced Permeability Hysteresis of a Fracture in a Granite Cylinder. Geofluids, 15(1-2): 7-47. https://doi.org/10.1111/gfl.12107 Wang, B., Zhao, R., Li, Y. S., et al., 2021. Experimental Study on Variation Characteristics of Rock Permeability under Different Confining Pressures in Western Sichuan Plateau—Taking Balang Mountain Tunnel as an Example. Safety and Environmental Engineering, 28(3): 179-186 (in Chinese with English abstract). Wang, F. G., Sun, Z. J., Liu, H. Y., et al., 2016. Experimental Study on the Variation of Permeability of Medium⁃Fine Feldspar⁃Quartz Sandstone Low⁃Permeability Reservoir under the Circulatory Increasing or Reducing Conditions of Confining Pressure. Journal of Hydraulic Engineering, 47(9): 1125-1132 (in Chinese with English abstract). Wang, L. C., Cardenas, M. B., 2016. Development of an Empirical Model Relating Permeability and Specific Stiffness for Rough Fractures from Numerical Deformation Experiments. Journal of Geophysical Research⁃Solid Earth, 121(7): 4977-4989. https://doi.org/10.1002/2016JB013004 Wang, M. D., Guo, Q. H., Yan, W. D., et al., 2014. Medium⁃Low⁃Enthalpy Geothermal Power⁃Electricity Generation at Gonghe Basin, Qinghai Province. Earth Science, 39(9): 1317-1322 (in Chinese with English abstract). Wu, Z. S., Feng, Z. J., Shi, X. D., et al., 2020. Study on Permeability of Granite under Different Confining Pressures and Its Permeability Sensitivity. Mining Research and Development, 40(10): 46-50 (in Chinese with English abstract). Xin, L. W., Sun, K. M., Li, T. S., 2017. Probe to the Permeability Variation Regularity of the Fractured Core Rock under the Impact of Loading and Unloading Vibrations. Journal of Safety and Environment, 17(1): 72-75 (in Chinese with English abstract). Yu, H. D., Chen, F. F., Chen, W. Z., et al., 2012. Research on Permeability of Fractured Rock. Chinese Journal of Rock Mechanics and Engineering, 31(S1): 2788-2795 (in Chinese with English abstract). Zhang, F., Wang, L., Zhao, J. J., et al., 2016. Evolution of Permeability of Granite with Tensile and Compressive⁃Shear Cracks. Rock and Soil Mechanics, 37(10): 2803-2809 (in Chinese with English abstract). Zhang, P. S., Hou, J. Q., Zhao, C. Y., et al., 2020a. Experimental Study on Seepage Characteristics of Red Sandstone with Different Confining Pressures and Different Damage Degrees. Chinese Journal of Rock Mechanics and Engineering, 39(12): 2405-2415 (in Chinese with English abstract). Zhang, P. S., Zhao, C. Y., Hou, J. Q., et al., 2020b. Experimental Study on Seepage Characteristics of Deep Sandstone under Temperature⁃Stress⁃Seepage Coupling Conditions. Chinese Journal of Rock Mechanics and Engineering, 39(10): 1957-1974 (in Chinese with English abstract). Zhang, S. Q., Li, X. F., Song, J., et al., 2021. Analysis on Geophysical Evidence for Existence of Partial Melting Layer in Crust and Regional Heat Source Mechanism for Hot Dry Rock Resources of Gonghe Basin. Earth Science, 46(4): 1416-1436 (in Chinese with English abstract). 蔡金龙, 周志芳, 2009. 粗糙裂隙渗流研究综述. 勘察科学技术, (4): 18-23. https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX200904004.htm 高红梅, 兰永伟, 赵延林, 等, 2017. 花岗岩在围压和温度作用下渗透率变化规律研究. 佳木斯大学学报(自然科学版), 35(6): 955-958. https://www.cnki.com.cn/Article/CJFDTOTAL-JMDB201706019.htm 郭清海, 何曈, 庄亚芹, 等, 2020. 化学刺激法提高花岗岩类岩石裂隙渗透性的实验研究. 地学前缘, 27(1): 159-169. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY202001020.htm 贺玉龙, 杨立中, 2004. 围压升降过程中岩体渗透率变化特性的试验研究. 岩石力学与工程学报, 23(3): 415-419. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200403010.htm 黄永辉, 雷宏武, 白冰, 等, 2020. 多场耦合模拟技术及其在地热开采安全性评价中的应用. 科技促进发展, 16(S1): 323-331. https://www.cnki.com.cn/Article/CJFDTOTAL-KJCJ2020Z1014.htm 黄远智, 王恩志, 2007. 低渗透岩石渗透率与有效围压关系的实验研究. 清华大学学报(自然科学版), 47(3): 340-343. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB200703009.htm 雷宏武, 2014. 增强型地热系统(EGS)中热能开发力学耦合水热过程分析(博士学位论文). 长春: 吉林大学. 李军, 张杨, 胡大伟, 等, 2019. 花岗岩三轴循环加卸载条件下的气体渗透率. 岩土力学, 40(2): 693-700. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902032.htm 李林林, 朱俊福, 靖洪文, 等, 2021. 高温处理后花岗岩应力作用下渗透特性演化研究. 煤炭科学技术, 49(7): 45-50. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ202107006.htm 蒙学礼, 蒙发强, 李涣森, 等, 2020. 裂隙岩体非线性渗流特性分析. 中国地质灾害与防治学报, 31(4): 121-125. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH202004017.htm 秘昭旭, 王福刚, 石娜, 等, 2018. 多期次应力变化对砂岩渗透率和孔隙结构影响的试验研究. 岩土工程学报, 40(5): 864-871. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805014.htm 那金, 2016. 化学刺激技术对增强型地热系统(EGS)热储层改造作用研究(博士学位论文). 长春: 吉林大学. 王彪, 赵瑞, 李云松, 等, 2021. 不同围压作用下川西高原地区岩石渗透率变化特性试验研究——以巴郎山隧道为例. 安全与环境工程, 28(3): 179-186. https://www.cnki.com.cn/Article/CJFDTOTAL-KTAQ202103024.htm 王福刚, 孙兆军, 刘红艳, 等, 2016. 中-细粒长石石英砂岩低渗储层在围压循环增减条件下渗透率变化规律的试验研究. 水利学报, 47(9): 1125-1132. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201609004.htm 王敏黛, 郭清海, 严维德, 等, 2014. 青海共和盆地中低温地热流体发电. 地球科学, 39(9): 1317-1322. doi: 10.3799/dqkx.2014.113?viewType=HTML 武治盛, 冯子军, 石晓巅, 等, 2020. 不同围压下花岗岩渗透率及其渗透敏感性规律研究. 矿业研究与开发, 40(10): 46-50. https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202010009.htm 辛利伟, 孙可明, 李天舒, 2017. 加卸载作用下裂隙岩芯渗透性变化规律研究. 安全与环境学报, 17(1): 72-75. https://www.cnki.com.cn/Article/CJFDTOTAL-AQHJ201701018.htm 于洪丹, 陈飞飞, 陈卫忠, 等, 2012. 含裂隙岩石渗流力学特性研究. 岩石力学与工程学报, 31(S1): 2788-2795. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2012S1024.htm 张帆, 王亮, 赵建建, 等, 2016. 花岗岩张拉和压剪裂隙渗透率演化研究. 岩土力学, 37(10): 2803-2809. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201610009.htm 张培森, 侯季群, 赵成业, 等, 2020a. 不同围压不同损伤程度红砂岩渗流特性试验研究. 岩石力学与工程学报, 39(12): 2405-2415. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202012003.htm 张培森, 赵成业, 侯季群, 等, 2020b. 温度-应力-渗流耦合条件下红砂岩渗流特性试验研究. 岩石力学与工程学报, 39(10): 1957-1974. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202010002.htm 张森琦, 李旭峰, 宋健, 等, 2021. 共和盆地壳内部分熔融层存在的地球物理证据与干热岩资源区域性热源分析. 地球科学, 46(4): 1416-1436. doi: 10.3799/dqkx.2020.094?viewType=HTML -
点击查看大图
图(9) / 表(6)
计量
- 文章访问数: 411
- HTML全文浏览量: 150
- PDF下载量: 44
- 被引次数: 0
