Blasting-Induced Peak Particle Velocity Prediction of Hole-by-Hole Blasting Operation Using Digital Electronic Detonator in Open-Pit Mine
-
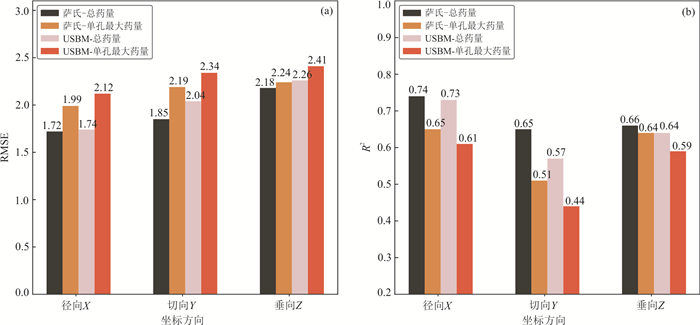
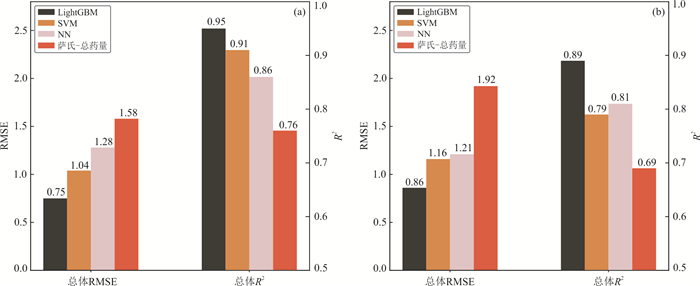
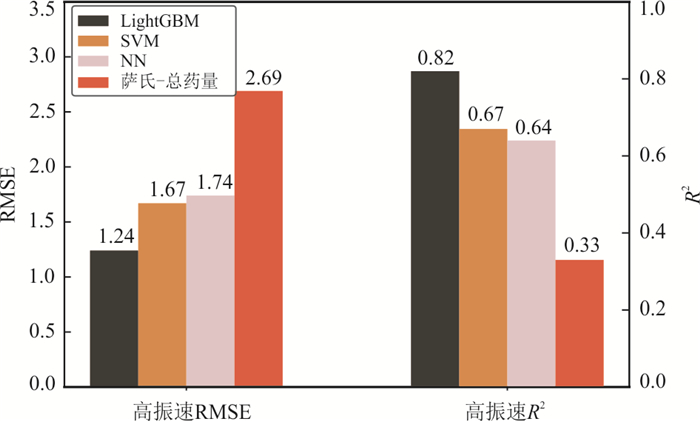
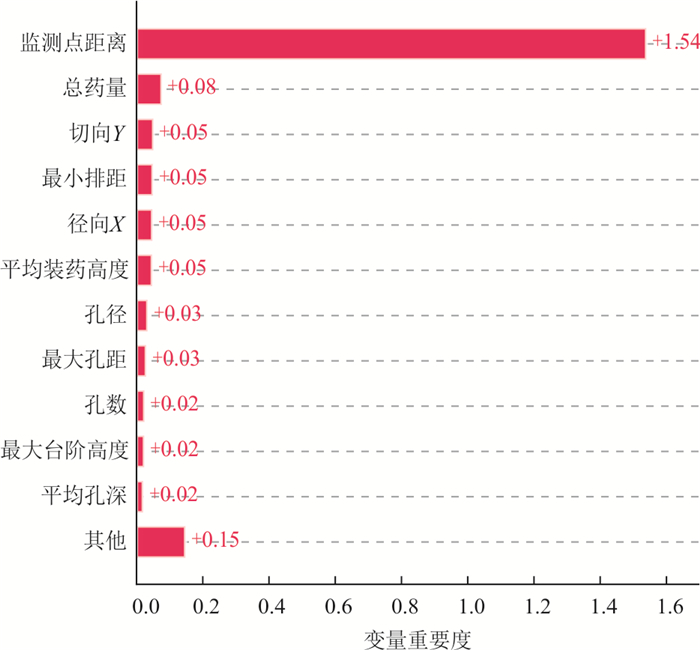
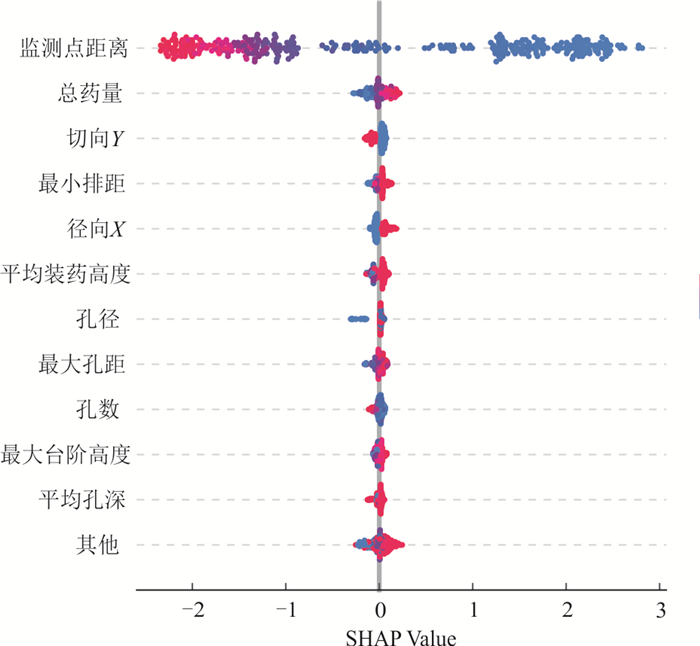
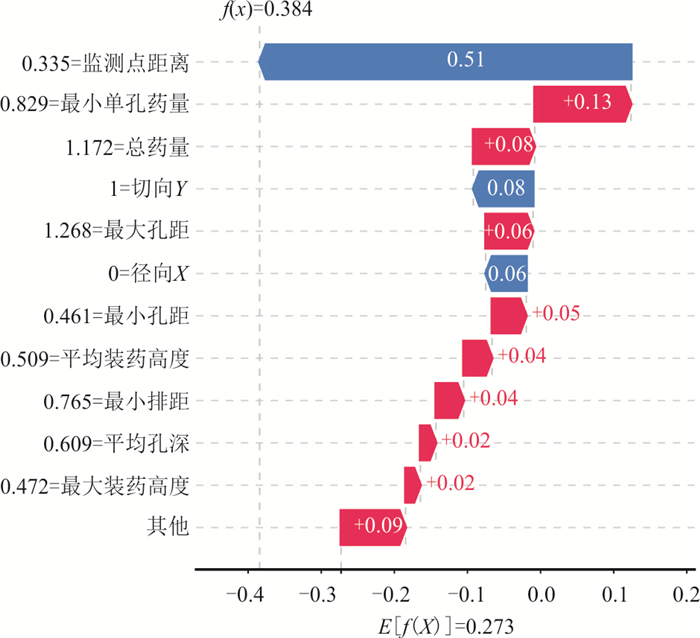
摘要: 针对目前露天矿爆破质点峰值振速预测研究存在模型可解释性不足、不适用于数码电子雷管逐孔起爆条件等问题，通过现场试验记录每孔爆破参数与测取爆破振动信号，结合轻型梯度提升机（LightGBM）算法与SHAP模型可解释性框架，建立了露天矿数码电子雷管逐孔起爆条件下的三轴质点峰值振速预测模型.从测试集均方根误差RMSE和拟合优度R2而言，LightGBM总体RMSE相比于支持向量机与神经网络分别降低了25.9%和28.9%，总体R2分别提高了12.7%和9.9%.LightGBM与萨道夫斯基经验公式相比，RMSE在径向X、切向Y和垂向Z上分别降低了63.4%、39.5%和68.3%，R2分别提高了18.9%、27.7%和42.4%.除方向轴变量外，监测点距离、总药量、最小排距、平均装药长度、孔径与最大孔距为对质点峰值振速影响程度最大的6个变量，其中监测点距离与质点峰值振速为负相关关系，总药量、最小排距、平均装药高度与最大孔距则与质点峰值振速呈正相关关系.Abstract: Current research on blasting-induced peak particle velocity prediction in open-pit mines is infeasible for the hole-by-hole blasting operation using digital electronic detonators, and its models lack interpretability. By recording the blasting parameters for each blasthole and measuring the induced triaxial particle velocity, a model to predict the triaxial peak particle velocity is established based on LightGBM, and SHAP is introduced to interpret the variable importance of the model. Regarding the root mean squared error RMSE and goodness of fitting R2 on the test set, the established LightGBM model outperforms the support vector machine and neural network models as its RMSE decreases by 25.9% and 28.9%, while the R2 improves by 12.7% and 9.9%. Compared to the Sadaovsk empirical formula, which is widely applied to the blasting design and safety evaluation, the RMSE of LightGBM declines by 63.4%, 39.5% and 68.3%, while the R2 increases by 18.9%, 27.7%and 42.4% in the longitudinal axis X, transverse axis Y and vertical axis Z, respectively. The SHAP values computed from the model inform that apart from the axis variable, the distance between blasting source and monitoring point, total charge, the minimum row distance, the average charge length, hole diameter and the maximum hole distance are the six most influencing variables that affect the predicted value of peak particle velocity. The distance between blasting source and monitoring point is negatively correlated with the predicted peak particle velocity, while the other five variables are positively correlated with the predicted value.
-
图 2 经验公式测试集RMSE与R2对比
Fig. 2. Test set RMSE and R2 of the empirical formulas
a.RMSE; b.R2
图 3 训练集与测试集模型总体RMSE与R2对比
a.训练集；b.测试集
Fig. 3. Training set and test set RMSE and R2 of the models
图 4 测试集模型真实值‒预测值散点图
a.LightGBM；b.SVM；c.NN；d.萨氏公式
Fig. 4. Test set actual PPV versus predicted PPV
图 5 测试集模型三轴RMSE与R2对比
Fig. 5. Test set triaxial RMSE and R2 of the models
a. RMSE; b. R2
表 1 爆破质点峰值振速记录例表
Table 1. Example sheet of recorded peak particle velocity
监测点位置 监测点距离(m) 径向X峰值振速(cm/s) 切向Y峰值振速(cm/s) 垂向Z峰值振速(cm/s) 宿舍楼 1 758 0.15 0.20 0.19 办公楼 1 635 0.16 0.16 0.16 锅炉房 1 567 0.21 0.23 0.19 变电站 1 545 0.24 0.25 0.30 现场1 73.7 4.11 4.17 9.65 现场2 155.5 2.92 2.14 2.89 
下载: 导出CSV
表 2 爆破参数记录例表
Table 2. Example sheet of recorded blasting parameters
孔号 孔径(mm) 台阶高度(m) 孔深(m) 孔距/排距(m) 药量(kg) 装药高度(m) 填塞长度(m) 1 250 15.7 18.2 17/9.5 687 10.9 7.5 2 250 15.6 18.1 17/9.5 680 10.8 7.5 3 250 15.8 18.3 17/9.5 693 11 7.5 4 250 15.5 18.0 17/9.5 674 10.7 7.5 5 250 15.7 18.2 17/9.5 693 11 7.5 ······ 50 250 15.6 18.1 17/9.5 680 10.8 7.5
下载: 导出CSV
表 3 模型变量
Table 3. Modeling variables
原始变量 模型变量 质点峰值振速 对数质点峰值振速 监测点距离 监测点距离 孔径 孔径 孔数 孔数 坐标轴 径向X独热编码 切向Y独热编码 垂向Z独热编码 单孔装药量 最大单孔装药量 平均单孔装药量 最小单孔装药量 总药量 台阶高度 最大台阶高度 平均台阶高度 最小台阶高度 孔深 最大孔深 平均孔深 最小孔深 孔距 最大孔距 平均孔距 最小孔距 排距 最大排距 平均排距 最小排距 装药高度 最大装药高度 平均装药高度 最小装药高度 填塞长度 最大填塞长度 平均填塞长度 最小填塞长度
下载: 导出CSV
表 4 LightGBM超参数
Table 4. Hyperparameters of LightGBM
超参数 参数取值 迭代次数 90 学习率 0.06 约束系数$ \gamma $ 0.05 约束系数$ \lambda $ 0.1 最大叶节点数 50 最大深度 6 每次迭代选用变量比例 1 直方图离散区间最大数目 255 直方图离散区间最小样本数 3 叶节点最小Hessian值之和 1e-3 数据重抽样步长 5 数据重抽样比例 0.5
下载: 导出CSV
表 5 SVM超参数
Table 5. Hyperparameters of SVM
超参数 参数取值 核函数形式 径向基核函数RBF RBF核函数gamma值 0.05 惩罚系数 4 容忍度 1e-3
下载: 导出CSV
表 6 NN超参数
Table 6. Hyperparameters of NN
超参数 参数取值 激活函数形式 tanh 隐含层神经元个数 30 隐含层层数 4 L2正则项系数 1e-4 学习率 1e-3 容忍度 1e-4
下载: 导出CSV
-
Aladejare, A. E., Lawal, A. I., Onifade, M., 2022. Predicting the Peak Particle Velocity from Rock Blasting Operations Using Bayesian Approach. Acta Geophysica, 70(2): 581-591. https://doi.org/10.1007/s11600-022-00727-5 Hao, H. Z., Gu, Q., Hu, X. M., 2021. Research Advances and Prospective in Mineral Intelligent Identification Based on Machine Learning. Earth Science, 46(9): 3091-3106 (in Chinese with English abstract). He, J., Chalise, P., 2020. Nested and Repeated Cross Validation for Classification Model with High-Dimensional Data. Revista Colombiana de Estadística, 43(1): 103-125. doi: 10.15446/rce.v43n1.80000 He, L., Yang, R. S., Zhong, D. W., et al., 2021. Calculation of Equivalent Charge Weight Per Delay and Vibration Velocity Prediction for Millisecond Delay Blasting. Explosion and Shock Waves, 41(9): 129-141 (in Chinese with English abstract). Hosseini, S. A., Tavana, A., Abdolahi, S. M., et al., 2019. Prediction of Blast-Induced Ground Vibrations in Quarry Sites: A Comparison of GP, RSM and MARS. Soil Dynamics and Earthquake Engineering, 119: 118-129. doi: 10.1016/j.soildyn.2019.01.011 Jiao, H., Du, X., Zhao, M., et al., 2021. Nonlinear Seismic Response of Rock Tunnels Crossing Inactive Fault under Obliquely Incident Seismic P Waves. Journal of Earth Science, 32(5): 1174-1189. doi: 10.1007/s12583-021-1483-2 Ke, G., Meng, Q., Finley, T., et al., 2017. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, California. Li, W. B., Fan, X. M., Huang, F. M., et al., 2021. Uncertainties of Landslide Susceptibility Modeling under Different Environmental Factor Connections and Prediction Models. Earth Science, 46(10): 3777-3795 (in Chinese with English abstract). http://www.sciencedirect.com/science/article/pii/S0341816221001090 Lundberg, S. M., Erion, G. G., Lee, S. I., 2018. Consistent Individualized Feature Attribution for Tree Ensembles. Methods, 5(13): 25. http://arxiv.org/pdf/1802.03888 Lundberg, S. M., Lee, S. I., 2017. A Unified Approach to Interpreting Model Predictions. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, California. Tian, X., Song, Z., Wang, J., 2019. Study on the Propagation Law of Tunnel Blasting Vibration in Stratum and Blasting Vibration Reduction Technology. Soil Dynamics and Earthquake Engineering, 126: 105813. https://doi.org/10.1016/j.soildyn.2019.105813 Trivedi, R., Singh, T., Raina, A., 2014. Prediction of Blast-Induced Flyrock in Indian Limestone Mines Using Neural Networks. Journal of Rock Mechanics and Geotechnical Engineering, 6(5): 447-454. doi: 10.1016/j.jrmge.2014.07.003 Yang, X., Zhang, Y. P., Li, Y., et al., 2017. Analysis of Seismic Wave Propagation Law of Multi-Step Terrain Blasting and Correction of Blasting Vibration Velocity Prediction Formula. Mining Research and Development, 37(5): 78-83 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-KYYK201705017.htm Zhang, G. C., Guo, L. J., Jia, J. J., et al., 2020. Response Characteristics of Blasting Vibration to Rock Slope in an Open-Pit Iron Mine. China Mining Magazine, 29(12): 165-169 (in Chinese with English abstract). Zhang, W., Li, H., Li, Y. et al, 2021a. Application of Deep Learning Algorithms in Geotechnical Engineering: A Short Critical Review. Artificial Intelligence Review, 54: 5633-5673. https://doi.org/10.1007/s10462-021-09967-1 Zhang, X., Peng, X., Li, X., et al., 2021b. Three- Dimensional Seismic Response in Complex Site Conditions: A New Approach Based on an Auxiliary-Model Method. Journal of Earth Science, 32 (5): 1152-1165. doi: 10.1007/s12583-021-1471-6 Zhang, W., Phoon, K. K., 2022. Editorial for Advances and Applications of Deep Learning and Soft Computing in Geotechnical Underground Engineering. Journal of Rock Mechanics and Geotechnical Engineering, 14(3): 671-673. doi: 10.1016/j.jrmge.2022.01.001 Zhang, Y. P., Yang, X., Zhu, X. X., 2018. Critical Velocity and Safety Distance Calculation under Influence of Blasting Vibration. Industrial Minerals & Processing, 47(8): 28-30 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-HGKJ201808007.htm Zhou, J. R., Lu, W. B., Yan, P., et al., 2016. Frequency-Dependent Attenuation of Blasting Vibration Waves. Rock Mechanics and Rock Engineering, 49(10): 4061-4072. https://doi.org/10.1007/s00603-016-1046-5 Zhu, M., Hu, X. T., Feng, Z. W., et al., 2021. Optimization of Blasting Vibration Velocity Attenuation Model under the Condition of Soil-Rock Strata. Science Technology and Engineering, 21(10): 4211-4218 (in Chinese with English abstract). 郝慧珍, 顾庆, 胡修棉, 2021. 基于机器学习的矿物智能识别方法研究进展与展望. 地球科学, 46(9): 3091-3106. doi: 10.3799/dqkx.2020.360 何理, 杨仁树, 钟东望, 等, 2021. 毫秒延时爆破等效单响药量计算及振速预测. 爆炸与冲击, 41(9): 129-141. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ202109011.htm 李文彬, 范宣梅, 黄发明, 等, 2021. 不同环境因子联接和预测模型的滑坡易发性建模不确定性. 地球科学, 46(10): 3777-3795. doi: 10.3799/dqkx.2021.042 杨曦, 张云鹏, 李岩, 等, 2017. 多台阶地形爆破地震波传播规律分析及爆破振速预测公式修正. 矿业研究与开发, 37(5): 78-83. https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK201705017.htm 张耿城, 郭连军, 贾建军, 等, 2020. 某露天铁矿爆破振动对边坡的动态响应特征研究. 中国矿业, 29(12): 165-169. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKA202012028.htm 张云鹏, 杨曦, 朱晓玺, 2018. 爆破振动影响下露天边坡临界振速及安全距离计算. 化工矿物与加工, 47(8): 28-30. https://www.cnki.com.cn/Article/CJFDTOTAL-HGKJ201808007.htm 朱明, 胡鑫涛, 冯志威, 等, 2021. 土岩复合地层条件下爆破振速衰减模型优选. 科学技术与工程, 21(10): 4211-4218. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS202110050.htm -
点击查看大图
图(9) / 表(6)
计量
- 文章访问数: 411
- HTML全文浏览量: 339
- PDF下载量: 26
- 被引次数: 0
