边坡勘察钻孔信息价值评价及优化布置方法

胡金政; 张洁; 黄宏伟; 郑建国

doi:10.3799/dqkx.2022.216

边坡勘察钻孔信息价值评价及优化布置方法

doi: 10.3799/dqkx.2022.216

胡金政^{1, 3, ,},
张洁^1, , ,,
黄宏伟¹,
郑建国^{2, 3}

1.
同济大学地下建筑与工程系, 上海 200092
2.
机械工业勘察设计研究院有限公司, 陕西西安 710043
3.
陕西省特殊岩土性质与处理重点实验室, 陕西西安 710043

基金项目:

国家自然科学基金资助项目 42072302

国家自然科学基金资助项目 41672276

详细信息

作者简介:
胡金政(1994-), 男, 博士研究生, 从事岩土工程不确定性研究.ORCID: 0000-0002-6058-8083.E-mail: tjcce_hujz@tongji.edu.cn

通讯作者:
张洁, ORCID: 0000-0001-7528-4077.E-mail: cezhangjie@tongji.edu.cn

中图分类号: P642
计量
- 文章访问数: 782
- HTML全文浏览量: 608
- PDF下载量: 67
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-28
- 网络出版日期: 2023-06-06
- 刊出日期: 2023-05-25

Value of Information Assessment and Optimization of Slope Boreholes

Hu Jinzheng^{1, 3
,
,},
Zhang Jie^{1
, ,
,},
Huang Hongwei¹,
Zheng Jianguo^{2, 3}

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
China Jikan Research Institute of Engineering Investigations and Design Co. Ltd., Xi'an 710043, China
3.
Shaanxi Key Laboratory for the Property and Treatment of Special Soil and Rock, Xi'an 710043, China

摘要

摘要: 为了解决现有边坡勘察试验钻孔布置的优化方法概念复杂、计算量大，需要预先定量估计边坡失稳损失，在实际应用中不方便的问题，利用边坡响应面机器学习模型提出了一种边坡勘察方案的信息价值量化指标，进而给出了边坡钻孔布置方案优化方法.利用边坡部分特征响应面模型建立了安全系数与勘察数据之间的关系.利用随机模拟样本即可实现对边坡勘察钻孔方案的信息价值量化指标计算，分析不同勘察方案时不需要额外重复计算安全系数，大幅提高了分析效率.基于提出的方法，对不排水边坡案例进行了分析，分析结果与文献中相似，算法复杂度和计算量大幅降低.本方法可以快速评价和对比边坡勘察方案的信息价值，进而实现钻孔布置方案优化，具有概念清晰、算法简单、计算方便的特点，计算量也相比传统方法大幅降低，易于工程勘察设计人员接受和采用.
- 边坡安全系数 /
- 钻孔 /
- 空间变异性 /
- 勘察方案优化 /
- 岩土工程 /
- 工程地质
Abstract: The conventional method to optimize the slope investigation program is usually assigned with complicated concept and arduous computational efforts. Also, the quantitative evaluation of slope failure loss is required, which is not convenient in practice. In this paper it aims to solve the above problem with a suggested method based on training of response surface-based machine learning model with incomplete features. The relationship between the factor of safety and the site investigation data is established. Then a prediction function is imported and calibrated with simulated samples. This method adopts the root mean square error of factor of safety as the indicator to assess the effectiveness of slope borehole program. The algorithm is provided and applied in an illustrative example of an undrained slope. The results accord well with those reported in literatures. The suggested method provides an efficient way to assess the effectiveness of site investigation program for slope. It has the characteristics of clear concept, simple algorithm and convenient calculation. Also the computational efforts are greatly reduced. This method will be more acceptable for practitioners.
- safety factor of slope /
- borehole /
- spatial variability /
- optimization of site investigation program /
- geotechnical engineering /
- engineering geology

HTML全文

图 1 参数向量w的取值空间关系

Fig. 1. The relationship of the spaces of the coefficient vector w

下载: 全尺寸图片幻灯片

图 2 生成安全系数训练样本算法流程

Fig. 2. Flow chart for generating training samples of factor of safety

下载: 全尺寸图片幻灯片

图 3 不排水饱和粘土边坡有限差分数值分析模型

Fig. 3. The finite difference model of the undrained-clay slope

下载: 全尺寸图片幻灯片

图 4 未经Q₀标准化的信息价值指标

Fig. 4. The unnormalized indicator of the value of information

下载: 全尺寸图片幻灯片

图 5 经Q₀标准化后的信息价值指标

Fig. 5. The normalized indicator of the value of information

下载: 全尺寸图片幻灯片

图 6 信息价值指标随钻孔位置的变化

Fig. 6. V(SIP) or V_m(SIP) as a function of borehole location

下载: 全尺寸图片幻灯片

图 7 信息价值指标计算量与文献中指标相比较

Fig. 7. Comparison between the value of information in this paper and indicators in the literatures

下载: 全尺寸图片幻灯片

图 8 两个钻孔时所有的V_m(SIP)数据点

Fig. 8. All points of V_m(SIP) with two boreholes

下载: 全尺寸图片幻灯片

图 9 不同模拟次数N条件下计算的信息价值指标随钻孔位置的变化

Fig. 9. V_m(SIP) as a function of borehole location with various number of simulations N

下载: 全尺寸图片幻灯片

表 1 各方法计算时间对比(使用FLAC3D进行边坡稳定性分析共60个备选勘察方案)

Table 1. Comparison of the time consumption of different methods (analyzing 60 alternatives of site investigation program with FLAC3D)

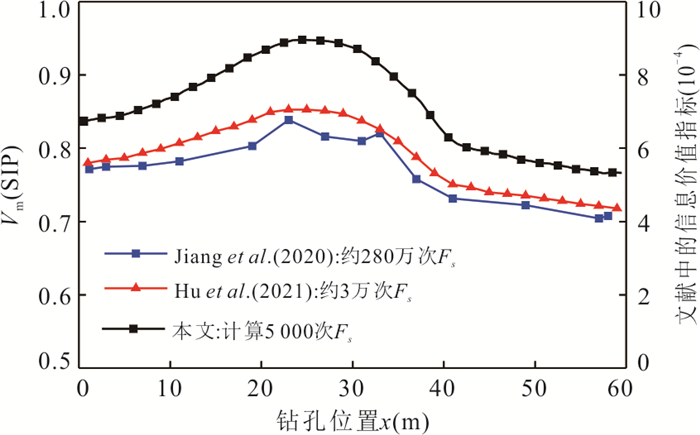
方法	计算类型	每次计算失效概率的边坡稳定性分析次数	每个勘察方案计算失效概率次数	边坡稳定性分析总次数	总时间估算
传统蒙特卡罗方法	判断是否失稳	10万	200	12亿	约304.4年
Jiang et al. (2020)方法	计算安全系数	至少1 000	200	至少1 200万	至少22.83年
Hu et al. (2021)方法	判断是否失稳	3万	3万	3万	约2.78天
本文方法	计算安全系数	-	-	5 000	约3.47天
注：此处未包含后处理计算信息价值的时间；本文和Hu et al. (2021)方法对不同失效概率、不同勘察方案不需要重复边坡稳定性分析.

下载: 导出CSV

参考文献(45)

Au, S. K., Beck, J. L., 2001. Estimation of Small Failure Probabilities in High Dimensions by Subset Simulation. Probabilistic Engineering Mechanics, 16(4): 263-277. doi: 10.1016/S0266-8920(01)00019-4
Blitzstein, J. K., Hwang, J., 2019. Introduction to Probability (2nd Edition). Chapman and Hall/CRC, New York.
Cho, S.E., 2010. Probabilistic Assessment of Slope Stability That Considers the Spatial Variability of Soil Properties. Journal of Geotechnical and Geoenvironmental Engineering, 136(7): 975-984. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000309
Fu, F.Y., Zheng, X.Y., Lü, Q., et al., 2014. Second Order Reliability Analysis of Slope Stability Using Response Surface Method. Rock and Soil Mechanics, 35(12): 3460-3466 (in Chinese with English abstract).
Goldsworthy, J.S., Jaksa, M.B., Fenton, G.A., et al., 2007. Effect of Sample Location on the Reliability Based Design of Pad Foundations. Georisk, 1(3): 155-166. http://www.onacademic.com/detail/journal_1000037205077710_de8a.html
Gong, W., Juang, C.H., Wasowski, J., 2021. Geohazards and Human Settlements: Lessons Learned from Multiple Relocation Events in Badong, China: Engineering Geologist's Perspective. Engineering Geology, 285: 106051. doi: 10.1016/j.enggeo.2021.106051
Gong, W., Luo, Z., Juang, C.H., et al., 2014. Optimization of Site Exploration Program for Improved Prediction of Tunneling-Induced Ground Settlement in Clays. Computers and Geotechnics, 56: 69-79. https://doi.org/10.1016/j.compgeo.2013.10.008
Green, S.B., 1991. How Many Subjects does It Take to do a Regression Analysis. Multivariate Behavioral Research, 26(3): 499-510. https://doi.org/10.1207/s15327906mbr2603_7
He, C., Tang, H. M., Shen, P. W., et al., 2021. Progressive Failure Mode and Stability Reliability of Strain-Softening Slope. Earth Science, 46(2): 697-707 (in Chinese with English abstract).
Hu, J.Z., Zhang, J., Huang, H.W., et al., 2021. Value of Information Analysis of Site Investigation Program for Slope Design. Computers and Geotechnics, 131: 103938. https://doi.org/10.1016/j.compgeo.2020.103938
Itasca Consulting Group, 2019. FLAC3D-Fast Lagrangian Analysis of Continua in Three-Dimensions, Ver. 7.0. Itasca, Minneapolis.
Jiang, S.H., Li, D.Q., Cao, Z.J., et al., 2015. Multiple Response Surfaces Method for Probabilistic Analysis and Reliability Sensitivity Analysis of Slopes Considering Spatially Varying Soil Properties. Journal of Disaster Prevention and Mitigation Engineering, 35(5): 592-598 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DZXK201505007.htm
Jiang, S.H., Liu, X., Yao, R.Z., et al., 2018. Optimization Design Approach for Layout Scheme of Slope Boreholes Based on Bayesian Updating and Value of Information Analysis. Chinese Journal of Geotechnical Engineering, 40(10): 1871-1879 (in Chinese with English abstract).
Jiang, S.H., Papaioannou, I., Straub, D., 2018. Bayesian Updating of Slope Reliability in Spatially Variable Soils with In-Situ Measurements. Engineering Geology, 239: 310-320. https://doi.org/10.1016/j.enggeo.2018.03.021
Jiang, S.H., Papaioannou, I., Straub, D., 2020. Optimization of Site-Exploration Programs for Slope-Reliability Assessment. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 6(1): 04020004. https://doi.org/10.1061/AJRUA6.0001042
Liu, G.X., Xi, J.C., Dai, E.F., et al., 2014. Loss Risk Assessment of the Hazard-Affectted Body of Landslides in China. Journal of Natural Disasters, 23(2): 39-46 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-ZRZH201402006.htm
Miotto, R., Wang, F., Wang, S., et al., 2018. Deep Learning for Healthcare: Review, Opportunities and Challenges. Briefings in Bioinformatics, 19(6): 1236-1246. doi: 10.1093/bib/bbx044
Papaioannou, I., Straub, D., 2017. Learning Soil Parameters and Updating Geotechnical Reliability Estimates Under Spatial Variability-Theory and Application to Shallow Foundations. Georisk, 11(1): 116-128. https://doi.org/10.1080/17499518.2016.1250280
Phoon, K.K., Kulhawy, F.H., 1999. Characterization of Geotechnical Variability. Canadian Geotechnical Journal, 36(4): 612-624. https://doi.org/10.1139/t99-038
Straub, D., 2014. Value of Information Analysis with Structural Reliability Methods. Structural Safety, 49: 75-85. https://doi.org/10.1016/j.strusafe.2013.08.006
Tang, Z.H., Chai, B., Liu, Z.C., et al., 2013. Reliability Analysis of Stability of Fill Slope. Earth Science, 38(3): 616-624 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQKX201303021.htm
Tang, Z.H., Yu, X.L., Chai, B., et al., 2021. Energetic Criterion of Entering Acceleration in Progressive Failure Process of Bedding Rockslide: A Case Study for Shanshucao Landslide. Earth Science, 46(11): 4033-4042 (in Chinese with English abstract).
Terbrugge, P.J., Wesseloo, J., Venter, J., et al., 2006. A Risk Consequence Approach to Open Pit Slope Design. Journal of the South African Institute of Mining and Metallurgy, 106(7): 503-511.
Wang, W., Chen, G. Q., Zhu, J., et al., 2018. Slope Stability Calculated with Strength Reduction Method Considering Tensile and Shear Progressive Failure. Chinese Journal of Rock Mechanics and Engineering, 37(9): 2064-2074 (in Chinese with English abstract).
Yang, R., Huang, J., Griffiths, D.V., et al., 2019. Optimal Geotechnical Site Investigations for Slope Design. Computers and Geotechnics, 114: 103111. https://doi.org/10.1016/j.compgeo.2019.103111
Yang, R., Huang, J., Griffiths, D.V., et al., 2021. Optimal Geotechnical Site Investigations for Slope Reliability Assessment Considering Measurement Errors. Engineering Geology, 297: 106497. http://www.sciencedirect.com/science/article/pii/S0013795221005081
Yoshida, I., Tasaki, Y., Otake, Y., et al., 2018. Optimal Sampling Placement in a Gaussian Random Field Based on Value of Information. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 4(3): 04018018. doi: 10.1061/AJRUA6.0000970
Zhang, J., Chen, H.Z., Huang, H.W., et al., 2015. Efficient Response Surface Method for Practical Geotechnical Reliability Analysis. Computers and Geotechnics, 69: 496-505. doi: 10.1016/j.compgeo.2015.06.010
Zhang, S., Tang, H.M., Liu, X., et al., 2018. Seepage and Instability Characteristics of Slope Based on Spatial Variation Structure of Saturated Hydraulic Conductivity. Earth Science, 43(2): 622-634 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQKX201802022.htm
Zhang, W.G., Wang, Q., Chen, F.Y., 2021. Reliability Analysis of Slope and Random Response of Anti-Sliding Pile Considering Spatial Variability of Rock Mass Properties. Rock and Soil Mechanics, 42(11): 3157-3168 (in Chinese with English abstract).
Zhao, J. X., Duan, L., Ma, J., et al., 2021. Importance Sampling for System Reliability Analysis of Soil Slopes Based on Shear Strength Reduction. Georisk, 15(4): 287-298. http://doc.paperpass.com/foreign/rgArti20207007479.html
Zhao, T., Wang, Y., 2020. Determination of Efficient Sampling Locations in Geotechnical Site Characterization Using Information Entropy and Bayesian Compressive Sampling. Canadian Geotechnical Journal, 56(11): 1622-1637. https://doi.org/10.1139/cgj-2018-0286
Zheng, Y.R., Zhao, S.Y., 2004. Application of Strength Reduction FEM in Soil and Rock Slope. Chinese Journal of Rock Mechanics and Engineering, 23(19): 3381-3388 (in Chinese with English abstract). doi: 10.3321/j.issn:1000-6915.2004.19.029
Zhou, Z., Li, D.Q., Xiao, T., et al., 2021. Response Surface Guided Adaptive Slope Reliability Analysis in Spatially Varying Soils. Computers and Geotechnics, 132: 103966. https://doi.org/10.1016/j.compgeo.2020.103966
傅方煜, 郑小瑶, 吕庆, 等, 2014. 基于响应面法的边坡稳定二阶可靠度分析. 岩土力学, 35(12): 3460-3466. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412016.htm
何成, 唐辉明, 申培武, 等, 2021. 应变软化边坡渐进破坏模式及稳定性可靠度. 地球科学, 46(2): 697-707. doi: 10.3799/dqkx.2020.058
蒋水华, 李典庆, 曹子君, 等, 2015. 考虑参数空间变异性的边坡可靠度及其敏感性分析多重响应面法. 防灾减灾工程学报, 35(5): 592-598. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201505007.htm
蒋水华, 刘贤, 尧睿智, 等, 2018. 基于贝叶斯更新和信息量分析的边坡钻孔布置方案优化设计方法. 岩土工程学报, 40(10): 1871-1879. doi: 10.11779/CJGE201810014
刘光旭, 席建超, 戴尔阜, 等, 2014. 中国滑坡灾害承灾体损失风险定量评估. 自然灾害学报, 23(2): 39-46. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201402006.htm
唐朝晖, 柴波, 刘忠臣, 等, 2013. 填土边坡稳定性的可靠度分析. 地球科学, 38(3): 616-624. doi: 10.3799/dqkx.2013.062
唐朝晖, 余小龙, 柴波, 等, 2021. 顺层岩质滑坡渐进破坏进入加速的能量学判据. 地球科学, 46(11): 4033-4042. doi: 10.3799/dqkx.2019.960
王伟, 陈国庆, 朱静, 等, 2018. 考虑张拉-剪切渐进破坏的边坡强度折减法研究. 岩石力学与工程学报, 37(9): 2064-2074. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201809006.htm
张抒, 唐辉明, 刘晓, 等, 2018. 基于饱和渗透系数空间变异结构的斜坡渗流及失稳特征. 地球科学, 43(2): 622-634. doi: 10.3799/dqkx.2017.617
仉文岗, 王琦, 陈福勇, 等, 2021. 考虑岩体空间变异性的边坡可靠度分析及抗滑桩随机响应研究. 岩土力学, 42(11): 3157-316. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202111024.htm
郑颖人, 赵尚毅, 2004. 有限元强度折减法在土坡与岩坡中的应用. 岩石力学与工程学报, 23(19): 3381-3388. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200419037.htm