Probabilistic Analysis of Large Slope Deformation Considering Soil Spatial Variability with Rotated Anisotropy
-
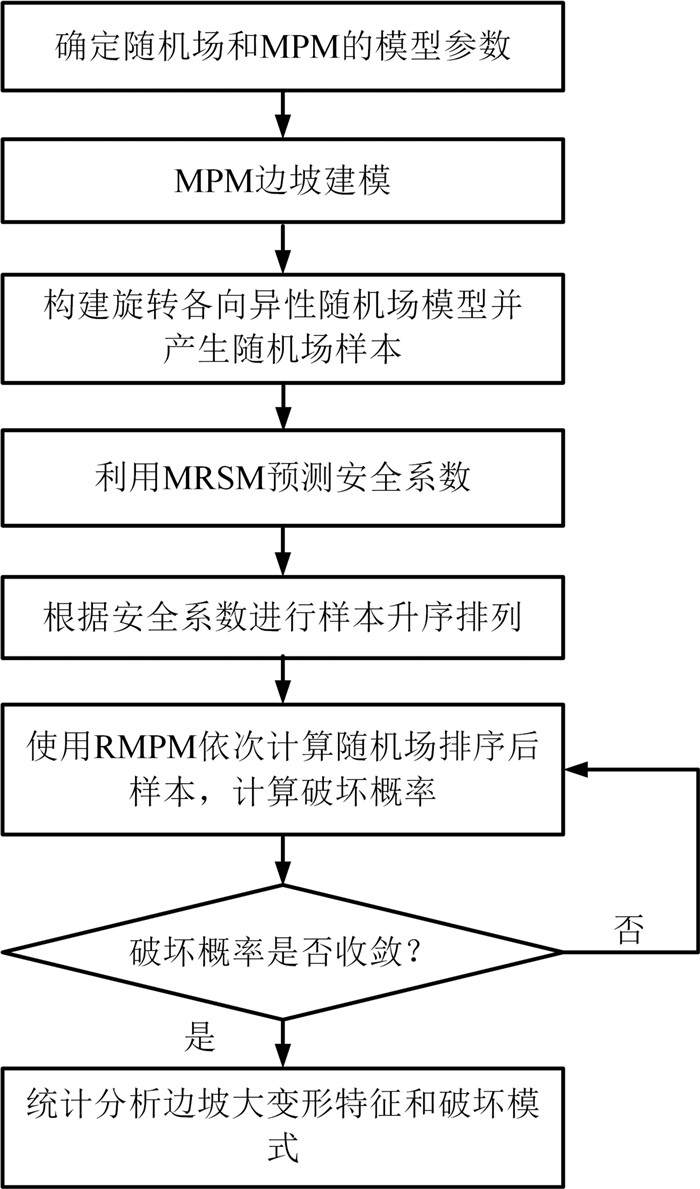
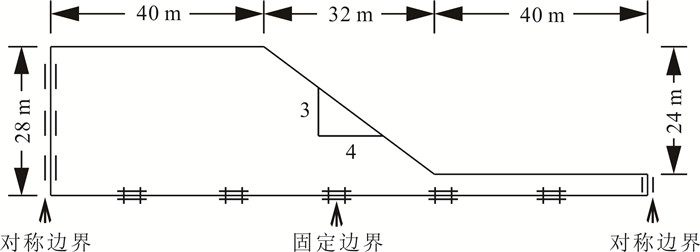
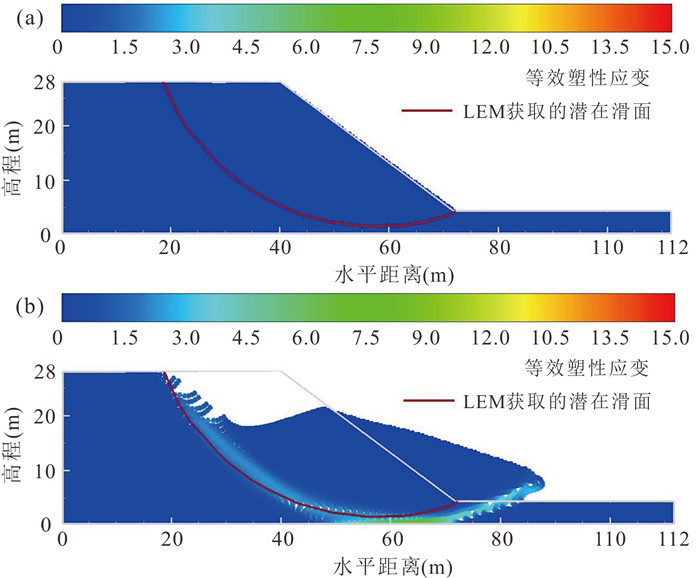
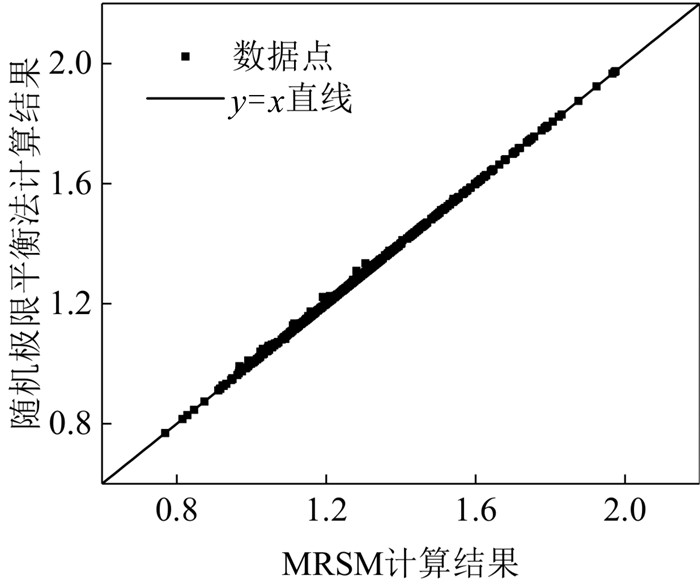
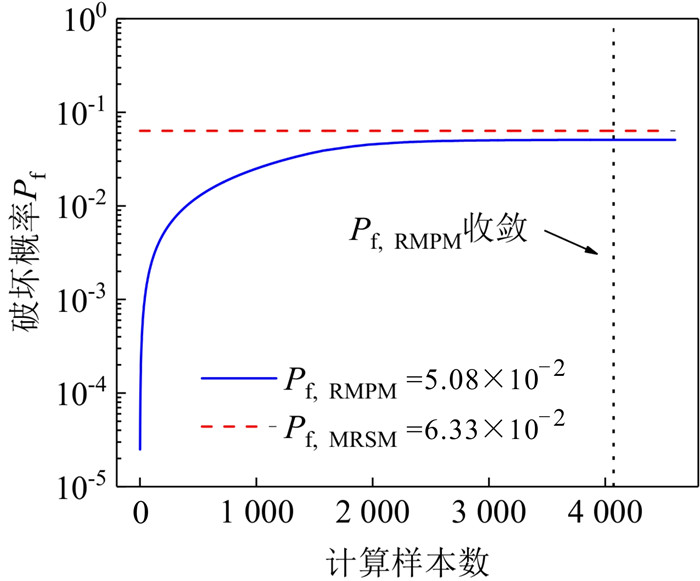
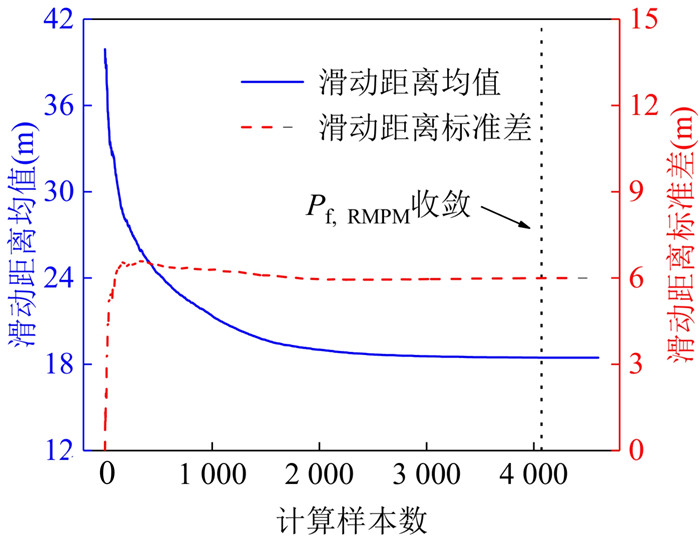
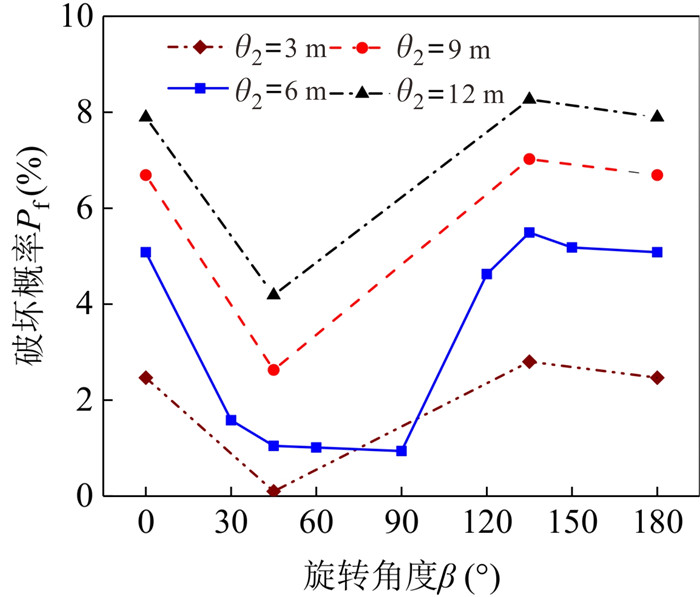
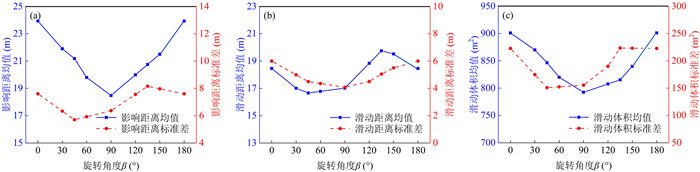
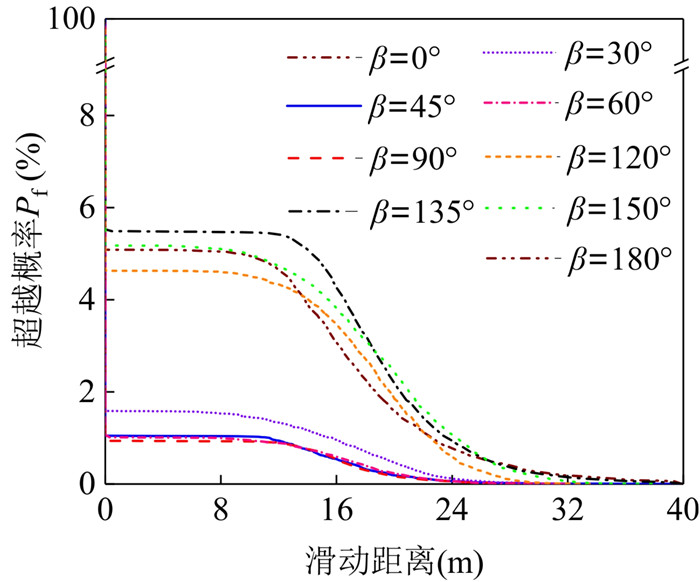
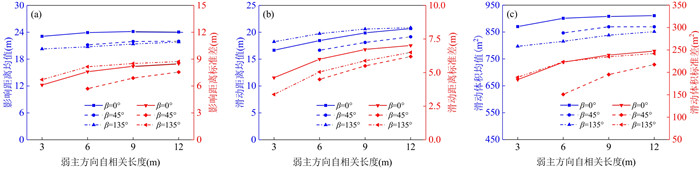
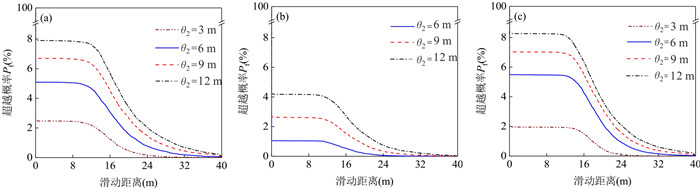
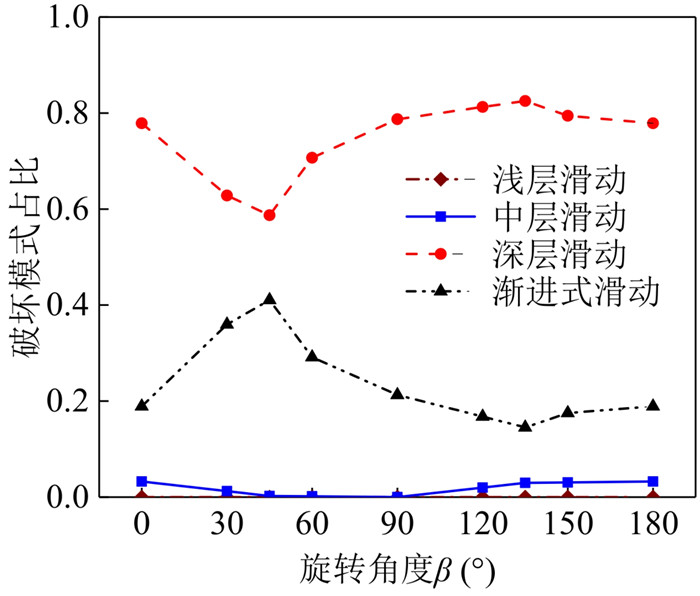
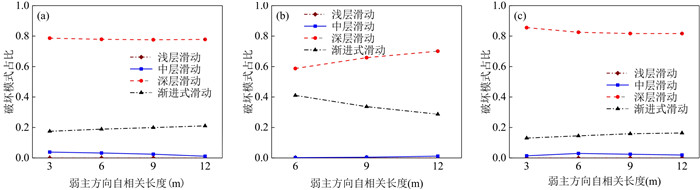
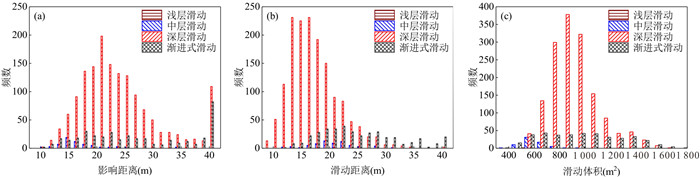
摘要: 为揭示土体参数旋转各向异性空间变异性对边坡大变形特征的影响规律，将土体不排水抗剪强度参数模拟为旋转各向异性随机场，提出采用多重响应面法对随机场样本进行边坡稳定性安全系数高效求解和升序排列，进而使用随机物质点法按序模拟随机场样本的边坡大变形过程.以一饱和不排水粘土边坡为例，研究了旋转各向异性随机场的旋转角度β和弱主方向自相关长度θ2对边坡大变形特征和破坏模式的影响.结果表明：提出的基于多重响应面的随机物质点方法可以高效开展边坡大变形概率分析；β和θ2对边坡大变形特征和破坏模式均有显著影响；边坡大变形破坏的影响距离、滑动距离和滑动体积的平均值与标准差均随θ2的增加而增加；边坡大变形过程中可能产生4种破坏模式，其中深层滑动和渐进式滑动为该边坡模型的主要概率失稳模式.因此，提出的方法为边坡大变形概率分析提供了一条有效途径，考虑参数旋转各向异性空间变异性的边坡大变形概率分析对准确评估边坡失稳风险具有一定的理论参考意义.Abstract: To explore the influence of spatial variability of soil parameters with rotated anisotropy on probabilistic large slope deformation characteristics, a multiple response surface-based random material point method is proposed in this study. First, random field theory is employed to simulate the spatial variability of soil parameters with rotated anisotropy. Then, the multiple response surface method is used to evaluate the factor of safety (FS) of each random field sample, based on which the FSs for all random field samples are sorted efficiently in an ascending order. Finally, the random material point method is used to sequentially simulate the large deformation features of a slope for the failed samples with the FS at less than 1. An undrained clay slope is taken as the illustrative example, where the undrained shear strength of the soil is simulated as a rotated anisotropic random field. The effect of the rotational angle β and the autocorrelation length θ2 in the minor principal direction of the rotated anisotropic random field on the large deformation features and failure modes of the slope are systematically studied. The results show that the proposed method can be efficiently conducted for probabilistic analysis of large slope deformation. Both β and θ2 have significant effects on large slope deformation features and failure modes. In terms of large deformation features, the mean and standard deviation of the influence distance, sliding distance, and sliding volume increase with the increase of θ2. There might be four failure modes when considering the rotated anisotropic spatial variability of the undrained strength of the slope, among which the deep sliding mechanism and progressive failure are the two main probabilistic failure modes. Therefore, the proposed method provides an effective way for the probabilistic large slope deformation analysis as well as a good theoretical reference for an accurate risk assessment of slope stability.
-
图 1 不同土体参数空间变异性现象
a.各向同性；b.横观各向异性；c.旋转各向异性；d.一般各向异性
Fig. 1. Practical phenomenon of soil spatial variability
图 2 不同空间变异性形式下随机场自相关系数三维曲面
a.各向同性随机场（θ1=1 m、θ2=1 m、β=0°）；b.横观各向异性随机场（θ1=5 m、θ2=1 m、β=0°）；c.旋转各向异性随机场（θ1=5 m、θ2=1 m、β=45°）
Fig. 2. Autocorrelation coefficient 3-D surfaces of random field under different forms of spatial variability
图 3 MPM计算流程示意
a.映射阶段；b.拉格朗日阶段；c.对流阶段
Fig. 3. Schematic diagram of material point method calculation flow
图 4 土体强度参数随机场属性值与物质点之间的映射方式
Fig. 4. The mapping mode between the random field properties and material points
图 5 随机多重响应面‒物质点法计算流程
Fig. 5. Flow chart of proposed random multiple response surface-material point method
图 8 物质点强度折减法确定性计算结果
a.折减系数为1.383；b.折减系数为1.384
Fig. 8. Deterministic slope stability analysis results by material point method with shear strength reduction method
图 10 MRSM和随机极限平衡法结果对比(R2=1)
Fig. 10. Comparison of multiple response surface method and random limit equilibrium method (R2=1)
图 12 滑动距离的均值和标准差收敛曲线
Fig. 12. Convergence curves of the mean and standard deviation of sliding distance
图 13 不同工况下的边坡破坏概率
Fig. 13. Probability of slope failure under different working conditions
图 14 边坡大变形特征统计值随旋转角度的变化曲线
a.影响距离；b.滑动距离；c.滑动体积
Fig. 14. Variations of statistics of slope large deformation features with rotational angle
图 15 不同旋转角度下滑动距离超越概率曲线
Fig. 15. Exceedance probability curves of sliding distance under different rotational angles
图 16 不同旋转角度下边坡大变形特征随弱主方向自相关长度的变化关系
a.影响距离；b.滑动距离；c.滑动体积
Fig. 16. Variations of statistics of large slope deformation features with the autocorrelation length in the minor principal direction under different rotational angles
图 17 不同弱主方向自相关长度下滑动距离超越概率曲线
a. β=0°; b. β=45°; c. β=135°
Fig. 17. Exceedance probability curves of sliding distance under different autocorrelation lengths in the minor principal direction
图 18 边坡破坏模式占比随旋转角度变化曲线
Fig. 18. Variations of proportion of slope failure modes with rotational angle
图 19 不同旋转角度下边坡破坏模式占比随弱主方向自相关长度的变化
a. β=0°; b. β=45°; c.β=135°
Fig. 19. Variations of proportion of slope failure modes with autocorrelation length in the minor principal direction under different rotational angles
图 20 不同破坏模式下边坡大变形特征分布直方图
a.影响距离；b.滑动距离；c.滑动体积
Fig. 20. Histograms of large slope deformation features under different failure modes
表 1 边坡土体参数
Table 1. Slope soil parameters
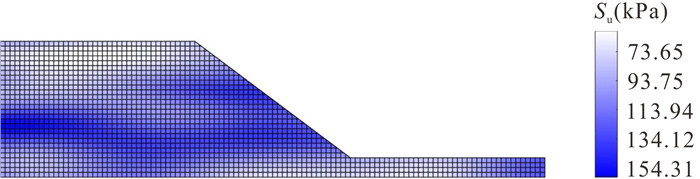
土体重度γ(kN·m-3) 弹性模量E(MPa) 泊松比$ \upsilon $ 不排水抗剪强度Su(kPa) 残余强度Su, res(kPa) 软化模量H(kPa) 19 100 0.3 100 0.5Su -50 
下载: 导出CSV
表 2 概率分析工况参数
Table 2. Parameters used for various probabilistic analysis cases
土体参数 均值(kPa) 变异系数 概率分布 随机场样本数 强主方向自相关长度θ1(m) 弱主方向自相关长度θ2(m) 旋转角度
β(°)不排水抗剪强度Su 100 0.3 对数正态随机场 40 000 24 3 0、45、135 6 0、30、45、60、90、120、135、180 9 0、45、135 12 0、45、135
下载: 导出CSV
表 3 不同破坏模式下边坡大变形特征统计值
Table 3. Statistics of large slope deformation features under different failure modes
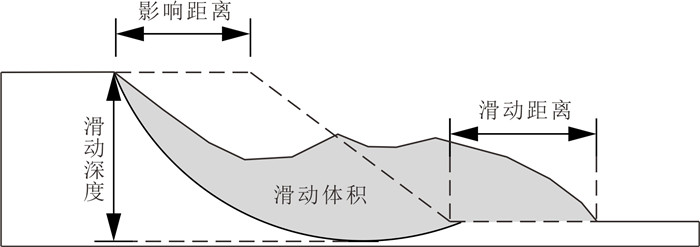
序号 破坏模式 均值 标准差 影响距离（m） 滑动距离（m） 滑动体积（m2） 影响距离（m） 滑动距离（m） 滑动体积（m2） 1 浅层滑动 ‒ ‒ ‒ ‒ ‒ ‒ 2 中层滑动 16.84 20.37 583.49 4.50 3.95 99.66 3 深层滑动 23.47 16.77 899.14 6.89 4.50 186.87 4 渐进式滑动 27.05 25.09 963.65 9.36 6.93 309.77
下载: 导出CSV
-
Andersen, S., Andersen, L., 2010. Modelling of Landslides with the Material-Point Method. Computational Geosciences, 14: 137-147. https://doi.org/10.1007/s10596-009-9137-y Augarde, C. E., Lee, S. J., Loukidis, D., 2021. Numerical Modelling of Large Deformation Problems in Geotechnical Engineering: A State-of-the-Art Review. Soils and Foundations, 61(6): 1718-1735. https://doi.org/10.1016/j.sandf.2021.08.007 Cami, B., Javankhoshdel, S., Phoon, K. K., et al., 2020. Scale of Fluctuation for Spatially Varying Soils: Estimation Methods and Values. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 6(4): 03120002. https://doi.org/10.1061/AJRUA6.0001083 Cheng, H. Z., Chen, J., Chen, R. P., et al., 2018. Risk Assessment of Slope Failure Considering the Variability in Soil Properties. Computers and Geotechnics, 103: 61-72. https://doi.org/10.1016/j.compgeo.2018.07.006 Cheng, H. Z., Chen, J., Wang, Z. S., et al., 2017. Stability Analysis of a Clay Slope Accounting for the Rotated Anisotropy Correlation Structure. Chinese Journal of Rock Mechanics and Engineering, 36(S2): 3965-3973 (in Chinese with English abstract). http://www.researchgate.net/publication/326149842_Stability_analysis_of_a_clay_slope_accounting_for_the_rotated_anisotropy_correlation_structure Cheng, H. L., Zhou, J. M., Chen, Z. Y., et al., 2021. A Comparative Study of the Seismic Performances and Failure Mechanisms of Slopes Using Dynamic Centrifuge Modeling. Journal of Earth Science, 32(5): 1166–1173. https://doi.org/10.1007/s12583-021-1481-4 Guo, Z. Z., Yin, K. L., Liu, Q. L., et al., 2020. Rainfall Warning of Creeping Landslide in Yunyang County of Three Gorges Reservoir Region Based on Displacement Ratio Model. Earth Science, 45(2): 672-684 (in Chinese with English abstract). He, C., Tang, H. M., Shen, P. W., et al., 2021. Progressive Failure Mode and Stability Reliability of Strain- Softening Slope. Earth Science, 46(2): 697-707 (in Chinese with English abstract). Hicks, M. A., Samy, K., 2002. Influence of Heterogeneity on Undrained Clay Slope Stability. Quarterly Journal of Engineering Geology and Hydrogeology, 35(1): 41-49. doi: 10.1144/qjegh.35.1.41 Huang, L., Cheng, Y. M., Leung, Y. F., et al., 2019. Influence of Rotated Anisotropy on Slope Reliability Evaluation Using Conditional Random Field. Computers and Geotechnics, 115: 103133. https://doi.org/10.1016/j.compgeo.2019.103133 Huang, L., Cheng, Y. M., Li, L., et al., 2021. Reliability and Failure Mechanism of a Slope with Non-Stationarity and Rotated Transverse Anisotropy in Undrained Soil Strength. Computers and Geotechnics, 132: 103970. https://doi.org/10.1016/j.compgeo.2020.103970 Jiang, S. H., Huang, J., Griffiths, D. V., et al., 2022. Advances in Reliability and Risk Analyses of Slopes in Spatially Variable Soils: A State-of-the-Art Review. Computers and Geotechnics, 141: 104498. https://doi.org/10.1016/j.compgeo.2021.104498 Jiang, S. H., Huang, J., Yao, C., et al., 2017. Quantitative Risk Assessment of Slope Failure in 2-D Spatially Variable Soils by Limit Equilibrium Method. Applied Mathematical Modelling, 47: 710-725. https://doi.org/10.1016/j.apm.2017.03.048 Jiang, X. P., Zhang, P., Lu, Y. W., et al., 2022. Slope Failure Criterion for the Strength Reduction Material Point Method. Bulletin of Geological Science and Technology, 41(2): 113-122 (in Chinese with English abstract). Li, D. Q., Jiang, S. H., Cao, Z. J., et al., 2015. A Multiple Response-Surface Method for Slope Reliability Analysis Considering Spatial Variability of Soil Properties. Engineering Geology, 187: 60-72. https://doi.org/10.1016/j.enggeo.2014.12.003 Li, D. Q., Xiao, T., Cao, Z. J., et al., 2016a. Enhancement of Random Finite Element Method in Reliability Analysis and Risk Assessment of Soil Slopes Using Subset Simulation. Landslides, 13: 293-303. https://doi.org/10.1007/s10346-015-0569-2 Li, D. Q., Xiao, T., Cao, Z. J., et al., 2016b. Efficient and Consistent Reliability Analysis of Soil Slope Stability Using Both Limit Equilibrium Analysis and Finite Element Analysis. Applied Mathematical Modelling, 40(9-10): 5216-5229. https://doi.org/10.1016/j.apm.2015.11.044 Li, D. Q., Zheng, D., Cao, Z. J., et al., 2016c. Response Surface Methods for Slope Reliability Analysis: Review and Comparison. Engineering Geology, 203: 3-14. https://doi.org/10.1016/j.enggeo.2015.09.003 Li, D. Q., Zheng, D., Cao, Z. J., et al., 2019. Two-Stage Dimension Reduction Method for Meta-Model Based Slope Reliability Analysis in Spatially Variable Soils. Structural Safety, 81: 101872. https://doi.org/10.1016/j.strusafe.2019.101872 Li, K., Cheng, Q. G., Lin, Q. W., et al., 2022. State of the Art on Rock Avalanche Dynamics from Granular Flow Mechanics. Earth Science, 47(3): 893-912 (in Chinese with English abstract). Lian, Y. P., Zhang, F., Liu, Y., et al., 2013. Material Point Method and Its Applications. Advances in Mechanics, 43(2): 237-264 (in Chinese with English abstract). Liu, X., Wang, Y., Li, D., 2019. Investigation of Slope Failure Mode Evolution during Large Deformation in Spatially Variable Soils by Random Limit Equilibrium and Material Point Methods. Computers and Geotechnics, 111: 301-312. https://doi.org/10.1016/j.compgeo.2019.03.022 Ma, G. T., Rezania, M., Nezhad, M. M., 2022. Uncertainty Quantification of Landslide Runout Motion Considering Soil Interdependent Anisotropy and Fabric Orientation. Landslides, 19 (2022): 1231-1247. https://doi.org/10.1007/s10346-021-01795-2 Mao, J., Liu, X., Zhang, C., et al., 2021. Runout Prediction and Deposit Characteristics Investigation by the Distance Potential-Based Siscrete Element Method: The 2018 Baige Landslides, Jinsha River, China. Landslides, 18: 235-249. https://doi.org/10.1007/s10346-020-01501-8 Nairn, J. A., 2013. Modeling Imperfect Interfaces in the Material Point Method Using Multimaterial Methods. CMES: Computer Modeling in Engineering & Sciences, 92(3): 271-299. http://pdfs.semanticscholar.org/c9af/6a640e932cc3f19a45aa470da54c60d653a1.pdf Ng, C. W., Qu, C., Cheung, R. W., et al., 2021. Risk Assessment of Soil Slope Failure Considering Copula-Based Rotated Anisotropy Random Fields. Computers and Geotechnics, 136: 104252. https://doi.org/10.1016/j.compgeo.2021.104252 Qu, C. X., Wang, G., Feng, K., et al., 2021. Large Deformation Analysis of Slope Failure Using Material Point Method with Cross-Correlated Random Fields (Cover Paper). Journal of Zhejiang University - Science A: Applied Physics & Engineering, 22: 856-869. https://doi.org/10.1631/jzus.A2100196 Sulsky, D., Chen, Z., Schreyer, H. L., 1994. A Particle Method for History-Dependent Materials. Computer Methods in Applied Mechanics and Engineering, 118(1-2): 179-196. doi: 10.1016/0045-7825(94)90112-0 Sun, X., Zeng, P., Li, T., et al., 2021. From Probabilistic Back Analyses to Probabilistic Run-out Predictions of Landslides: A Case Study of Heifangtai Terrace, Gansu Province, China. Engineering Geology, 280: 105950. https://doi.org/10.1016/j.enggeo.2020.105950 Wang, B., Hicks, M. A., Vardon, P. J., 2016. Slope Failure Analysis Using the Random Material Point Method. Geotechnique Letters, 6(2): 113-118. https://doi.org/10.1680/jgele.16.00019 Wang, L., Xu, F., Yang, Y., 2021. An Improved Total Lagrangian SPH Method for Modeling Solid Deformation and Damage. Engineering Analysis with Boundary Elements, 133: 286-302. https://doi.org/10.1016/j.enganabound.2021.09.010 Wang, S., Li, X. C., Shi, L., et al., 2016. Material Point Strength Reduction Method and Its Application to Slope Engineering. Rock and Soil Mechanics, 37(9): 2672-2678 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-YTLX201609033.htm Wang, Y., Cao, Z., Au, S. K., 2011. Practical Reliability Analysis of Slope Stability by Advanced Monte Carlo Simulations in a Spreadsheet. Canadian Geotechnical Journal, 48(1): 162-172. https://doi.org/10.1007/978-3-662-52914-0_7 Wang, Y., Qin, Z. W., Liu, X., et al., 2019. Probabilistic Analysis of Post-Failure Behavior of Soil Slopes Using Random Smoothed Particle Hydrodynamics. Engineering Geology, 261: 105266. https://doi.org/10.1016/j.enggeo.2019.105266 Wu, Y. P., Lu, L. E., Xue, Y., 2020. Application of Landslide Progressive Failure Mechanical Model Based on the Critical Stress State. Bulletin of Geological Science and Technology, 39(5): 1-7 (in Chinese with English abstract). Xiao, J H., Wang, M., Wang, C., et al., 2021. Reliability Analysis of Slope with Dominant Seepage Interlayer under Rainfall Infiltration. Bulletin of Geological Science and Technology, 40(6): 193-204 (in Chinese with English abstract). Xu, X., Yu, P., 2018. A Technique to Remove the Tensile Instability in Weakly Compressible SPH. Computational Mechanics, 62: 963-990. https://doi.org/10.1007/s00466-018-1542-4 Ying, C., Zhang, K., Wang, Z. N., et al., 2021. Analysis of the Run-out Processes of the Xinlu Village Landslide Using the Generalized Interpolation Material Point Method. Landslides, 18 (4): 1519-1529. https://doi.org/10.1007/s10346-020-01581-6 Zhang, S., Tang, H. M., Liu, X., et al., 2018. Seepage and Instability Characteristics of Slope Based on Spatial Variation Structure of Saturated Hydraulic Conductivity. Earth Science, 43(2): 622-634 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQKX201802022.htm Zhang, X., Chen, Z., Liu, Y., 2016. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases. Elsevier Inc., London, 165-190. Zhu, H., Zhang, L. M., 2013. Characterizing Geotechnical Anisotropic Spatial Variations Using Random Field Theory. Canadian Geotechnical Journal, 50 (7): 723-734. https://doi.org/10.1139/cgj-2012-0345 Zhu, H., Zhang, L. M., Xiao, T., 2019. Evaluating Stability of Anisotropically Deposited Soil Slopes. Canadian Geotechnical Journal, 56 (5): 753-760. https://doi.org/10.1139/cgj-2018-0210 程红战, 陈健, 王占盛, 等, 2017. 考虑旋转各向异性相关结构的黏土边坡稳定性分析. 岩石力学与工程学报, 36(S2): 3965-3973. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2029.htm 郭子正, 殷坤龙, 刘庆丽, 等, 2020. 基于位移比模型的三峡库区云阳县域内蠕变型滑坡降雨预警. 地球科学, 45(2): 672-684. doi: 10.3799/dqkx.2019.005 何成, 唐辉明, 申培武, 等, 2021. 应变软化边坡渐进破坏模式及稳定性可靠度. 地球科学, 46(2): 697-707. doi: 10.3799/dqkx.2020.058 蒋先平, 张鹏, 卢艺伟, 等, 2022. 物质点强度折减法边坡失稳判据选择方法. 地质科技通报, 41(2): 113-122. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202202011.htm 李坤, 程谦恭, 林棋文, 等, 2022. 高速远程滑坡颗粒流研究进展. 地球科学, 47(3): 893-912. doi: 10.3799/dqkx.2021.169 廉艳平, 张帆, 刘岩, 等, 2013. 物质点法的理论和应用. 力学进展, 43(2): 237-264. https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201302003.htm 王双, 李小春, 石露, 等, 2016. 物质点强度折减法及其在边坡中的应用. 岩土力学, 37(9): 2672-2678. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201609033.htm 吴益平, 卢里尔, 薛阳, 2020. 基于临界状态的边坡渐进破坏力学模型分析及应用. 地质科技通报, 39(5): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202005001.htm 肖景红, 王敏, 王川, 等, 2021. 含优势渗流层边坡降雨入渗下的可靠度分析. 地质科技通报, 40(6): 193-204. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202106021.htm 张抒, 唐辉明, 刘晓, 等, 2018. 基于饱和渗透系数空间变异结构的斜坡渗流及失稳特征. 地球科学, 43(2): 622-634. doi: 10.3799/dqkx.2017.617 -
点击查看大图
计量
- 文章访问数: 1157
- HTML全文浏览量: 476
- PDF下载量: 108
- 被引次数: 0
