Real-Time Discrimination Model for Local Earthquake Intensity Threshold Based on XGBoost
-
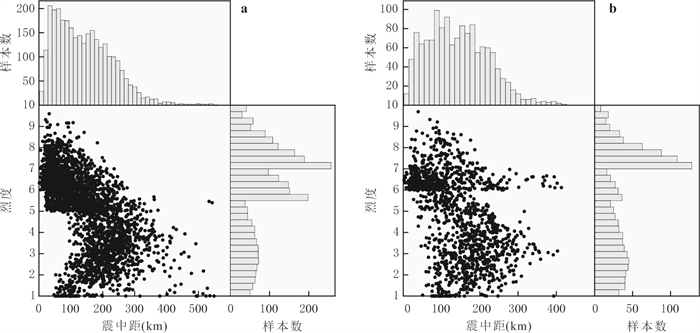
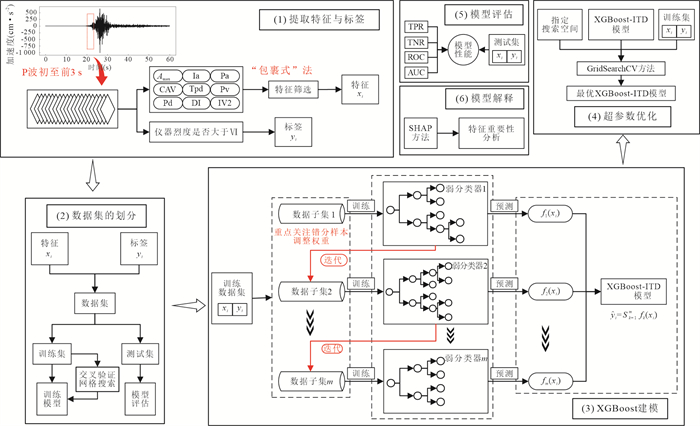
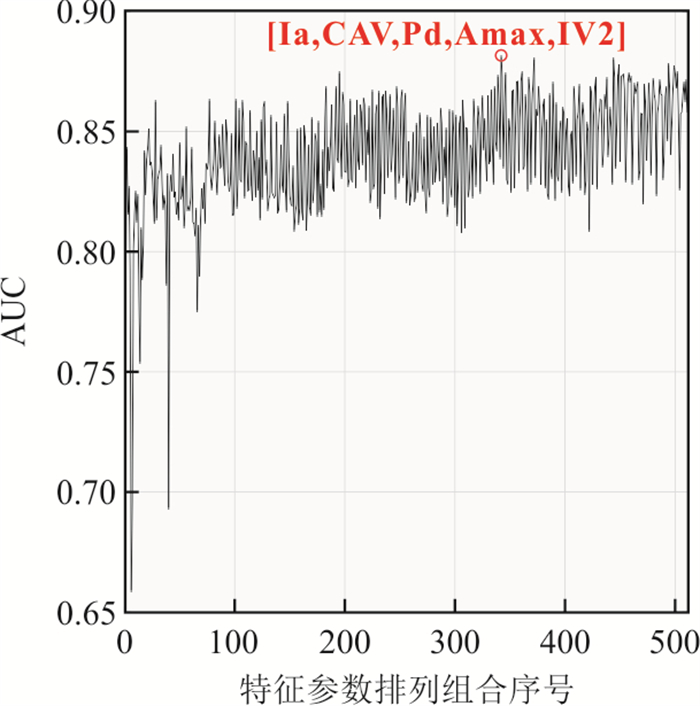
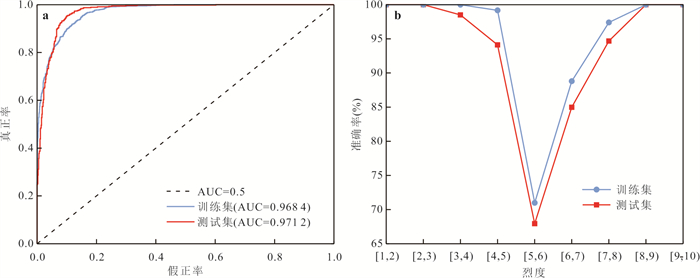
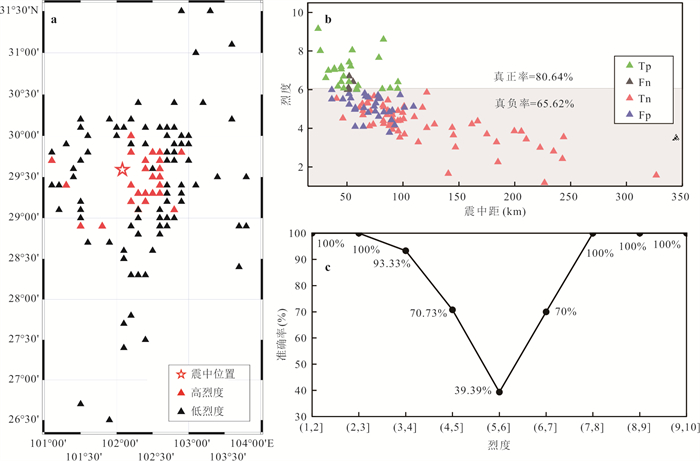
摘要: 如何在地震中利用台站接收到的少量P波信息预测该台站处的最终烈度是否会超越6度是地震预警研究中亟待解决的关键问题. 提出了一种基于极限梯度提升树（XGBoost）的现地烈度阈值实时判别模型，该模型以由台站接收到P波后3秒内的信息计算的5种特征作为输入参数，以该台站处的最终仪器地震烈度是否会超越6度作为阈值. 选取1996—2022年日本K-NET台网记录的460次地震的4 353条加速度记录建立了基于P波前3秒信息的烈度阈值实时判别模型（XGBoost-ITD）. 结果表明，该模型对低烈度的判别准确率为93%，对高烈度的判别准确率为88%. 在相同数据集条件下，相较于支持向量机分类方法及传统方法，XGBoost方法对现地烈度阈值判别具有更高的精度.Abstract: A key challenge in earthquake early warning (EEW) research is to predict whether the final intensity at a station during an earthquake will exceed 6 degrees using only a small amount of P-wave information received by the station. In this paper, we propose a real-time intensity threshold discrimination model based on Extreme Gradient Boosting Tree (XGBoost). The model uses five features calculated from the information within 3 seconds after receiving P-waves as input features, and uses the threshold of whether the final instrumental seismic intensity at the station will exceed 6 degrees. A total of 4 353 acceleration records from 460 earthquakes recorded by the Japanese K-NET seismic network from 1996 to 2022 were used to establish the XGBoost-based real-time intensity threshold discrimination model (XGBoost-ITD). The results indicate that the model's discrimination accuracy rate is 93% for low intensity and 88% for high intensity. Compared with the support vector machine classification method and the traditional method under the same dataset, the XGBoost method shows higher discrimination accuracy.
-
Key words:
- onsite warning /
- XGBoost /
- SHAP /
- machine learning /
- earthquake
-
图 1 选取记录的台站分布及震中分布图
a. 训练集台站分布；b. 测试集台站分布；c. 训练集震中分布；d. 测试集震中分布
Fig. 1. Distribution of selected recorded stations and earthquake epicenters
图 2 烈度与震中距分布图
a. 训练集；b. 测试集
Fig. 2. Distribution of intensity versus epicentral distance
图 4 不同参数组合下模型的AUC变化图
Fig. 4. The AUC score of the model under different parameter combinations
图 6 模型的评价图
a. ROC曲线及AUC值；b. 不同烈度样本的判别准确率
Fig. 6. Discriminant effect of the proposed model
图 7 各种模型的判别效果
a. ROC曲线及AUC值；b. 不同烈度样本的判别准确率
Fig. 7. Discriminant effect of various models
图 8 基于SHAP值的特征全局重要性排序图
Fig. 8. Feature global importance ranking chart based on SHAP value
图 9 (a) 震例的台站及震中位置分布; (b) XGBoost-ITD模型判别结果; (c) 不同烈度震例样本的判别准确率
Fig. 9. (a) Example distribution of stations and epicenter locations, (b) The discrimination results of XG Boost-ITD model, (c) discrimination accuracy of samples with different intensity
表 1 特征参数定义简介
Table 1. Definition of feature parameters
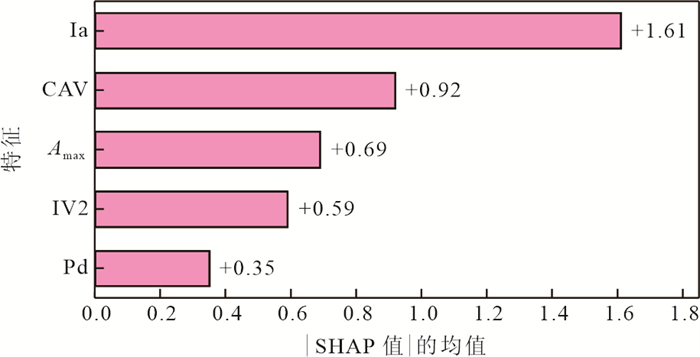
参数类型 特征名称 计算式 公式编号 (a)幅值参数 峰值加速度$ Pa $ $ Pa=\underset{{t}_{\mathrm{o}} < t < {t}_{\mathrm{o}}+3}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|a\right(t\left)\right| $ (4) 峰值速度$ Pv $ $ Pv=\underset{{t}_{\mathrm{o}} < t < {t}_{\mathrm{o}}+3}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|v\right(t\left)\right| $ (5) 峰值位移$ Pd $ $ Pd=\underset{{t}_{\mathrm{o}} < t < {t}_{\mathrm{o}}+3}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|d\right(t\left)\right| $ (6) (b)周期参数 最大卓越周期$ Tpd $
（详见Hildyard and Rietbrock, 2010）$ Tpd=\mathrm{m}\mathrm{a}\mathrm{x}\left(Tp{d}^{i}\right) $ (7) $ Tp{d}^{i}=2\mathrm{\pi }\sqrt{\frac{{X}_{i}}{{D}_{i}+{D}_{s}}} $ (8) (c)能量参数 累积绝对加速度$ CAV $ $ CAV={\int }_{{t}_{o}}^{{t}_{o}+3}\left|a\left(t\right)\right|\mathrm{d}t $ (9) Arias烈度$ Ia $ $ Ia=\frac{\mathrm{\pi }}{2g}{\int }_{{t}_{\mathrm{o}}}^{{t}_{\mathrm{o}}+3}{a}^{2}\left(t\right)\mathrm{d}t $ (10) 速度平方积分$ IV2 $ $ \mathrm{I}\mathrm{V}2={\int }_{{t}_{c}}^{{t}_{c}+3}{v}^{2}\left(t\right)\mathrm{d}t $ (11) (d)功率参数 破坏烈度$ DI $ $ DI=\mathrm{l}\mathrm{g}|a\cdot v| $ (12) (e)频谱参数 傅里叶谱幅值$ {A}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ $ F\left(\omega \right)=\mathcal{F}\left[a\left(t\right)\right] $ (13) $ {A}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{m}\mathrm{a}\mathrm{x}\left|F\left(\omega \right)\right| $ (14) 
下载: 导出CSV
表 2 模型的超参数调优细节
Table 2. Model hyperparameter optimization details
参数名称 说明 超参数取值范围 搜索步长 n-estimators 决策树的数量 [1, 300] 1 max-depth 树的最大深度 [1, 10] 1 min-child-weight 每个节点的最小权重和 [1, 10] 1 learning-rate 学习率 [0.01, 0.3] 0.05
下载: 导出CSV
表 3 混淆矩阵
Table 3. Confusion matrix
混淆矩阵 预测(负例)地震烈度$ < 6 $ 预测(正例)地震烈度$ \ge 6 $ 真实(负例)地震烈度$ < 6 $ $ {T}_{\mathrm{N}} $ $ {F}_{\mathrm{P}} $ 真实(正例)地震烈度$ \ge 6 $ $ {F}_{\mathrm{N}} $ $ {T}_{\mathrm{P}} $
下载: 导出CSV
表 4 模型评价指标的定义
Table 4. Definition of model evaluation index
评价指标 计算式 编号 精确率
(Precision)$ \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}=\frac{{T}_{\mathrm{P}}}{{T}_{\mathrm{P}}+{F}_{\mathrm{P}}} $ (18) 召回率/真正率
(Recall/TPR)$ \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}=\mathrm{T}\mathrm{P}\mathrm{R}=\frac{{T}_{\mathrm{P}}}{{T}_{\mathrm{P}}+{F}_{\mathrm{N}}} $ (19) F1得分
(F1score)$ \mathrm{F}1\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=\frac{2\times \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\times \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}} $ (20) 真负率(TNR) $ \mathrm{T}\mathrm{N}\mathrm{R}=\frac{{T}_{\mathrm{N}}}{{T}_{\mathrm{N}}+{F}_{\mathrm{P}}} $ (21) 假正率(FPR) $ \mathrm{F}\mathrm{P}\mathrm{R}=\frac{{F}_{\mathrm{P}}}{{T}_{\mathrm{N}}+{F}_{\mathrm{P}}} $ (22)
下载: 导出CSV
表 5 模型超参数取值表
Table 5. Table for model hyperparameters values
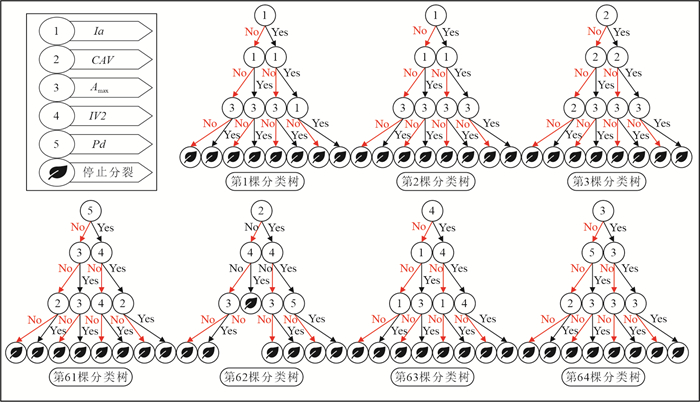
超参数名称 超参数取值 n-estimators 64 max-depth 3 min-child-weight 1 learning-rate 0.21
下载: 导出CSV
表 6 XGBoost-ITD模型评价指标表
Table 6. Evaluation result table of XGBoost-ITD model
数据集类型 精确率
(Precision)召回率/真正率
(Recall/TPR)F1得分
(F1score)真负率
(TNR)假正率
(FPR)训练集 0.836 1 0.913 8 0.873 2 0.884 2 0.115 8 测试集 0.902 8 0.877 0 0.889 7 0.934 3 0.065 7
下载: 导出CSV
表 7 各模型预测结果对比表
Table 7. Comparison of the prediction results of each model
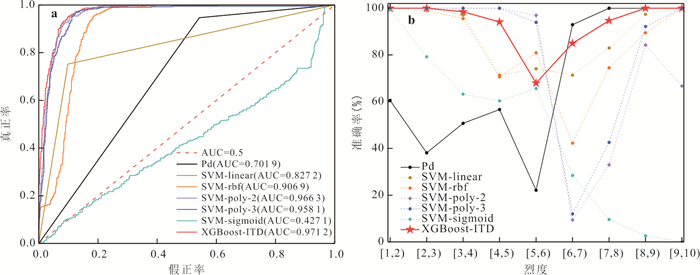
模型类型 精确率
(Precision)召回率/真正率
(Recall/TPR)F1得分
(F1score)真负率
(TNR)假正率
(FPR)Pd 0.548 0 0.946 5 0.694 1 0.457 2 0.542 8 SVM-linear 0.842 3 0.752 2 0.794 7 0.902 1 0.097 9 SVM-rbf 0.790 6 0.511 6 0.621 2 0.905 8 0.094 2 SVM-poly-2 0.963 3 0.187 2 0.313 4 0.995 0 0.005 0 SVM-poly-3 0.941 6 0.229 9 0.369 6 0.990 1 0.009 9 SVM-sigmoid 0.378 6 0.233 5 0.288 9 0.733 6 0.266 4 XGBoost-ITD 0.902 8 0.877 0 0.889 7 0.934 3 0.065 7
下载: 导出CSV
-
Allen, R. M., Gasparini, P., Kamigaichi, O., et al., 2009. The Status of Earthquake Early Warning around the World: An Introductory Overview. Seismological Research Letters, 80(5): 682-693. https://doi.org/10.1785/gssrl.80.5.682 Asselman, A., Khaldi, M., Aammou, S., 2021. Enhancing the Prediction of Student Performance Based on the Machine Learning XGBoost Algorithm. Interactive Learning Environments, 31(6): 3360-3379. https://doi.org/10.1080/10494820.2021.1928235 Böse, M., Felizardo, C., Heaton, T. H., 2015. Finite-Fault Rupture Detector (FinDer): Going Real-Time in Californian ShakeAlert Warning System. Seismological Research Letters, 86(6): 1692-1704. https://doi.org/10.1785/0220150154 Chen, T. Q., Guestrin, C., 2016. XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data, 785-794. https://doi.org/10.1145/2939672.2939785 Hildyard, M. W., Rietbrock, A., 2010. Tpd, a Damped Predominant Period Function with Improvements for Magnitude Estimation. Bulletin of the Seismological Society of America, 100(2): 684-698. https://doi.org/10.1785/0120080368 Hao, H. Z., Gu, Q., Hu, X. M., 2021. Research Advances and Prospective in Mineral Intelligent Identification Based on Machine Learning. Earth Science, 46(9): 3091-3106. (in Chinese with English abstract). Hu, J. J., Ding, Y. T., Zhang, H., et al., 2023. A Real-Time Seismic Intensity Prediction Model Based on Long Short-Term Memory Neural Network. Earth Science, 48(5): 1853-1864. (in Chinese with English abstract) Jin, X., Zhang, H. C., Li, J., et al., 2012. Research on Continuous Location Method Used in Earthquake Early Warning System. Chinese Journal of Geophysics, 55(3): 925-936. (in Chinese with English abstract) Jiang, B. G., Ma, Q., Tao, D. W., 2022. Continuous Estimation of Earthquake Early Warning Magnitude Based on Convolutional Neural Network. World Earthquake Engineering, 38(1): 213-228. (in Chinese with English abstract) Kanamori, H., 2005. Real-Time Seismology and Earthquake Damage Mitigation. Annual Review of Earth and Planetary Sciences, 33(1): 195-214. https://doi.org/10.1146/annurev.earth.33.092203.122626 Kanamori, H., 2015. Earthquake Hazard Mitigation and Real-Time Warnings of Tsunamis and Earthquakes. Pure and Applied Geophysics, 172(9): 2335-2341. https://doi.org/10.1007/s00024-014-0964-y Lundberg, S. M., Lee, S. I., 2017. A Unified Approach to Interpreting Model Predictions. Computer Science, 1-10. https://doi. org/https://doi.org/10.48550/arXiv.1705.07874. Lundberg, S. M., Erion, G. G., Lee, S. I., 2018. Consistent Individualized Feature Attribution for Tree Ensembles. Computer Science, 1-9. https://doi.org/10.48550/arXiv.1802.03888. Li, S. Y., 2018. Approaching the Earthquake Early Warning. Overview of Disaster Prevention, (2): 14-23. (in Chinese) Lu, J. Q., Li, S. Y., He, P. Y., et al., 2020. Energy- and Predominant-Period-Dependent P-Wave Onset Picker (EDP-Picker). Seismological Research Letters, 91(4): 2355-2367. https://doi.org/10.1785/0220190260 Li, S. Y., Wang. B. R., Lu J. Q., et al. 2023. Prediction of Instrumental Intensity for A Single Station Using A LSTM Neural Network. Chinese Journal of Geophysics(in Chinese with English abstract). Liu, L., Shen, J. K., Zhang, L. X., 2023. A Machine Learning-Based Method for Rapid Prediction of Earthquake Damage in Brick Masonry Houses. Earth Science, 48(5): 1769-1779. (in Chinese with English abstract). Ma, Q., 2008. Study and Application on Earthquake Early Warning (Dissertation). Institute of Engineering Mechanics China Earthquake Administration, Harbin(in Chinese with English abstract). Nielsen, D., 2016. Tree Boosting With XGBoost: Why Does XGBoost Win "Every" Machine Learning Competition? (Dissertation). Norwegian University of Science and Technology, Norway. Nicole, D. C., Tiziana, D. A., Claudio, D. S., et al., 2023. Comparing Filter and Wrapper Approaches for Feature Selection in Handwritten Character Recognition, Pattern Recognition Letters, 168(5): 39-46. https://doi.org/10.1016/j.patrec.2023.02.028 Peng, C. Y., Yang, J. S., Zheng, Y., et al., 2017. New τc Regression Relationship Derived from all P Wave Time Windows for Rapid Magnitude Estimation. Geophysical Research Letters, 44(4): 1724-1731. https://doi.org/10.1002/2016gl071672 Satriano, C., Lomax, A., Zollo, A., 2008. Real-Time Evolutionary Earthquake Location for Seismic Early Warning. Bulletin of the Seismological Society of America, 98(3): 1482-1494. https://doi.org/10.1785/0120060159 State Administration for Market Regulation, Standardization Administration of China., 2020. GB/T-17742-2020, The Chinese seismic intensity scale. China Quality and Standards Publishing & Media Co., Ltd, Beijing (in Chinese) Song, J. D., Yu, C., Li, S. Y., 2022. Continuous Prediction of Onsite PGV for Earthquake Early Warning Based on Least Squares Support Vector Machine. Chinese Journal of Geophysics, 64(2): 555-568. (in Chinese with English abstract) Wu, Y. M., Kanamori, H., 2005. Rapid Assessment of Damage Potential of Earthquakes in Taiwan from the Beginning of P Waves. Bulletin of the Seismological Society of America, 95(3): 1181-1185. https://doi.org/10.1785/0120040193 Wu, Y. M., Kanamori, H., 2008. Development of an Earthquake Early Warning System Using Real-Time Strong Motion Signals. Sensors, 8(1): 1-9. https://doi.org/10.3390/s8010001 Wen, Z. Y., He, B. S., Kotagiri, R., et al., 2018. Efficient Gradient Boosted Decision Tree Training on GPUs. 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS). 234-243. https://doi.org/10.1109/IPDPS40821.2018 Wang, A., Li, S. Y., Lu, J. Q., et al., 2023. Prediction of PGA in Earthquake Early Warning Using a Long Short-Term Memory Neural Network. Geophysical Journal International, 234(1): 12-24. https://doi.org/10.1093/gji/ggad067 Wang, M., Yang, J. L., Wang, X., et al., 2023. Identification of Shale Lithofacies by Well Logs Based on Random Forest Algorithm. Earth Science, 48(1): 130-142. (in Chinese with English abstract). Yamada, M., Heaton, T., Beck, J., 2007. Real-Time Estimation of Fault Rupture Extent Using Near-Source Versus Far-Source Classification. Bulletin of the Seismological Society of America, 97(6): 1890-1910. https://doi.org/10.1785/0120060243 Yu, C., Song, J. D., Li, S. Y., 2021. Prediction of Peak Ground Motion for On-Site Earthquake Early Warning Based on SVM. Journal of Vibration and Shock, 40(3): 63-72. (in Chinese with English abstract). 国家市场监督管理总局, 国家标准化管理委员会, 2020. GB/T-17742-2020, 中国地震烈度表. 北京: 中国标准出版社. 郝慧珍, 顾庆, 胡修棉, 2021. 基于机器学习的矿物智能识别方法研究进展与展望. 地球科学, 46(9): 3091-3106. doi: 10.3799/dqkx.2020.360 胡进军, 丁祎天, 张辉, 等, 2023. 基于长短期记忆神经网络的实时地震烈度预测模型. 地球科学, 48(5): 1853-1864. doi: 10.3799/dqkx.2022.338 金星, 张红才, 李军, 等, 2012. 地震预警连续定位方法研究. 地球物理学报, 55(3): 925-936. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201203021.htm 江炳根, 马强, 陶冬旺, 2022. 基于卷积神经网络的地震预警震级持续估算方法研究. 世界地震工程, 38(1): 213-228. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC202201022.htm 李山有, 2018. 走近地震预警. 防灾博览, (2): 14-23. https://www.cnki.com.cn/Article/CJFDTOTAL-FZBL201802010.htm 李山有, 王博睿, 卢建旗等, 2023. 基于LSTM网络的单台仪器地震烈度预测模型. 地球物理学报. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX202402012.htm 刘丽, 沈俊凯, 张令心, 2023. 基于机器学习的砖砌体房屋震害快速预测方法. 地球科学, 48(5): 1769-1779. doi: 10.3799/dqkx.2022.481 马强, 2008. 地震预警技术研究及应用(博士学位论文). 哈尔滨: 中国地震局工程力学研究所. 宋晋东, 余聪, 李山有, 2021. 地震预警现地PGV连续预测的最小二乘支持向量机模型. 地球物理学报, 64(2): 555-568. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX202102014.htm 王民, 杨金路, 王鑫, 等. 2023. 基于随机森林算法的泥页岩岩相测井识别. 地球科学, 48(1): 130-142. doi: 10.3799/dqkx.2022.181 余聪, 宋晋东, 李山有, 2021. 基于支持向量机的现地地震预警地震动峰值预测. 振动与冲击, 40(3): 63-72. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202103010.htm -
点击查看大图
计量
- 文章访问数: 945
- HTML全文浏览量: 533
- PDF下载量: 144
- 被引次数: 0
