Simulations of Random Medium Model and Intermixed Random Medium
-
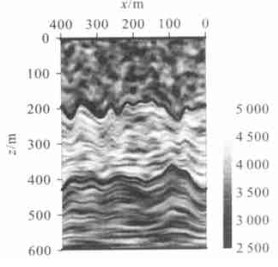
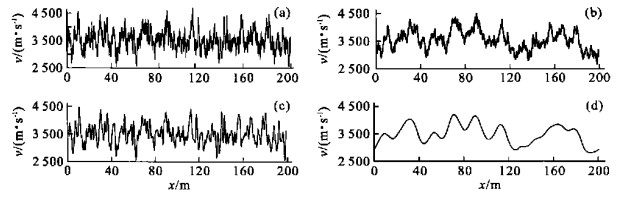
摘要: 讨论了随机介质模型的基本概念及指数型和高斯型椭圆自相关函数所描述的随机介质模型的特点, 并提出了混合型随机介质模型的概念, 该随机介质模型能更加灵活、准确地描述实际介质.通过选择在水平方向和垂直方向上的自相关长度a、b以及粗糙度r, 可以产生出各种不同形式的混合型随机介质模型.模拟结果显示, 混合型随机介质模型能更加灵活地描述实际介质, 具有适应性强, 使用方便、灵活, 能有效地模拟油气藏细节的优点.Abstract: We discussed some basic concept of random media, and discussed the characteristics of random media models with exponential and Gaussian elliptic autocorrelation functions. Meanwhile by integrating the characteristics of random media models with exponential and Gaussian elliptic autocorrelation functions, we put forward the concept of roughness factor, and hereafter the concept of intermixed random medium model, which may describe the realistic media more agilely and precisely. By selecting the autocorrelation length a of horizontal direction, b of vertical direction and r of roughness factor, we may generate diversified intermixed random media models. The results of simulations show that the intermixed random media model can describe the realistic media more agilely, with strong adaptability and convenience and agile use, and thus can simulate details of the reservoir efficiently.
-
-
[1] Ikelle L T, Yung S K, Daube F. 2-D random media with ellipsoidal autocorrelation function[J]. Geophysics, 1993, 58(9): 1359-1372. doi: 10.1190/1.1443518 [2] Ergintav S, Canitez N. Modeling of multi-scale media in discrete form[J]. Journal of Seismic Exploration, 1997, 6: 77-96. [3] Dainty A M. High-frequency acoustic backscattering and seismic attenuation[J]. J Geophys Res, 1984, 89: 3172-3176. doi: 10.1029/JB089iB05p03172 [4] Frankel A, Clayton R. Finite difference simulations of seismic scattering: implications for the propagation of short-period seismic waves in the crust and models of crustal heterogeneity[J]. J Geophys Res, 1986, 91: 6465-6489. doi: 10.1029/JB091iB06p06465 [5] Charratte E. Elastic wave scattering in laterally inhomogeneous media[D]. Cambridge, M A: Massachusetts Institute of Technology, 1991. [6] Jannaud L R, Adler P M, Jacqin C G. Spectral analysis and inversion of codas[J]. J Geophys Res, 1991, 96 (b): 18215-18231. [7] Kerner C. Anisotropy in sedimentary rocks modeled as random media[J]. Geophysics, 1992, 57: 564-576. doi: 10.1190/1.1443270 [8] Korn M. Seismic wave in random media[J]. J Applied Geophys, 1993, 29: 247-269. doi: 10.1016/0926-9851(93)90007-L [9] Hestholm S O, Huseybe E S, Ruud B O. Seismic wave propagation in complex crust-upper mantel media using finite-difference synthetics[J]. Geophys J Int, 1994, 118: 643-670. doi: 10.1111/j.1365-246X.1994.tb03991.x [10] Flatte' S M, Wu R S. Small-scale structure in the lithosphere and asthenosphere deduced from arrival time and amplitude fluctuations at NORSAR[J]. J Geophys Res, 1988, 93: 6601-6614. doi: 10.1029/JB093iB06p06601 [11] Roth M, Korn M. Single-scattering theory versus numerical modeling in two-dimensional random media[J]. Geophys J Int, 1993, 112: 124-140. doi: 10.1111/j.1365-246X.1993.tb01442.x -










 下载:
下载: