非线性矿床模型与非常规矿产资源评价

成秋明

非线性矿床模型与非常规矿产资源评价

成秋明^{1, 2,}

1.
中国地质大学地球系统和矿产资源工程实验室, 湖北武汉 430074
2.
York 大学地球大气系, 加拿大多伦多 M3J1P3

基金项目:

加拿大自然科学基金“研究和开发矿产资源和环境评价GIS空间分析和多重分形方法和系统”项目 NSERC-OGP0183993

详细信息

作者简介:
成秋明（1960-）, 男, 教授, 1994年毕业于加拿大渥太华大学, 获博士学位, 现为中国地质大学教育部长江学者特聘教授, 加拿大York大学教授, 主要从事矿产与勘探、数学地质、地理信息系统、矿产资源与环境评价的教学和研究.E-mail: qiuming@yorku.ca

中图分类号: P628
计量
- 文章访问数: 3806
- HTML全文浏览量: 688
- PDF下载量: 24
- 被引次数: 0
出版历程
- 收稿日期: 2003-04-21
- 刊出日期: 2003-07-25

Non-Linear Mineralization Model and Information Processing Methods for Prediction of Unconventional Mineral Resources

CHENG Qiu-ming^{1, 2
,}

1.
L aboratory of Earth Systems and Mineral Resources Engineering, China University of Geosciences, Wuhan 430074, China
2.
Department of Earth and Atmospheric Science, York University, Toronto, Canada M3J1P3

摘要

摘要: 探讨了建立非线性矿床模型对难识别的非常规矿产资源评价的可能性.首先评述了非线性理论在成矿动力学和矿产勘查中的应用, 以及非常规矿床与非常规矿产资源评价的研究现状.然后引进了以岩浆结晶分异成矿作用为例的多维分形非线性成矿系统模型.在此基础上揭示了非线性成矿系统必然导致元素富集和聚集的奇异分布及矿床分布的广义自相似性规律.广义自相似性刻画了成矿的外在多样性和内在相似性.介绍了2种最新研究的“奇异分析”和“广义自相似性”异常分解方法.采用文中所建议的非线性矿床模型方法对加拿大北部Gowganda地区的热液型Co, Ni, Ag, As, Pb 5种元素矿产进行了预测和评价.结果表明, 以“广义自相似性”和“奇异分析”为基础的非线性矿床模型及GIS信息综合技术对非常规难识别矿产资源评价是有效的.
- 非线性矿床模型 /
- 广义自相似性理论 /
- 奇异分析方法 /
- 成矿系数 /
- GIS信息综合
Abstract: A non-linear mineralization model was proposed on the basis of a classical igneous differentiation mineralization model which can describe the generation of multi-fractal distribution of element concentration as well as grade-tonnage fractal/multi-fractal model. The work has also led to a model to explain the common properties of mineralization and mineralization-associated geochemical anomaly diversity and generalized self-similarity of the anomalies. Generalized self-similarity is related to the generalized scaling invariance which can characterize the external diversity and internal similarity of natural phenomena including mineralization and occurrence of mineral deposits. The models based on core principal of generalized self-similarity and singularity analysis have been applied to a case study of Co-Ni-Ag-As-Pb mineral resources assessment in the Gowganda area of Abitibi district, northern Ontario, Canada. The results have demonstrated that the non-linear models proposed in the current research are effective for delineating week lake sediment and water geochemical anomalies caused by deeply buried sources or week anomalies superimposed to low background values.
- non-linear mineralization model /
- generalized self-similarity /
- singularity analysis method /
- mineralization index /
- GIS data integration

HTML全文

图 1 研究区地质简图

较浅的点图案反映的是元古代Lorrain组石英砂岩、粉砂岩、角砾岩及Gowganda组泥质变质岩地层; 较大的点图案反映的是太古代酸性到基性超基性火山变质岩地层; 灰色带状的图案反映的是切割侵入太古代和元古代变质岩的后期Nipissing辉绿岩脉; 三角符号表示Co, Ni, As, Ag, Pb 5种元素矿床和矿点分布

Fig. 1. Simplified geology map

下载: 全尺寸图片幻灯片

图 2 湖泊沉积物地球化学取样^[26]

Fig. 2. Fig.2 Location map of 1 172 lake sediment samples^[26]

下载: 全尺寸图片幻灯片

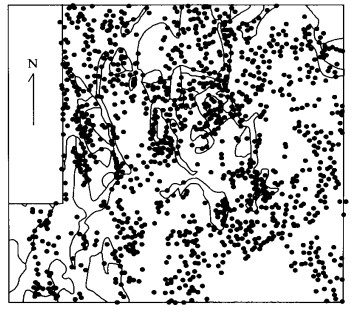
图 3 湖泊沉积物Ag地球化学(a) 及奇异指数分布(b)

采用GeoDAS GIS软件多维分形插值方法^[28].网格大小为150 m, 图像大小387×404, 窗口内最少12个样品, 查寻半径为1 500 m; a.正规化后的Ag数值.三角符号表示Co, Ni, As, Ag, Pb 5种元素矿床和矿点分布; b.图中灰度表示α < 2的程度.三角符号表示Co, Ni, As, Ag, Pb 5种元素矿床和矿点分布

Fig. 3. Ag values (a) and singularity (b) in lake sediment samples

下载: 全尺寸图片幻灯片

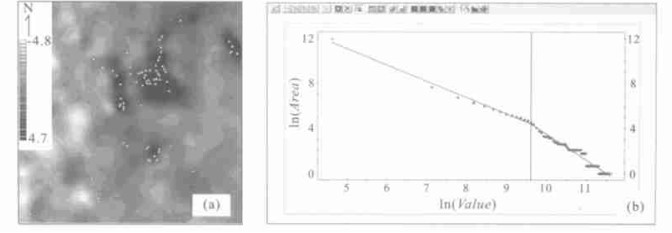
图 4 第三因子得分(a) 及其对应的S-A关系(b)

a.采用GeoDAS GIS软件中网格化数据主成分分析方法^[25].组成该因子的主要元素包括Cu, Pb, Co, Ag等.图中灰度表示因子得分.三角符号表示Co, Ni, As, Ag, Pb 5种元素矿床和矿点分布; b.采用GeoDAS GIS软件中S-A分形方法^[28].横坐标表示ln能谱密度S, 纵坐标表示ln面积A (≥S).阀值ln S=9.6将能谱密度分为2组具有不同广义自相似性的范围.这2个不同的分布范围将形成不同的滤波器: 小于ln S=9.6的范围为异常滤波器, 大于ln S=9.6的范围为背景滤波器.采用逆傅立叶变换并利用这两种滤波器可将第三因子得分图分解, 结果见图 5

Fig. 4. Scores on the third PCA contributed mainly (a) and power-law relationships between power spectrum energy density Sand the area A (≥S) on frequency domain (b)

下载: 全尺寸图片幻灯片

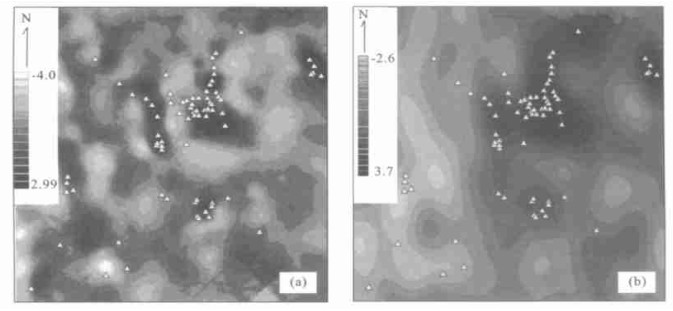
图 5 采用S-A方法和图 4b中给出的异常滤波器得到的第三因子组合异常(a) 及背景(b)

图中灰度表示异常相对强度.三角符号表示Co, Ni, As, Ag, Pb 5种元素矿床和矿点分布

Fig. 5. Anomaly (a) and background (b) map calculated using S-A method with the anomaly filter defined in

下载: 全尺寸图片幻灯片

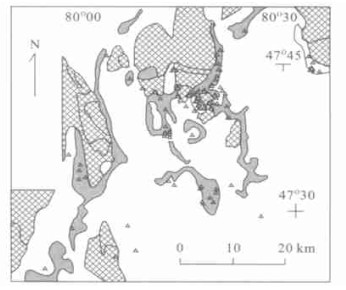
图 6 矿床分布潜力后验概率

采用GeoDAS GIS模糊证据权方法, 综合了第三主因子异常、航磁异常、航空放射性异常及重力异常等信息层^[27].图中灰度表示后验概率.三角符号表示Co, Ni, As, Ag, Pb 5种元素已知矿床和矿点分布

Fig. 6. Posterior probability for potential occurrence of mineral deposits of five-element type

下载: 全尺寸图片幻灯片

参考文献(28)

[1]	赵鹏大. 地质异常与成矿预测: 当代矿产资源勘查评价的理论与方法[M]. 北京: 地质出版社, 1998. ZHAO P D. Geological anomaly and mineral prediction: current mineral resources assessment theory and method [M]. Beijing: Geological Publishing House, 1998.
[2]	赵鹏大. 地球科学的新使命——认知和发现非传统矿产资源[J]. 地球物理学进展, 2001, 16(4): 127-132. doi: 10.3969/j.issn.1004-2903.2001.04.016 ZHAO P D. Task of the earth sciences: identify and discover untraditional mineral resources[J]. Progress in Geophysics, 2001, 16(4): 127-132. doi: 10.3969/j.issn.1004-2903.2001.04.016
[3]	Heroy W B. Unconventional methods in exploration for petroleum and natural gas[D]. Dallas: Southern Methodist University, 1969.218.
[4]	Shanks W C Ⅲ. Cameron volume on unconventional mineral deposits[M]. New York: Am Inst Min Metall and Pet Eng Soc Min Eng, 1983.246.
[5]	Barton P B. Unconventional mineral deposits: a challenge to geochemistry[A]. In: Shanks W C Ⅲ, ed. Cameron volume on unconventional mineral deposits[C]. New York: Am Inst Min Metall and Pet Eng Soc Min Eng, 1983.3-14.
[6]	Tooker E W. Unconventional future ores[A]. In: Brown M, ed. Encyclopaediaof materialssciences and engineering [C]. New York: Pergamon Press, 1982.
[7]	Van Rensburg W C J. Global economics relating to the exploration of unconventional mineral resources[A]. In: Shanks W C Ⅲ, ed. Cameron volume on unconventional mineral deposits[C]. New York: Am Inst Min Metall and Pet Eng Soc Min Eng, 1983.15-20.
[8]	Wilde A, Edwards A, Yakubchuk A. Unconventional deposits of Pt and Pd: a review with implications for exploration[J]. Newsletter SEG, 2003, 52: 10-18.
[9]	Turcotte D L. Fractals in petrology[J]. Lithos, 2002, 65: 261-271. doi: 10.1016/S0024-4937(02)00194-9
[10]	Cheng Q, Agterberg F P, BallantyneS B. Theseparation of geochemical anomalies from background by fractal methods[J]. Journal of Exploration Geochemistry, 1994, 51 (2): 109-130. doi: 10.1016/0375-6742(94)90013-2
[11]	Agterberg F P. Power-law versus lognormal models in mineral exploration[A]. In: Mitri H S, ed. Proceedings of the third Canadian conference on computer applications in the mineral industry[C]. Moutreal: McGill University, 1995.17-26.
[12]	於崇文. 地球系统的复杂性——地球科学的基本问题(Ⅰ)[J]. 地球科学——中国地质大学学报, 2002, 27 (5): 509-519. YU C W. Complexity of earth systems-fundamental issues of earth sciences (Ⅰ)[J]. Earth Science-Journal of China University of Geosciences, 2002, 27(5): 509- 519.
[13]	Zhang Z, Ma H, Cheng Q. Fractal geometry of element distribution on mineral surfaces[J]. Math Geol, 2001, 33: 217-228. doi: 10.1023/A:1007587318807
[14]	Cheng Q. GIS-based fractal anomaly analysis for prediction of mineralization and mineral deposits[A]. In: Harris J, ed. GIS applications in the earth sciences[C]. [s. l. ]: Geological Association of Canada, 2003.
[15]	Zhao P D, Chen Y Q. Geo-anomaly: extreme value distribution in geology and its applications in quantitative assessment of mineral resources[J]. Bulletin of the Int Stat Inst, 2001, 53: 477-480.
[16]	Cheng Q. Decomposition of geochemical map patterns using scaling properties to separate anomalies from background[J]. Bulletin of the Int Stat Inst, 2001, 53: 481 -484.
[17]	Cheng Q. A new model for quantification of anisotropic scale invariance and for anomaly decomposition[J]. Math Geol, 2003 (in Press).
[18]	Turcotte D L. Fractals and chaos in geology and geophysics[M]. 2nd ed. Cambridge: Cambridge University Press, 1997.398.
[19]	Cheng Q. Multifractality and spatial statistics[J]. Computers&Geosciences, 1999, 25(9): 949-961.
[20]	赵鹏大. "三联式"资源定量预测与评价——数字找矿理论与实践探讨[J]. 地球科学——中国地质大学学报, 2002, 27(5): 482-489. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200205001.htm ZHAO P D. "Three components"mineral resources quantitative assessment-digital prospecting theory and practice[J]. Earth Science-Journal of China University of Geosciences, 2002, 27(5): 482-489. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200205001.htm
[21]	赵鹏大, 陈建平, 陈建国. 成矿多样性与成矿谱系[J]. 地球科学——中国地质大学学报, 2001, 26 (2): 111-117. https://cdmd.cnki.com.cn/Article/CDMD-10491-1013354295.htm ZHAO P D, CHEN J P, CHEN J G. Mineral diversity and mineralization spectrum[J]. Earth Science-Journal of China University of Geosciences, 2001, 26(2): 111- 117. https://cdmd.cnki.com.cn/Article/CDMD-10491-1013354295.htm
[22]	Cheng Q. A new technique for quantification of anisotropic scale invariance and for decomposition of mixing patterns[A]. In: Bayer U, Burger H, Skala W, eds. Proceedings of the8th annual conference of the international association for mathematical geology[C]. Berlin: Free University, 2002.359-364.
[23]	Cheng Q, Xu Y, Grunsky E. Multifractal power spectrum-area method for geochemical anomaly separation [J]. Natural Resources Research, 2000, 9(1): 43-51. doi: 10.1023/A:1010109829861
[24]	Schertzer D, Lovejoy S. Nonlinear variability in geophysics[M]. Dordrecht: Kluwer Academic Publ, 1991. 318.
[25]	Panahi A, Cheng Q, Bonham-Carter G F. Modeling lake sediment geochemical distribution using spatial principal component, indicator kriging and mult-i fractal powerspectrum analysis: a case study from Gowganda, Ontario [J]. Journal of Geochemistry: Exploration, Environment and Analysis, 2003 (in Press).
[26]	Hamilton S M. A high density lake sediment and water geochemical survey of 32 geographic townships in the Montreal River headwaters area, entered on Gowganda area[R]. Ontario Geological Survey Open File Report 5962, 1997.156.
[27]	Cheng Q, Agterbertg F P, Zhang S. Handling uncertainty in evidence construction and fuzzy weights of evidence predictive model[M]. UK: IAMG, 2003.
[28]	Cheng Q. Geodataanalysis system (GeoDAS)for mineral exploration: userʾs guide and exercise manual. Material for the training workshop on GeoDAS held at York University[EB/OL]. http://www.gisworld.org/geodas, 2000, Nov1-3.