Numerical Modeling of Seepage into Underground Openings in a Heterogeneous Continuum: A Sensitivity Study of Media Parameters
-
摘要: 影响任何一个地下废物处置场所长期行为的一个重要因素是进入地下废物贮置洞室内的渗流量的大小.预测地下洞室中的渗流量是困难的, 特别是当地下废物贮置洞室位于非均质非饱和带中.三维数值模型用于研究地下非均质中非饱和流动及流入地下洞室中的渗流量.讨论了非均质模型与均质模型的比较以及数值剖分尺度对计算结果的影响.进入洞室中的渗漏率随着引入系统中入渗量的增加而增大.选用4个参数来衡量渗流场的非均质程度: (1) 介质的平均渗透率K0; (2) VanGenuchten参数α; (3) 渗透率空间分布相关尺度; (4) 渗透率空间分布变化的标准差σ.根据一个随机实现的渗透率分布, 通过改变平均渗透率来研究其对流入洞室中渗透量的影响.对一个固定的入渗率而言, 流入洞室中的渗漏率将随着VanGenuchten参数α的减小而减小.模拟结果表明流入洞室的渗漏率与介质的平均渗透率相关, 即随平均渗透率的增大, 流入洞室的渗漏率亦增大.流入洞室的渗漏率还高度依赖于非均质渗透率场的空间分布相关长度与标准差.一个大的相关长度或高的标准差均能导致流入洞室的渗漏率增大.Abstract: The amount of water seeping into the waste emplacement underground openings is an important issue for the long-term performance of any underground waste repository. Seepage controls the corrosion rates of waste packages, the waste mobilization rates and transport rates of contaminant leaving the underground openings. Predicting the seepage rate is difficult under any circumstances, and is particularly complicated for repository sites located in unsaturated, heterogeneous media. In this study, a 3-D numerical model is used to study unsaturated flow and seepage through a heterogeneous medium into the underground openings with strongly variable parameters and boundary conditions. The model has been compared with homogeneous model. The seepage rate into the underground openings increases with an increase in percolation flux introduced into the system. Four parameters, (1) fracture continuum permeability, (2) Van Genuchten parameter α, (3) spatial correlation length and (4) standard deviation σ, are chosen to measure permeability-field heterogeneity. Based on a stochastically realized permeability distribution, the authors scale the mean permeability to study its effect on seepage into underground openings. For a chosen percolation flux, the seepage rate into the underground openings was reduced as the Van Genuchten parameter α decreased. Simulation results show that the seepage into the underground openings is sensitive to the mean permeability, with seepage rate decreasing as the mean permeability increased. Simulation results indicate that the seepage is also very sensitive to the correlation length and standard deviation of the heterogeneous field. Either a high correlation value or a high standard deviation σ value increases seepage into the underground openings for a substantially heterogeneous continuum.
-
Key words:
- underground openings /
- heterogeneous medium /
- unsaturated zone /
- seepage rate /
- sensitivity study /
- waste disposal.
-
进入地下废物处置洞室中的渗流量大小是影响任何一个地下废物处置场所长期行为的一个重要因素.这是因为渗流量的大小不仅控制了废物包装容器的腐蚀率、废物的活化度, 还决定着污染物质离开处置洞室的运移速率.Philip等[1] 1989年系统地提出了在均匀入渗条件下均质地下非饱和带中地下水渗流进入地下洞室的一般理论, 并发展了计算圆柱洞室中渗流量的解析解.在位于洞室的正上方, 当水流聚集并达到饱和的条件下水流开始进入洞室中.洞室周围的负压条件使水流处于非饱和状态.当渗流足够大时, 洞室周围介质场中的负压将随着地下水在洞室顶部的聚集而逐步减小.当负压无法维持与重力的平衡时, 渗流进入洞室的过程将发生.
天然介质的非均匀性可以提高渗流进入地下开挖洞室的可能性, 这是因为非均匀性提升了非饱和流场中饱和度与毛细压力(负压) 的变化[2, 3, 4].Birkholzer等[5]指出地下洞室附近岩石的渗流场非均匀性是引起渗流进入洞室的主要原因之一.
本文对渗流进入地下洞室进行了评价.首先利用随机方法来描述介质的水力学特性并产生渗流场的多个随机实现.然后利用数值模拟方法计算非饱和带地下水在多种条件下围绕地下洞室的运动.
1. 非均质模型
软件TOUGH2[6]用于模拟地下水在非饱和带中的运动.在计算中采用等温条件下单相的稳定流动.水流的运动可用下列水均衡方程来表示
(1) 其中, 假设密度ρ和粘度μ是常数; p是压力势(参考压力pr与毛细压力之和); g是重力加速度; 非饱和流动中的有效渗透率是饱和渗透率K和相对渗透率Kr的乘积.这里K是介质的特征系数, 它与流体及饱和度无关.而Kr是非饱和条件的函数, 其变化介于0~1之间, 即剩余饱和度与饱和度之间.非饱和流动中相对渗透率可以用一个非线性的相对渗透率/毛细压力模型来表示[7]
(2) 
(3) 
(4) 有效饱和度Se可写成
(5) 其中, S是饱和度, Sr是剩余饱和度, 1/α是进气压力, n是空隙大小分布特征参数或模型范围内裂隙宽度的空间变化率.
式(1) 表明非均匀介质中流动的变化受渗透率空间变化的制约, 同时受到式(2) 与式(3) 中特征函数参数α与n的空间变化的限制.在介质中, 我们模拟一个随机裂隙连续模型中的渗流问题.该裂隙连续模型考虑到了裂隙介质中流动的非均匀性.连续渗透率的某一变化可能起因于: (1) 裂隙隙宽的变化; (2) 裂隙密度的变化.在第1种条件下, 参数α从理论上讲与裂隙连续介质渗透率的平方根相关.在第2种条件下并无相关性.随机分析的结果表明, 与均匀参数α的条件相比, 考虑参数α与渗透率相关的条件下降低了渗流场的可变化性[2].Li和Tsang[8]指出与不考虑α参数与渗透率相关的模拟结果相比(即均匀参数α), 在考虑参数α与渗透率相关的模型中得到的渗流入洞室量偏小.本文选用固定的特征参数α和n, 假设隙宽的空间变化具有随机的均匀性.假定模型中特征参数n考虑了单裂隙中的隙宽变化及不同裂隙所形成裂隙连续介质的隙宽变化[5].
利用自美国内华达州Yucca山现场洞室尺度试验获得的67个空间渗透率值作为条件, 随机形成渗透率场[5].其中裂隙连续介质的渗透率的平均值为10-13 m2, 该分布自然对数值的标准差为2.1.
根据现场洞室的尺度及所处地层, 模型的范围选择为15 m宽(y方向), 20 m高(z方向) 及5.23 m长(x方向, 沿洞室方向).地下开挖洞室是一水平展布的圆柱状, 直径5.5 m.该洞室位于模拟区域的中下方.四周为零通量边界, 下部是重力排水边界, 上部是入渗流量边界(图 1).该流量根据区域模型中的相应地层中流量大小而定.该模型中假设开挖洞室是密封的, 其相对湿度接近100%, 即洞壁边界的毛细压力为零.为了检验该数值模型, Li和Tsang[9]将该数值模型与Philip等[1]的理论模型解析解进行了比较, 得到了很好的吻合.
1.1 非均质模型与均质模型对比
表 1列出了在本文基础方案中所使用的连续介质模型参数, 该组参数是在仔细分析已有现场数据的基础上确定的.现场数据是指美国内华达州Yucca山场址相应于永久核废物处置地层Tptpmn中的洞室裂隙分布图、钻孔摄影及渗透率现场试验数据[10, 11, 12, 13, 14].
表 1 基础方案中的参数组Table Supplementary Table Basecase parameters set used for fracture continuum in drift scale modeling
基础方案用于比较非均质模型与均质模型的计算结果.图 2分别给出了在上边界500 mm/a入渗条件下, 水饱和度在水平剖面及垂直剖面上的等值线图.在图中的上水平剖面上, 水流集中在高渗透率分布带.水流在低渗透率地带的缓慢流动导致了局部相对高饱和度的形成.在刚好位于洞室上方的水平剖面上, 由于开挖洞室的影响(零毛细压力边界), 洞室附近垂向流动缓慢, 水流在洞室附近汇集.在洞顶附近的某些部位, 当局部低渗透率阻碍了水流的向下运动时, 水流的汇集将更加明显.在这些特定的地区, 饱水度可能接近100%, 从而局部毛细压力趋近于零, 这时地下水渗流进入开挖洞室.
图 2 三维非均质渗流场中水平剖面(a) 和垂向剖面(b) 上水饱和度分布(入渗量为500 mm/a, 参数见表 1)Fig. 2. Saturation profiles on horizontal planes (a) and vertical planes (b) in a 3-D heterogeneous field for basecase properties and a percolation flux of 500 mm/year为了比较非均质模型与均质模型的差异, 在非均质的参数基础上建立均质模型, 使均质模型中的固定渗透率等于非均质模型中的统计平均渗透率.在相同的上部边界入渗量条件下, 在非均质模型中发现洞室中有渗漏水, 而均质模型中则没有(当入渗量小于70 mm/a时).相对于非均质模型, 均质模型则需要较高的入渗量条件才会发生地下水渗流入开挖洞室.图 3a给出了2种模型中渗漏率随着入渗量变化的曲线图.其中渗漏率定义为渗流进入洞室的水量与洞室在上部边界上投影面积内入渗量的比率.对比两种模型发现, 当上部入渗量达到一定大小时均匀模型可获得地下水渗流入洞室, 而当非均匀模型中地下水开始流入洞室时上部入渗量非常小, 仅是均匀模型的1/10左右.这说明在连续非均匀介质场中, 非均质及水流的选择性导致了洞室在较低的入渗量条件下发生地下水渗漏.这一现象也被Nitao[15]的研究工作所证实.他在模型研究中发现, 均质模型低估了洞室中的渗漏量, 这是因为均质模型无法刻画那些选择性的快速水流途径, 这些快速水流途径在较低的入渗量条件下导致了洞室中渗水.
图 3 渗漏率与入渗量、网格大小的关系曲线a.渗漏率与入渗量关系曲线; b. 3种剖分方案条件下3种随机实现的非均质模型中渗漏率与入渗量关系曲线; c.在50 mm/a和500 mm/a 2种入渗量(Qp) 条件下, 3种随机实现的非均质模型中渗漏率与网格大小的关系曲线Fig. 3. Seepage percentage as a function of percolation flux and grid size1.2 数值模型剖分
本节对3种剖分尺寸大小的非均质模型在一系列入渗量条件下进行了计算分析与比较.3种剖分网格的大小是0.5, 0.25及0.125 m.为了保证3种模型的可比较性, 3种剖分的模型范围不变, 介质的参数相同, 渗透率的空间分布相同.一系列入渗量分别为73.2, 150, 213.4, 275, 350, 425, 500 mm/a.
图 3b给出了3种剖分尺寸的非均质模型所计算得出的渗漏率与入渗量关系曲线图.每一剖分模型对应3个随机实现的非均质渗透率场.图 3c表明: 剖分网格越小, 渗流入洞室的量越大.然而与非均匀渗流场的影响(不同随机实现的非均质模型具有不同的渗漏率) 相比, 由于精细剖分所产生的渗漏率变化并不大.因此下面统一选用0.5 m的网格剖分模型来进行参数的灵敏度分析与讨论.
2. 非均匀介质参数的灵敏度分析
渗流进入地下洞室流量的相对大小(渗漏率) 与上部边界的入渗量的大小有关.图 4a给出了渗漏率与入渗量的关系曲线.在不同入渗量条件下, 对3个渗透率随机实现的分布进行了数值模拟.在每一数值模拟中计算水流的分布, 直至达到很高的时间水平, 以致于水流分布处于稳定状态.总的来看, 渗漏率随着入渗量的增加而增大.3种随机实现的渗漏率场模型均具有相同的趋势.然而由于许多非线性过程的介入, 渗漏率与入渗量的关系具有非线性.
图 4 基础方案条件下3种随机实现的非均质模型中渗漏率与入渗量(a)、介质平均渗透率(b) 的关系曲线; c.渗漏率和Van Genuchten参数1/α的关系曲线(b, c的入渗量为213 mm/a, 参数见表 1)Fig. 4. Seepage percentage as a function of percolation flux (a), mean permeability (b) for three realizations in the heterogeneous model with the basecase properties, and seepage percentage as a function of Van Genuchten parameter 1/α from 200 to 800 Pa with a percolation flux of 213 mm/year (c)渗漏率还受到非均匀介质参数的影响.衡量渗流场非均质程度的参数包括介质的几何平均渗透率参数、Van Genuchten参数α、渗透率空间分布变化的相关长度及标准差.下面分别就渗漏率对这4个参数的灵敏度进行分析与讨论.
2.1 渗透率
本文选用4个介质平均渗透率参数10-14, 10-13, 10-12及10-11 m2, 对3种随机实现的渗透率场模型进行计算模拟, 求出相应的水流渗入洞室中的相对大小——渗漏率.图 4b给出了这些模拟结果, 其他的模拟条件是入渗量213 mm/a, Van Genuchten参数1/α为1 000, 渗透率空间分布变化的相关长度是0.5 m, 标准差是1.66 (自然对数).
从图 4b中看出, 在给定参数及入渗量的条件下, 渗漏率将随着介质平均渗透率的减小而增大.当介质平均渗透率为10-11 m2时, 3种随机实现的渗透率模型均未发现地下水渗流进入洞室.由于洞室附近非饱和渗流的特性(即开挖洞室的零毛细压力障碍), 水流进入洞室很可能在低渗透率场的条件下发生.从平均意义上来讲, 在一定入渗量条件下, 平均渗透率越低, 水流移动越缓慢, 介质的含水量越高, 在地下洞室壁面上则可以发现更多的湿块(即饱和度近于1的局部).Philip等[1]的解析模型也揭示出渗漏率随着渗透率减小而增大的趋势.
2.2 Van Genuchten参数
渗漏率与Van Genuchten参数α、n有关.Li和Tsang[8]利用三维连续非均匀介质模型对Van Genuchten参数n进行了灵敏度分析.当提高参数n的值后, 数值模拟的结果表明渗漏率的变化很小.
选用4个Van Genuchten参数α, 相应1/α的值分别为200, 400, 600, 800 Pa, 来研究模拟流入洞室的渗漏量.图 4c给出了渗漏率与Van Genuchten参数1/α的相关曲线, 其中的模拟条件是入渗量213 mm/a、非均匀介质的平均渗透率为10-13 m2.该图表明渗漏率依Van Genuchten参数α的变化而改变, 当Van Genuchten参数α增大时(即1/α减小), 连续介质对水流的吸力减小, 从而导致更多的水渗漏进入地下洞室.
2.3 标准差
在基础方案中, 笔者选用的非均匀渗透率场的空间分布变化的标准差为σ=1.66 (取渗透率的自然对数).为了模拟分析渗透率场非均匀程度的标准差, 选用下列的简单公式来改变不同的标准差值
(6) 其中, k是基础方案中渗透率的自然对数值, k′是新的改变后的渗透率的自然对数值, k是平均渗透率的自然对数值, f是修改因子.式(6) 中, 可以通过选择不同的修改因子来改变非均匀的渗透率分布场:
f=0‚k′=k‚为均匀介质场;
f=1, k′=k, 为非均匀渗透率分布的基础方案;
f > 1, 为高度非均匀的渗透率分布场(相对于基础方案);
f < 1, 为低度非均匀的渗透率分布场(相对于基础方案).
设σ为基础方案中渗透率的自然对数的标准差, σ′为修改后渗流场中渗透率的自然对数的标准差, 可得出如下所示的两者关系式
(7) 根据式(7), 可以建立5个具有不同标准差的非均匀渗透率场模型, σ=0.5, 1.0, 1.66, 1.93, 2.5, 并用于灵敏度分析.
图 5a给出了基础方案中(σ=1.66) 在水流分布达到稳定时水饱和度的分布图.图 5b则列出了修改方案σ=1.0 (即相对低度非均匀的渗透率分布场) 中水流分布稳定时, 水饱和度的分布D图.从2个图中均可看出水流自上而下沿着选择性的通道运动, 即由高渗透率单元所连接的通道.可发现在图 5a中有较多的水流汇集在洞室的附近并绕着洞壁向下运动.
图 5 2种渗透率的自然对数标准差条件下水饱和度分布(入渗量为213 mm/a, 参数见表 1)Fig. 5. Saturation profiles for the standard deviation σ of ln k=1.66 (a) and 1.0 (b) with basecase properties and a percolation flux of 213 mm/year图 6a给出了渗漏率与非均匀渗透率的标准差的关系曲线.在固定其他参数的条件下, 对应于高标准差的模型(即高度非均质渗流场) 笔者获得了大的进入洞室的渗漏率.这是因为, 对于低的标准差模型, 流场变化起伏不大并趋向于均匀介质方案, 水流较容易地流经大部分围绕洞室的流场, 从而流出下部边界.而另一方面, 对于具有高标准差的高度非均匀渗流介质场而言, 则有更多的水流沿着选择性的通道运动, 并容易汇集在洞室的上方, 从而有更多的机会流入洞室.
图 6 a.3种随机实现的非均质模型中渗漏率与渗透率空间变化的自然对数标准差(σ) 关系曲线; b.5种随机实现随机模拟结果的平均渗漏率与渗透率空间分布的相关长度(λ) 关系曲线Fig. 6. Seepage percentage as a function of the standard deviation σ (in natural log) of permeability for three realizations of the heterogeneous model for a percolation flux of 73.2 mm/year (a); Mean seepage percentage over five realizations as a function of correlation length for the basecase with a percolation flux of 213 mm/year (b)2.4 空间分布相关长度
本节选用3个非均匀介质渗透率空间分布的相关长度值0.5, 1.0, 4.0 m, 对5种随机实现的渗透率场模型进行计算模拟.图 6b给出了由5种随机实现模型所计算出的平均渗漏率与渗透率空间分布的相关长度关系曲线图.其他的参数条件是: 入渗量是213 mm/a, 介质的平均渗透率是10-13 m2, 标准差为1.66.曲线显示出总的趋势是渗透率空间分布的相关长度越大, 模型所获得的洞室渗漏率越高.
图 7给出了渗透率空间分布长度分别为1 m和4 m的2种模型渗透率场分布图.图 8则给出了相对于图 7中2种模型模拟结果中水饱和度的空间分布图.对比两图不难看出, 地下水在地下非饱和带中开挖洞室附近的流动明显地受到介质非均匀分布的影响.
图 7 2种渗透率空间分布相关长度1 m (a) 与4 m (b) 条件下的非均匀渗透率空间分布Fig. 7. Heterogeneous permeability fields for the correlation length 1 m (a) and 4 m (b)
图 8 2种渗透率空间分布相关长度1 m (a) 与4 m (b) 条件下水饱和度的空间分布(入渗量为213 mm/a)Fig. 8. Saturation profiles for the correlation length of 1 m (a) and 4 m (b) with basecase properties and a percolation flux of 213 mm/year3. 结语与讨论
本文利用数值模型模拟水流渗漏进入地下开挖洞室现象.在分析现有场地实测渗透率等参数的基础上, 利用随机方法建立了渗透率非均匀空间分布的渗流场.选用多个随机实现来揭示和表现渗透率场空间变化的不确定性.通过均匀介质模型与非均匀介质模型的分析与比较, 论述了水流在非饱和带中围绕开挖洞室的非均匀渗透率场中的分布特征.
文中对刻画渗流场非均匀分布程度的参数进行了灵敏度分析.这4个参数是: 连续介质的渗透率、Van Genuchten参数、渗透率空间分布的相关长度及渗透率的自然对数的标准差.模拟结果表明, 进入地下洞室的渗漏率与这4个参数密切相关.渗透率将随着入渗量的增加而增大.在固定的入渗条件下, 渗漏率随着介质平均渗透率的增加而减小, 随着Van Genuchten参数α的增加而减小.对于具有高标准差的非均匀渗透率空间分布场, 即高度非均质渗流场, 模拟结果得出了较高的渗漏率进入洞室中.从平均值上看, 一个具有较高相关长度值的非均匀渗透率空间分布场模型计算出较高的洞室渗漏率.然而对于多种随机实现的连续非均匀介质模型计算结果而言, 由较高相关长度值得出的渗漏率变化范围较大.
非均匀介质参数灵敏度分析的结果说明了地下洞室的渗漏率受参数变化的影响程度, 该成果可用于确定选择不同参数的范围大小, 从而指导设计地下开挖洞室(如用于废物处置场所或地下隧道等) 长期行为的风险评价方案.
致谢: 感谢韩巍先生对初稿的打印与整理 -
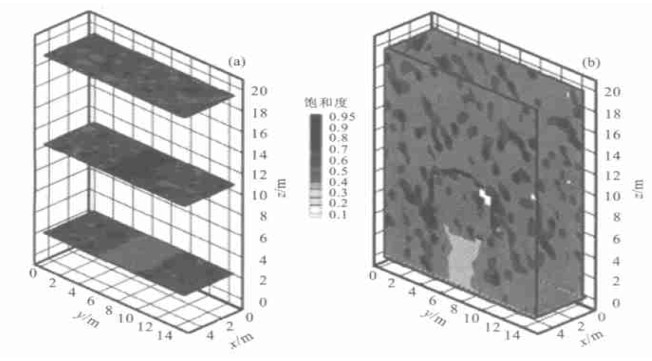
图 2 三维非均质渗流场中水平剖面(a) 和垂向剖面(b) 上水饱和度分布(入渗量为500 mm/a, 参数见表 1)
Fig. 2. Saturation profiles on horizontal planes (a) and vertical planes (b) in a 3-D heterogeneous field for basecase properties and a percolation flux of 500 mm/year
图 3 渗漏率与入渗量、网格大小的关系曲线
a.渗漏率与入渗量关系曲线; b. 3种剖分方案条件下3种随机实现的非均质模型中渗漏率与入渗量关系曲线; c.在50 mm/a和500 mm/a 2种入渗量(Qp) 条件下, 3种随机实现的非均质模型中渗漏率与网格大小的关系曲线
Fig. 3. Seepage percentage as a function of percolation flux and grid size
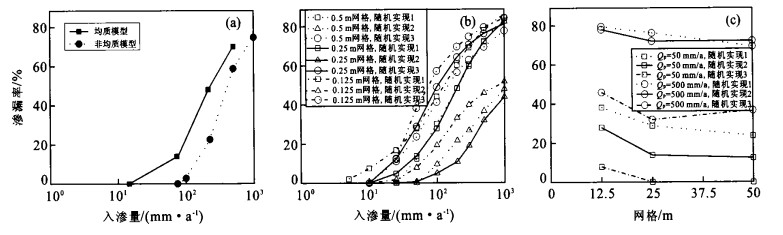
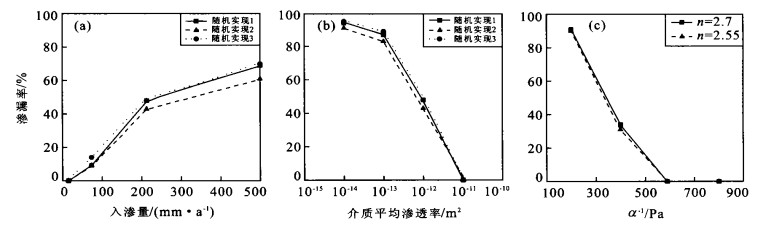
图 4 基础方案条件下3种随机实现的非均质模型中渗漏率与入渗量(a)、介质平均渗透率(b) 的关系曲线; c.渗漏率和Van Genuchten参数1/α的关系曲线(b, c的入渗量为213 mm/a, 参数见表 1)
Fig. 4. Seepage percentage as a function of percolation flux (a), mean permeability (b) for three realizations in the heterogeneous model with the basecase properties, and seepage percentage as a function of Van Genuchten parameter 1/α from 200 to 800 Pa with a percolation flux of 213 mm/year (c)
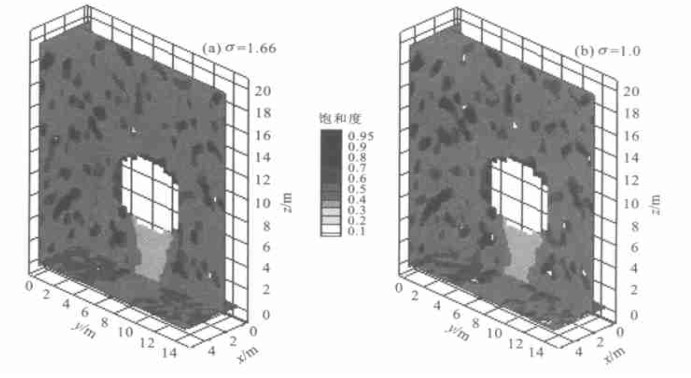
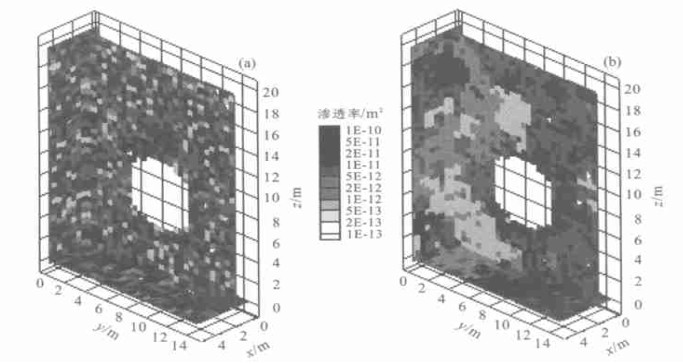
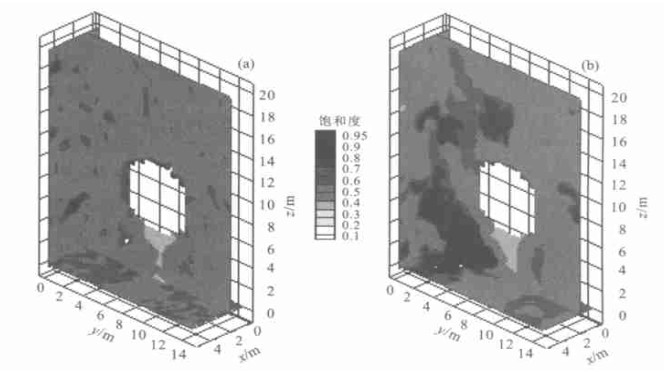
图 5 2种渗透率的自然对数标准差条件下水饱和度分布(入渗量为213 mm/a, 参数见表 1)
Fig. 5. Saturation profiles for the standard deviation σ of ln k=1.66 (a) and 1.0 (b) with basecase properties and a percolation flux of 213 mm/year
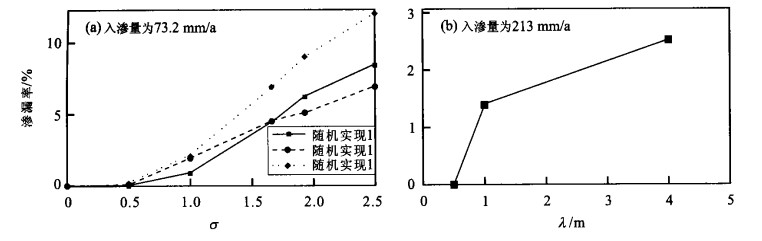
图 6 a.3种随机实现的非均质模型中渗漏率与渗透率空间变化的自然对数标准差(σ) 关系曲线; b.5种随机实现随机模拟结果的平均渗漏率与渗透率空间分布的相关长度(λ) 关系曲线
Fig. 6. Seepage percentage as a function of the standard deviation σ (in natural log) of permeability for three realizations of the heterogeneous model for a percolation flux of 73.2 mm/year (a); Mean seepage percentage over five realizations as a function of correlation length for the basecase with a percolation flux of 213 mm/year (b)
图 7 2种渗透率空间分布相关长度1 m (a) 与4 m (b) 条件下的非均匀渗透率空间分布
Fig. 7. Heterogeneous permeability fields for the correlation length 1 m (a) and 4 m (b)
图 8 2种渗透率空间分布相关长度1 m (a) 与4 m (b) 条件下水饱和度的空间分布(入渗量为213 mm/a)
Fig. 8. Saturation profiles for the correlation length of 1 m (a) and 4 m (b) with basecase properties and a percolation flux of 213 mm/year
表 1 基础方案中的参数组
Table 1. Basecase parameters set used for fracture continuum in drift scale modeling
-
[1] Philip J R, Knight J H, Waechter R T. Unsaturated seepage and subterranean holes: Conspectus and exclusion problem for circular cylindrical cavities[J]. Water Resour Res, 1989, 25: 16-28. doi: 10.1029/WR025i001p00016 [2] Yeh T-C J, Gelhar L W, Gutjahr A L. Stochastic analysis of unsaturated flow in heterogeneous soils: 1. Stochastically isotropic media[J]. Water Resour Res, 1985, 21: 447-456. doi: 10.1029/WR021i004p00447 [3] Yeh T-C J, Gelhar L W, Gutjahr A L. Stochastic analysis of unsaturated flow in heterogeneous soils: 2. Stochastically isotropic media with variable α[J]. Water Resour Res, 1985, 21: 457-464. doi: 10.1029/WR021i004p00457 [4] Yeh T-C J, Gelhar L W, Gutjahr A L. Stochastic analysis of unsaturated flow in heterogeneous soils: 3. Obervation and applications[J]. Water Resour Res, 1985, 21: 465-471. doi: 10.1029/WR021i004p00465 [5] Birkholzer J T, Li G, Tsang C-F, et al. Modeling studies and analysis of seepage into drifts at Yucca Mountain [J]. J Contaminant Hydrol, 1999, 38 (1 -3): 349 - 384. [6] Pruess K. TOUGH2-A general purpose numerical simulator for multiphase fluid and heat flow[R]. Report LBL-29400, Lawrence Berkeley National Laboratory, Berkeley, California, 1991. [7] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soil[J]. Soil Sci Soc J, 1980, 44: 892-898. doi: 10.2136/sssaj1980.03615995004400050002x [8] Li G, Tsang C-F. Seepage model for PA including drift collapse, MDL-NBS-HS-000002 REV01[DB/OL]. CRWMS M&O, Las Vegas, Nevada, 2000. [9] Li G, Tsang C-F. Seepage into drift with mechanical degradation[J]. J Contaminant Hydrol, 2003, 62-63: 157-172. doi: 10.1016/S0169-7722(02)00171-7 [10] Sonnenthal E, Ahlers C F, Bodvarsson G S. Fracture and fault properties for the UZ site-scale flow model [R]. Yucca Mountain Project Milestone Report SP24UFM4, Lawrence Berkeley National Laboratory Report LBNL-40376, Berkeley, CA, 1997. [11] Tsang Y W, Cook P. Ambient characterization of the ESF drift scale test area by field air-permeability measurements[R]. Yucca Mountain Project Milestone Report SP9512 M4, Lawrence Berkeley National Laboratory, Berkeley, CA, 1997. [12] Wang J S Y, Trautz R C, Cook P J, et al. Field tests and model analyses of seepageinto drift[J]. J Contaminant Hydrol, 1999, 38 (1-3): 323-347. doi: 10.1016/S0169-7722(99)00019-4 [13] Tsang Y W, Birkholzer J T. Multiphase thermal-hydrological processesin thesingle heater test at Yucca Mountain[J]. J Contaminant Hydrol, 1999, 38(1-3): 385 -425. doi: 10.1016/S0169-7722(99)00021-2 [14] FinsterleS, Ahlers C F, Trautz R C. Seepage calibration model and seepage testing data, MDL-NBS-HS000004 REV01[DB/OL]. Civilian Radioactive Waste Management System Management and Operating Contractor (CRWMS M&O): Las Vegas, Nevada. Lawrence Berkeley National Laboratory, Berkeley, CA, 2000. [15] Nitao J S. Preliminary bounds for the drift-scale distribution of percolation and seepage at the repository level under pre-emplacement conditions[R]. Yucca Mountain Project Deliverable No. SPLB1 M4. Lawrence Livermore National Laboratory, Livermore, California, 1997. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 3621
- HTML全文浏览量: 560
- PDF下载量: 19
- 被引次数: 0
