Analysis of Heterogeneous Soil Water Using Information Entropy and Multifractal Theory
-
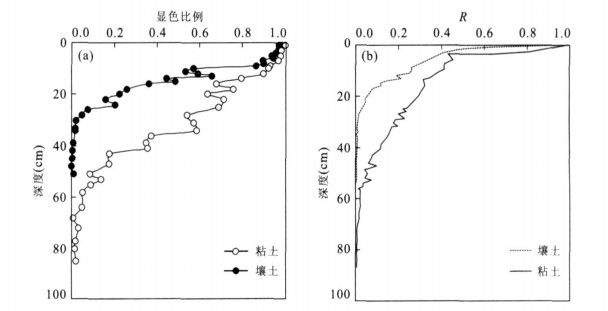
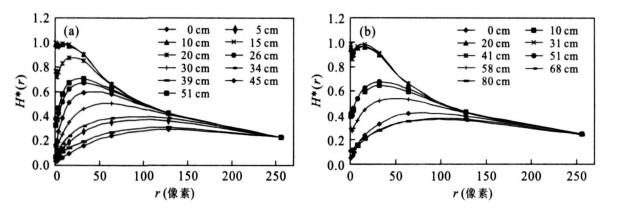
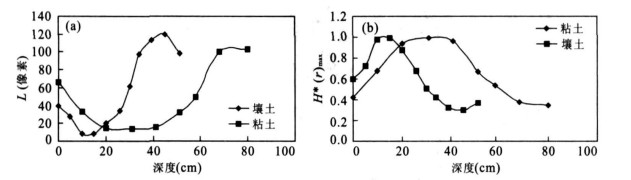
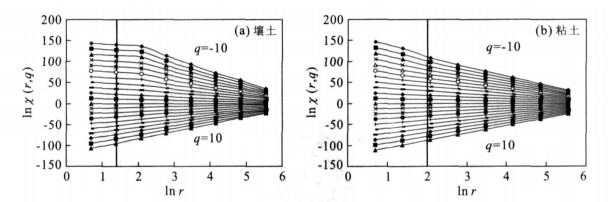
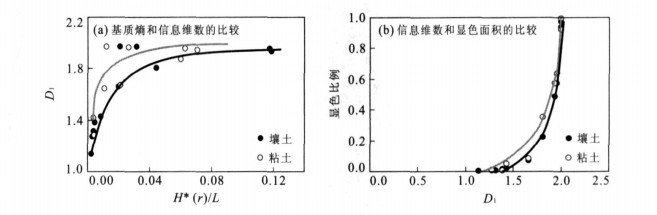
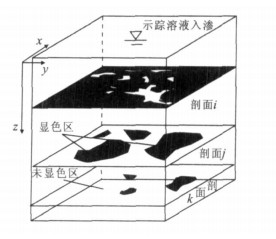
摘要: 根据粘土和壤土中非均匀水流运动的示踪试验, 研究了土壤水非均匀流动模式, 并基于信息熵与多重分形理论探讨了多孔介质中流动的非均匀性质.不同土质试验研究的分析结果表明, 各深度信息熵与特征长度具有相反的变化趋势.非均匀流动多重分形特性分析表明, 非均匀流动分布具有很强的自相似性, 但并不是在所有研究尺度范围内都满足标度不变性, 在显色比例相近的情况下, 壤土和粘土中水流运动标度不变性的范围表现出显著的差异.Abstract: The major objective of this study is to investigate the heterogeneity of soil water flow. Field experiments were performed in loam and clay soil and an iodine-starch staining method was applied to visualize flow paths in the soil. Heterogeneous flow patterns were described by using information entropy and multifractal theory.Resultsshow that information entropy increases with decreasingly characteristic length, which is a scale used to characterize flow stained patterns. The soil flow heterogeneity is similar at different measurement scales. However, the variance of flow distributions change with scales. In the loam soil, scaling invariance of water flow distributions is in a larger range than that in the clay soil.
-
多孔介质中流动表现出复杂的动力状态, 土壤介质信息的空间变异性和流动非线性(不稳定性) 使得连续性模型的实际应用受到了很大的限制, 主要表现在流体运动的各向异性、尺度效应和流动非线性(Kravchenko et al., 1999; Liu et al., 2003).高度变异性和各向异性是土壤的基本特性, 流动的非线性又使得土壤中水和溶质的运动更加不确定.近年来的试验观测结果表明, 土壤中水流运动具有分形(多重分形) 性质(Olsson et al., 2002; Tarquis et al., 2006; Wang et al., 2006; 王康等, 2007).分形(多重分形) 是影响流动的各种因素综合作用的结果, 包含了流动性质、介质结构等多方面的信息.研究流动分形(多重分形描述) 所包含的信息量和信息特性有助于深入了解非均匀流动特性.
非均匀流动具有尺度特性(Olsson et al., 2002; Tarquis et al., 2006; Wang et al., 2006; 王康等, 2007).分形(多重分形) 描述不同尺度之间的自仿射关系, 然而现有的研究更多地探讨自仿射关系, 对于自仿射关系与测量尺度之间变化关系的研究则鲜有报道.此外, 从理论上讲, 分形是无限的, 然而在实际情况下, 采用有限分形迭代刻画实际流动问题将更为合理, 非均匀流动分形(多重分形) 下上限也需要进一步的研究.本文通过试验研究, 探讨以下问题: (1) 非均匀水流运动特性与流动信息特性; (2) 不同测定尺度条件下, 水流运动多重分形自仿射关系的变化; (3) 描述非均匀水流运动多重分形度的极限关系.
1. 非均匀流动试验研究
试验于2007年4月在武汉大学灌溉排水与水环境综合试验场进行.试验布置如图 1所示, 试验在原状土条件下进行, 试验区域为100×100 cm2, 土体深100 cm.试验开始时, 在土体表面灌入水头高度为60 mm的碘化钾示踪剂溶液, 当示踪剂溶液完全渗入地表之后, 将试验区用防水和隔热材料覆盖; 24 h后在水平方向开挖剖面, 并向剖面喷洒淀粉溶液, 入渗水流经过的区域, 由于含有的碘与淀粉反应, 显现蓝色, 水流没有经过的区域, 则土壤颜色不发生变化, 由此可确定流动区域和非流动区域.由于碘在分子状态才能够与淀粉反应, 因此采用Fe (NO3) 3将碘离子完全氧化为碘分子并加速反应时间, 喷洒淀粉10 min后颜色充分显现, 用CCD相机照相记录显色模式.试验在白天进行, 照相时避免阳光直接照射以及对阳光进行散射.试验在非饱和状态下进行, 试验前测定了初始土壤含水率.两组试验分别在粘土和壤土条件下进行, 土壤物理性质和水动力参数如表 1所示.
表 1 试验土壤物理和水动力性质Table Supplementary Table Physical and hydraulic properties of the experimental soils
两组试验条件下, 土壤水流均表现出明显的非均匀运动特性, 图 2a、2b所示.图 3a为两组试验显色面积比例比较, 可以看出, 仅在0~5 cm深度, 区域完全显色, 出现非显色区域后(发生局部流动), 显色面积将随深度迅速下降.
图 2 不同土壤深度显色模式a.粘土深度为5cm、10cm、20cm、40cm和80cm显色模式; b.壤土深度为5cm、10cm、20cm、30cm和50cm深度显色模式Fig. 2. Heterogeneous stained patterns at various depths
图 3 显色比例、流动模式相关程度R的比较Fig. 3. Comparison of dye coverage, correlativity of water flow pattern in stained regions after infiltration采用(1) 式分析非均匀流动模式相关程度与剖面距离之间的关系(Yasuda et al., 2001) :
(1) 式(1) 中, 如果水平剖面(x, y) 位置(水平层取样深度为z) 入渗水流经过, 被显色, 则f (x, y, z) =1;反之, f (x, y, z) =0;rz为相关距离, D为流动区域.两组试验的相关程度如图 3b所示.可以看出, 水平剖面之间的流动相关程度随剖面距离的增加而表现出指数递减的趋势, 粘土情况下显色区域变化相对较为平缓, 相同距离的流动相关程度也较大.比较图 3a、3b可以看出, 剖面流动模式相关程度与显色比例的变化程度具有一致性.
2. 非均匀流动多重分形信息特性和尺度相关性分析
2.1 非均匀流动信息特性分析
信息熵是描述信息特性的一种方法(Shannon, 1948; Andraud et al., 1994), 可以有效地度量随机变量的不确定性和信息量.系统的信息熵被定义为系统状态的平均值:
(2) 采用不同直径的箱盒对非均匀流动信息特性进行考察, 用测量尺度为r的箱盒覆盖尺寸为R的流动区域, 则箱盒内包含j个显色像素的箱盒概率为:
(3) 式(3) 中, Nj (r) 为含有j个显色像素点的盒子数, n (r) 是在尺度r下的盒子总数.根据显色像素数目分布考察非均匀流动信息量:
(4) 对H (r) 进行标准化可得:
(5) 式(5) 中, Hmax (r) =ln (r2+1), 对应最大信息熵值H* (r) max的盒子尺度被称为特征长度L.
图 4a、4b分别为壤土和粘土不同深度土壤剖面信息熵随着测定尺度r的变化, 可以看出, 壤土和粘土两种情况下各深度信息熵表现出相同的变化趋势: 先增加至峰值, 随后减小.图 5为壤土和粘土的特征长度值L与信息熵最大值H* (r) max随深度变化的变化情况, 随土壤深度增加, 信息熵最大值H* (r) max先增加后减小, 特征长度则随土壤深度增加显示出先减小、后增加的变化趋势, 且信息熵最大值达到峰值时, 特征长度亦减小到最小值.比较图 3a和图 5b可知, 粘土深度为31 cm的土壤剖面显色比例为57.28%, 其信息熵达到整个剖面系列的最大值, 而壤土在深度为15 cm的土壤剖面显色比例为48.74%, 其信息熵达到整个剖面系列的最大值, 在显色比例接近50%的深度位置, 其标准信息熵值出现最大值, 且接近于1, 粘土和壤土情况下, 标准信息熵都表现出相同的变化规律.比较图 3和图 5亦可以看出, 显色面积随深度的递减程度明显地大于信息熵的递减程度.这表明流动过程中, 非均匀流动不确定性和复杂性是逐渐增加的, 但由于显色面积的快速下降导致了整体非均匀信息量的减少.
图 4 不同土壤深度下标准化信息熵随尺度变化分析Fig. 4. Normalized configuration entropy (H * (r)) versus box size (r) from horizontal sections at different depths
图 5 特征长度(a)与信息熵最大值(b)随土壤深度变化Fig. 5. The change of characteristic length (a) and information entropy (b) at different depths2.2 非均匀流动多重分形特性分析
以特征尺度r的箱盒覆盖试验区域, 每一个箱盒中对于质量度μi (r) (显色像素的数目) 用Holder指数(Feder, 1988) 进行描述:
(6) 由(6) 式可知, α值越大, 则质量度越小, 反之亦然.多重分形分析理念在于将测定尺度为r、具有相同质量度α的箱盒进行群组, 进而通过分析箱盒项目随测定尺度减少而增加的速率, 对流动非均匀性质从不同尺度进行描述.
根据多重分形关系, 以不同的测量阶矩q考察系统的质量度, 则:
(7) 式(7) 中, n (r) 为测定尺度为r情况下的箱盒总数, τ (q) 为质量指数.ln χ (r, q) -lnr关系曲线斜率:
(8) 式(8) 中, χ (r, q) 为q阶配分函数.
(9) lnχ (r, q) -lnr曲线的线性范围称为标度不变范围, 只有满足标度不变性并在标度不变范围内才能求得准确的多重分形谱.广义分形维数Dq定义为:
(10) 为了对不同土质下非均匀流动多重分形特性进行分析更具有可比性, 选取显色比例相近剖面的流动分形性质进行比较, 粘土选用土壤深度为9 cm (显色比例0.931), 相似显色比例情况下壤土选择深度为5 cm (显色比例0.939).
图 6a、6b分别为壤土(土壤深度5 cm) 和粘土(土壤深度9 cm) 情况下lnχ (r, q) -lnr关系曲线, 两种土壤lnχ (r, q) -lnr表现出相似的规律.其双对数图具有很好的拟合度, 表明非均匀流动分布具有很好的自相似性和分形特征.在q≥1时, lnχ (r, q) -lnr基本上保持为直线, 而q < -1时, 曲线分为两段, r大的区域斜率绝对值大, r小的区域斜率绝对值较小.也就是说, 不是在所有r范围内都满足标度不变性.这种异常现象的出现与小概率呈现异常的涨落有关.由于盒子计数中可能出现象素很小的染色图形碎片, 此时最小pij (r) 不随r的减小而继续减小, 于是对应的χ (r, q) 在q < -1时的值下降速度开始异常的缓慢.
图 6 壤土和粘土lnχ(r, q)- In(r)曲线Fig. 6. Bi-log plot of χ(r, q) versus box size (r) for the loam and clay soil信息熵((4) 式) 和信息维数((10) 式) 概念一致, 描述某一测定尺度情况下非均匀流动信息量.非均匀流动信息量越大, 则流动不确定性和复杂性也越为显著.考虑到最大信息熵与测定尺度有关, 两组试验基质熵(H* (r) /L) 和信息维数的比较如图 7a所示, 可以看出, 随着信息熵的增加, 信息维数整体表现出非线性增长的趋势.由于最大信息熵是某一特征尺度情况下的最大值, 而信息维数是最小测量尺度情况下得到的.因此, 两者之间的距离为最小测量测度下度量非均匀流动信息量与最大信息量之间的差异.显然这种差异和非均匀流动特性有关, 粘土和壤土最大信息熵和信息维数表现出不同的关系.图 7b为两组试验信息维数和显色面积的比较, 可以看出, 小于50%显色比例剖面, 信息维数随显色面积增加而逐渐增大, 而显色面积比例超过50%, 则信息维数变化幅度比较有限.
图 7 基质熵、信息维数与显色面积关系比较Fig. 7. (a) Potential entropy (H* (r)/ L) vs. information dimension; (b) fractal dimension vs. iodine stained coverage for different soils3. 结论
(1) 在粘土和壤土情况下开展了非均匀水流运动显色示踪试验, 对非均匀流动信息量和流动多重分形性质进行了分析.
(2) 不同特征尺度情况下的流动非均匀信息状态表明: 水流非均匀流动过程中, 反映流动信息量(不确定程度) 的信息熵最大值H* (r) max先增加后减小, 而特征长度则表现出相反的变化趋势.流动由均匀流过渡到非均匀流后, 非均匀信息量(不确定性和复杂性) 增加, 但是显色面积随深度的递减程度明显的大于信息熵的递减程度, 由于显色面积的快速下降导致了整体非均匀信息量的减少, 抵消了非均匀流动不确定性和复杂性的增加量.壤土和粘土情况下的试验结果显示出相同的变化规律.
(3) 非均匀流动多重分形特性分析表明, 非均匀流动分布具有很好的自相似性, 具有分形特征, 但是不是在所有r范围内都满足标度不变性.粘土和壤土中非均匀流动表现出相同的多重分形特性, 同时也表明标度不变性尺度与土壤质地有关.
-
图 2 不同土壤深度显色模式
a.粘土深度为5cm、10cm、20cm、40cm和80cm显色模式; b.壤土深度为5cm、10cm、20cm、30cm和50cm深度显色模式
Fig. 2. Heterogeneous stained patterns at various depths
图 3 显色比例、流动模式相关程度R的比较
Fig. 3. Comparison of dye coverage, correlativity of water flow pattern in stained regions after infiltration
图 4 不同土壤深度下标准化信息熵随尺度变化分析
Fig. 4. Normalized configuration entropy (H * (r)) versus box size (r) from horizontal sections at different depths
图 5 特征长度(a)与信息熵最大值(b)随土壤深度变化
Fig. 5. The change of characteristic length (a) and information entropy (b) at different depths
图 6 壤土和粘土lnχ(r, q)- In(r)曲线
Fig. 6. Bi-log plot of χ(r, q) versus box size (r) for the loam and clay soil
图 7 基质熵、信息维数与显色面积关系比较
Fig. 7. (a) Potential entropy (H* (r)/ L) vs. information dimension; (b) fractal dimension vs. iodine stained coverage for different soils
表 1 试验土壤物理和水动力性质
Table 1. Physical and hydraulic properties of the experimental soils
-
Andraud, C., Beghdadi, A., Lafait, J., 1994. Entropic analysis of random morphologies. Physica A: Statistical and Theoretical Physics, 207 (1-3): 208-212. doi: 10.1016/0378-4371(94)90374-3 Feder, J., 1988. Fractals. Plenum Press, New York. Kravchenko, A. N., Boast, C. W., Bullock, D. G., 1999. Multifractal analysis of soil spatial variability. Agron. J., 91: 1033-1041. doi: 10.2134/agronj1999.9161033x Liu, H. H., Zhang, G. X., Bodvarsson, G. S., 2003. The active fracture model: Its relation to fractal flow patterns and an evaluation using field observations. Vadose Zone Journal, 2: 259-269. Olsson, J., Persson, M., Albergel, J., et al., 2002. Multiscaling analysis and random cascade modeling of dye infiltration. Water Resources Research, 38: 1263. doi: 10.1029/2001WR00080. Shannon, C. E., 1948. A mathematical theory of communication. Bell Syst. Tech. J., 27: 379-423. doi: 10.1002/j.1538-7305.1948.tb01338.x Tarquis, A. M., McInnes, K. J., Keyb, J. R., et al., 2006. Multiscaling analysis in a structured clay soil using 2D images. Journal of Hydrology, 322 (1-4): 236-246. doi: 10.1016/j.jhydrol.2005.03.005 Wang, K., Zhang, R. D., Wang, F. Q., et al., 2007. Characterizing scale-dependent heterogeneity of soil water movement through dying infiltration experiments. Advances in Water Science, 18 (2): 158-163 (in Chinesewith English abstract). Wang, K., Zhang, R. D., Yasuda, H., 2006. Characterizing heterogeneity of soil water flow by dye infiltration experi ments. Journal of Hydrology, 328 (3-4): 559-571. doi: 10.1016/j.jhydrol.2006.01.001 Yasuda, H., Berndtsson, R., Persson, H., et al., 2001. Characterizing preferential transport during flood irrigation of a heavy clay soil using the dye Vitasyn Blau. Geoderma, 100 (1-2): 49-66. doi: 10.1016/S0016-7061(00)00080-X 王康, 张仁铎, 王富庆, 等, 2007. 土壤水分运动空间变异性尺度效应的染色示踪入渗试验研究. 水科学进展, 18 (2): 158-163. doi: 10.3321/j.issn:1001-6791.2007.02.002 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 4170
- HTML全文浏览量: 506
- PDF下载量: 75
- 被引次数: 0
