DYNAMIC MECHANISM AND FRACTAL SIMULATION OF GROWTH PROCESS OF FAN-SHAPED SEDIMENTARY BODIES
-
摘要: 扇形沉积体是我国内陆及近海中、新生代含油气盆地的重要油气聚集体, 如何定量地表征沉积体的分布状况及内部结构参数的空间变化规律, 对指导油气勘探具有重要意义.扇形沉积体的生长过程是一个复杂的非线性动力学过程, 通过对其生长的沉积动力学、混沌动力学和分形动力学机制的分析, 认识到扇形沉积体的生长具有分形特征, 决口过程是造成其外部形态复杂多变的重要原因; 分形几何学理论在沉积体定量建模和模拟方面具有较好的应用前景.采用分形-地质统计学相结合的方法, 对扇形沉积体的外部形态和内部结构特征实施了计算机模拟, 并对模拟结果进行了讨论.Abstract: Fanshaped sedimentary bodies are important oil-gas accumulation bodies for the Mesozoic and Cenozoic oil- and gas-bearing basins in the inland and offshore of China. The quantified characterization of the spatial distribution pattern of the sedimentary bodies and that of the spatial variation principle of the inner structure parameters, are of important significance to the oil and gas exploration. The growth process of a fan-shaped sedimentary body is a complex nonlinear dynamic process. The analysis of the sedimentary dynamic, chaotic dynamic and fractal dynamic mechanisms of the growth process concludes that the growth process of the fan-shaped sedimentary bodies has fractal features. The crevasse process is an important cause for the complex and changing surface shapes of the sedimentary bodies. The fractal geometry theory will be relatively well applied to the quantitative modeling and simulation of the sedimentary bodies. The combination of fractal with geostatistics is applied to simulation the surface shapes and internal structures of the fan-shaped sedimentary bodies. In addition, a discussion of the simulation results is presented.
-
Key words:
- fan-shaped sedimentary body /
- sedimentary dynamics /
- chaos /
- fractal /
- geostatistics /
- computer simulation
-
图 1 洱海弥苴河三角洲的分形生长模型
1~6为演化阶段, 数据为分形盒维数
Fig. 1. Fractal growth model of Miqie River delta, Erhai in Yunnan Province
图 2 河控鸟足状三角洲的决口(a)和高级分支现象(b)
Fig. 2. Crevasse (a)and advanced branch (b)of a fluvial-dominated bird-foot delta
图 4 冲积扇砂体平面形态模拟结果(过关键控制点)
Fig. 4. Modeling result of plane form of an alluvial fan sandbody
-
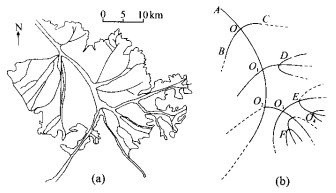
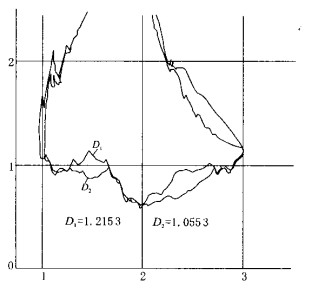
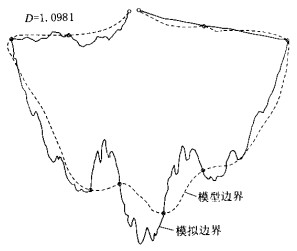
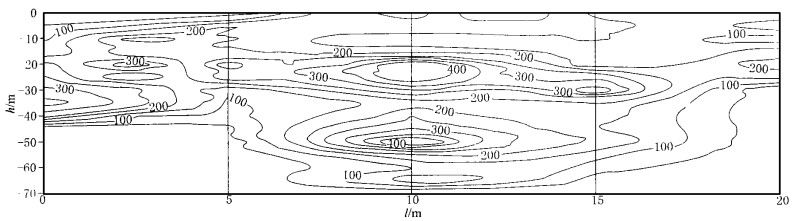
[1] 吴崇筠, 薜叔浩. 中国含油气盆地沉积学[M]. 北京: 石油工业出版社, 1992. [2] 丘东洲, 何治亮. 陆盆扇体沉积的形成机制及其油气意义[A]. 见: 中国石油学会石油地质委员会编. 碎屑岩沉积相研究[C]. 北京: 石油工业出版社, 1988. [3] 王寿庆. 扇三角洲模式[M]. 北京: 石油工业出版社, 1993. [4] 王域辉, 廖淑华. 分形与石油[M]. 北京: 石油工业出版社, 1994. [5] 张一伟, 刘洛夫, 欧阳建平, 等. 油气藏多学科综合研究: 分形几何学在储层非均质性描述中的应用[M]. 北京: 石油工业出版社, 1995.184~190. [6] 周江羽, 吴冲龙, 毛小平, 等. 含油气盆地储层建模和模拟研究评述[J]. 地质科技情报, 1998, 17(1): 67~72. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ801.014.htm [7] 周江羽, 袁艳斌, 李星. 地学分形研究中值得注意的几个问题[J]. 地质科技情报, 1999, 18(2): 93~96. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ902.027.htm [8] 金强, 曾怡, 任怀强, 等. 两口井条件下的储层参数预测方法[J]. 石油实验地质, 1995, 17(1): 26~33. https://www.cnki.com.cn/Article/CJFDTOTAL-SYSD501.003.htm [9] Barton C C, LaPointe P R. Fractals in petroleum geology and earth processes[M]. New York and London: Plenum Press, 1995. [10] Hewett T A, Behrens R A. Conditional modeling of reservoir heterogeneity with fractals[J]. SPE Formation Evaluation, 1990, 5(3): 217~225. doi: 10.2118/18326-PA [11] Eivind D, TiΦlwen C B. A two-stage stochastic model applied to a North Sea reservoir[J]. JPT, 1992, 44(4): 402~408. doi: 10.2118/20605-PA [12] 盖洛韦W E, 霍布德D K. 陆源碎屑沉积体系在石油、煤和铀勘探中的应用[M]. 北京: 石油工业出版社, 1989. [13] 李思田. 含能源盆地沉积体系[M]. 武汉: 中国地质大学出版社, 1996. [14] 克莱因G deVries. 砂岩沉积模式与能源矿产勘探[M]. 李思田, 李宝芳, 林畅松译. 北京: 地质出版社, 1989. [15] 冯增昭, 王英华, 刘焕杰, 等. 中国沉积学[M]. 北京: 石油工业出版社, 1994. [16] 焦养泉, 李思田, 李祯, 等. 曲流河与湖泊三角洲沉积体系及典型骨架砂体内部构成分析. 武汉: 中国地质大学出版社, 1995. [17] 周江羽. 断陷盆地扇形沉积体的分形几何特征与计算机模拟[D]. 武汉: 中国地质大学, 1998.24~25. [18] 张济忠. 分形[M]. 北京: 清华大学出版社, 1995. [19] 程极泰. 混沌的理论与应用[M]. 上海: 上海科学技术文献出版社, 1992.1~32. [20] 张卢侃, 孙建华. 混沌动力学[M]. 上海: 上海翻译出版公司, 1990.1~156. [21] 吴冲龙, 张洪年, 周江羽. 盆地模拟的系统观与方法论[J]. 地球科学——中国地质大学学报, 1993, 18(6): 741~747. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX199306009.htm [22] 曾文曲, 王向阳. 分形的计算机模拟[M]. 沈阳: 东北大学出版社, 1993. [23] Emanuel A S, Alameda G K. Reservoir performance prediction methods based on fractal geostatistics[J]. SPE Reservoir Engineering, 1989, 4(3): 311~318. doi: 10.2118/16971-PA [24] Yngve Aasum, Kelkar M G. An application of geostatistics and fractal geometry for reservoir characterization [J]. SPE Formation Evaluation, 1991, 6(1): 11~19. doi: 10.2118/20257-PA [25] 林克湘, 张昌民, 雷卞军, 等. 地面—地下对比建立储层精细地质模型[M]. 北京: 石油工业出版社, 1995. [26] Scholz C H, Mandelbrot B B. 地球科学中的分形研究[M]. 刘祖荫, 皇甫岗, 崔增林译. 合肥: 中国科学技术出版社, 1991. -
下载:
点击查看大图
图(5)
计量
- 文章访问数: 3948
- HTML全文浏览量: 670
- PDF下载量: 13
- 被引次数: 0
