Characteristics of Global Great Earthquakes
-
摘要: 分析了全球、环太平洋地震带(P系)和低纬度环球剪切带(E系)的地震活动特征, 并运用小波变换技术对地震活动周期成分进行了定量研究, 结果表明: (1)全球地震活动存在45.5 a和32.0 a的显著周期成分, P系为45.5 a, E系为30.9 a和47.5 a; (2)全球及两大构造系7.0级以上地震频度均显示30.0 a左右的周期特征, 但地震频度与全球8.5级以上特大地震活动是不同步的, 不能作为判定地震活跃期与平静期的依据, 频度变化可能反映全球尺度的某种活动对地震产生的影响; (3)全球地震具有50.0 a尺度的活跃期与平静期; 当前全球地震活动处于2004年开始的以8.5级以上地震活动为特点的大释放阶段, 这种状态还将持续数年; E系处于Mw≥7.8大震活跃期的尾声, 而2010年智利Mw=8.8地震可能标志着P系开始进入大释放阶段.Abstract: Using the global earthquake catalogue with Mw≥7.0 since 1900, we analyze the characteristics of great earthquakes in the global area, the circum-Pacific seismic belt (namely P-system)and the low-latitude circum-earth zone (namely E-systerm) respectively. In addition, the technique of Morlet wavelet transform is applied to quantitatively analyze the seismicity periodicities. Results show: (1) there are two principal periodic components, including 45.5 a and 32.0 a, in the global seismicity. For the P-system, the principal period is 45.5 a. The principal periodic components are 30.9 a and 47.5 a in the seismicity of the E-system; (2) The earthquake frequency with Mw≥7.0 of the globe, the P-system and the E-system show a prominent period of about 30 a. However, the temporal process of earthquake frequency is not synchronous with the global seismicity of Mw≥8.5, so it is not properly distinguish the active or quiet period by frequency and the variation of earthquake frequency may be a reaction that some global activity influence on the global seismicity; (3) The global great earthquakes showing the seismicity period is about 50.0 a (including an active and a quiet period). Great earthquakes (Mw≥8.5) in globe occurred frequently since 2004, showing a high actively trend based on the characteristics of great earthquakes cyclic process. It has been in high active period with many large earthquakes(Mw≥7.8) in the E-system since 1992, and currently it is in the end of the active period. The 2010 Chile Mw=8.8 event may be the sign that it begins a new active period in the P-system.
-
图 2 全球7.0级以上地震年频度(a)、累积频度(b)、累积Benioff应变(c)(10 a窗长, 1 a滑动)及8.0级以上地震活动M-t图(d)
Fig. 2. Curves of the annual global Mw≥7.0 earthquake frequency (a), the cumulative frequency (b), the cumulative strain release (c) (the time window is 10 a and the time step is 1 a) and M-t chart of Mw≥8.0 (d)
图 3 全球7.0级以上地震累积频度与应变释放归一化处理后的结果
Fig. 3. Normalization for cumulative frequency and strain release of global earthquakes with Mw≥7.0
图 4 全球7.0级以上地震年Benioff应变周期谱分析
a.Benioff应变小波功率谱；b.Benioff应变显著周期谱(红线、绿线分别为95%、90%置信度检验)
Fig. 4. Periodic spectrum of the annual global earthquake Benioff-strain with Mw≥7.0
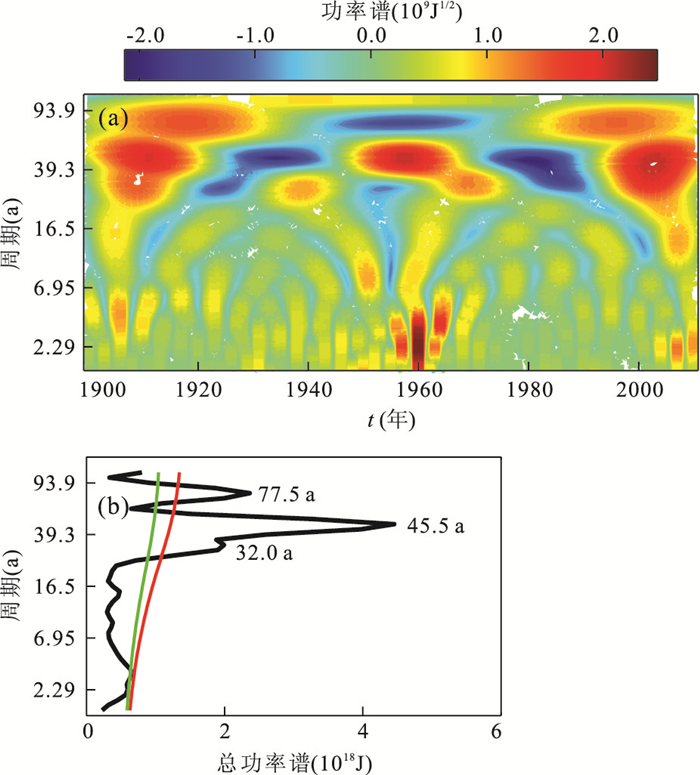
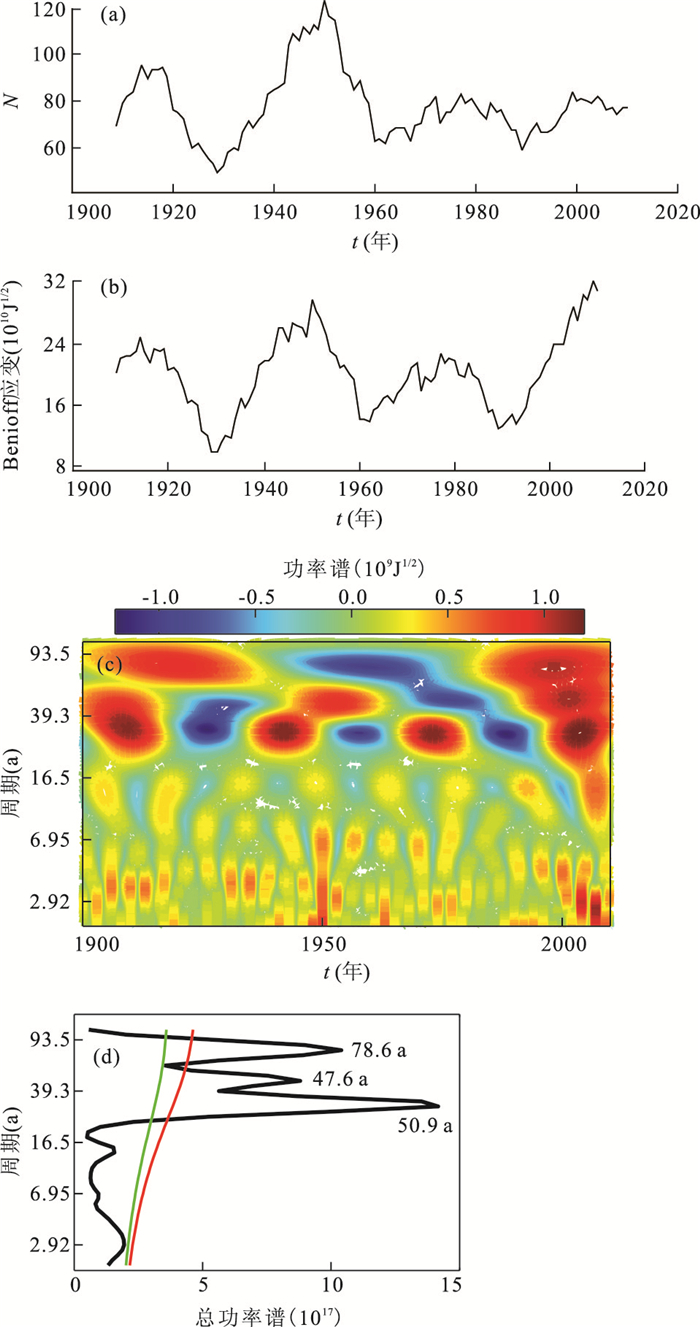
图 5 P系7.0级以上地震10 a累积频度图(a)、累积Benioff应变曲线(b)、小波功率谱(c)及显著周期谱(d)
图 6d中的红色、绿色线分别为95%、90%置信度检验
Fig. 5. Cumulative frequency (a) and Benioff-strain (b) with Mw≥7.0 of the P-system, periodic spectrum of the annual global earthquake Benioff-strain (c) and the predominant periods (d)
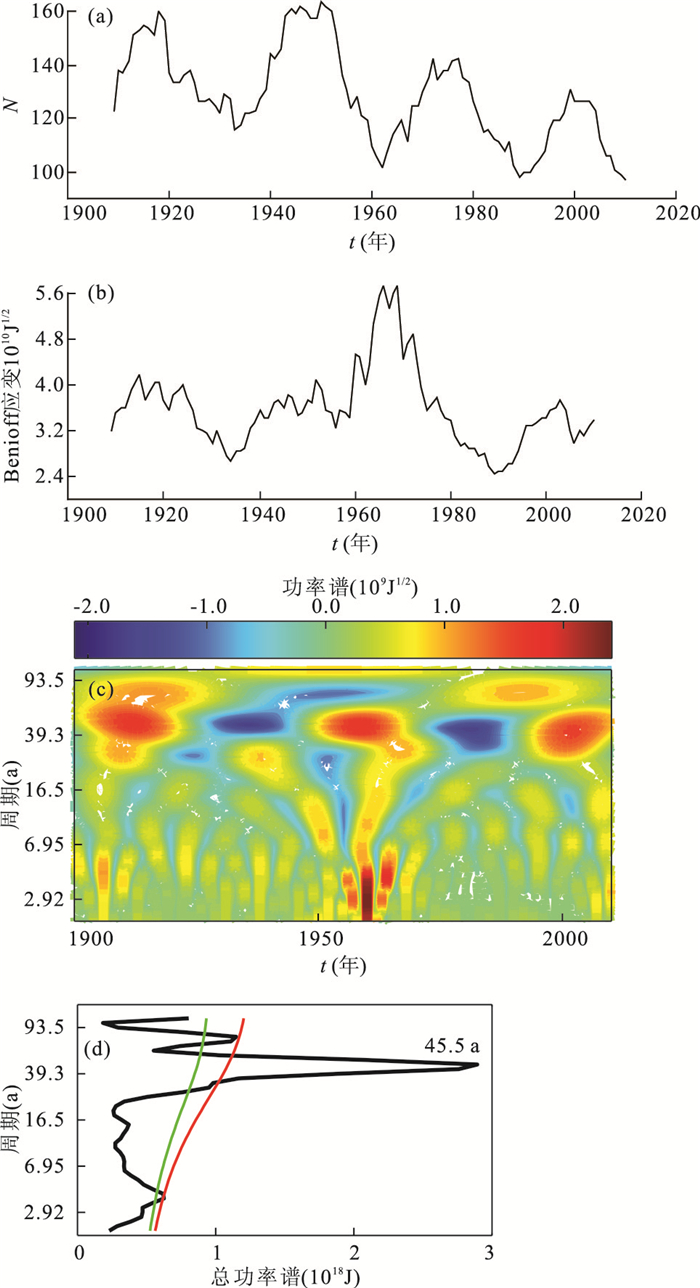
图 6 E系7.0级以上地震10年累积频度(a)、累积Benioff应变(b)、小波功率谱(c)及显著周期谱(d)
图 6d中的红色、绿色线分别为95%、90%置信度检验
Fig. 6. Cumulative frequency (a), Benioff-strain (b) with Mw≥7.0 of the E-system, periodic spectrum (c) and the predominant periods (d)
图 7 全球、P系及E系7.0级以上地震累积频度(a)和Benioff应变(b)归一化结果
Fig. 7. Normalization for cumulative frequency (a) and Benioff-strain (b) of global, the P-system and the E-system earthquakes with Mw≥7.0
-
Bai, C.H., Xu, W.Y., 2010. Multi-decadal to centennial secular variation of the main geomagnetic field. Chinese Journal of Geophysics, 53(4): 904-911(in Chinese with English abstract). doi: 10.3969/j.issn.0001-5733.2010.04.015 Bercovici, D., 1995. On the purpose of toroidal motion in a convecting mantle. Geophys. Res. Lett., 22: 3107-3110. doi: 10.1029/95GL03082 Ding, N., Guan, L.X., Wen, C.B., 2005. Study on fault signal of compressor with Morlet wavelet. Electrical Automation, 28(4): 7-10 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-YSJJ200504004.htm Du, P.R., Ma, Z.J., Gao, X.L., 2010. An analysis on episodes of great earthquakes in the low-latitude circum-earth zone and circum Pacific zone. Chinese Journal of Geophysics, 53(12): 2869-2874. doi: 10.3969/j.issn.0001-5733.2010.12.010 Engdahl, E.R., Villaseor, A., 2002. Global Seismicity: 1900-1999. In: Lee, W.H.K., Kanamori, H., Jennings, P.C., eds., International handbook of earth-quake and engineering seismology. Academic Press, San Diego, Part A: 665-690. Fan, H.S., 2001. A preliminary analysis of global seismicity since 1900. Recent Development in World Seismology, (2): 12-17 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GJZT200102002.htm Fedotov, S.A., 1965. On distribution patterns for strong earthquakes in Kamchatka, the Kurile Islands and northeastern Japan. Trudy Inst Fiz Zemli Akad, Nauk SSSR, 36: 66-93. Fedotov, S.A., 1968. The seismic cycle, quantitative seismic zoning, and long-term seismic forecasting. In: Medvedev S, V., ed., Seismic zoning in the USSR. Izdatel'stvo Nauka, Moscow, 133-166. He, L.S., Li, W.H., 2002. Morlet wavelet and its application in enveloping. Journal of Vibration Engineering, 15(1): 119-122 (in Chinese with English abstract). http://www.zhangqiaokeyan.com/academic-journal-cn_journal-vibration-engineering_thesis/0201213296397.html Kananmori, H., 1977. The energy release in great earthquakes. J. Geophys. Res., 82: 2981-2987. doi: 10.1029/JB082i020p02981 Lin, Z.S., Deng, Z.W., 1999. Study on diagnosis technology of wavelet climate. Seismological Press, Beijing (in Chinese). Ma, H.S., Zhou, L.Q., Shao, Z.G., et al., 2010. Process and trend of large earthquakes on the earth and in the China continent and its surroundings. Earthquake, 30(2): 29-37 (in Chinese with English abstract). http://www.researchgate.net/publication/289266678_Process_and_trend_of_large_earthquakes_on_the_earth_and_in_the_China_continent_and_its_surroundings Ma, Z.J., Jiang, M., 1987. Strong earthquake period and episodes in China. Earthquake Research in China, 3(1): 47-51. http://en.cnki.com.cn/Article_en/ http://search.cnki.net/down/default.aspx?filename=ZGZD198701007&dbcode=CJFD&year=1987&dflag=pdfdown Ma, Z.J., Du, P.R., Ren, J.W., et al., 2006. Eposodes of great earthquakes in the low-latitude circum-earth zone and circum Pacitic zone. Science in China (Ser. D), 36(4): 326-331 (in Chinese with English abstract). http://www.researchgate.net/publication/289266760_An_analysis_on_episodes_of_great_earthquakes_in_the_low-latitude_circum-earth_zone_and_circum_Pacific_zone Mallat, S., 1991. Zero-crossings of a wavelet transform. IEEE Transaction on Information Theory, 37(4): 1019-1033. doi: 10.1109/18.86995 Mei, S.R., 1960. Seismic activity in China. Acta Geophysica Sinica, 9(1): 1-19 (in Chinese with English abstract). Mogi, K., 1974. Active periods in the world's chief seismic belts. Tectonophysics, 22: 265-282. doi: 10.1016/0040-1951(74)90086-9 Mogi, K., 1979. Global variation of seismic activity. Tectonophysics, 57: 43-50. doi: 10.1016/0040-1951(79)90142-2 Torrenee, C., Compo, G.P., 1998. A practical guide to wavelet analysis. Bull Amer. Meteor Soc., 79(1): 61-78. doi: 10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 Wells, D.L., Coppersmith, K.J., 1994. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Geol. Soc. Am., 84(4): 974-1002. http://gji.oxfordjournals.org/cgi/ijlink?linkType=ABST&journalCode=ssabull&resid=84/4/974 Xu, D.Y., Zheng, W.Z., An, Z.S., 1980. Heavenly spheres and earthquake prediction. Seismological Press, Beijing (in Chinese). Yin, J.Y., Zhu, Y.Q., Song, Z.P., 2011. Significance test and precision analysis of Morlet wavelet: application to studying periodic variation of earthquake activity and geomagnetic field. Acta Seismologica Sinica, 33(5): 663-671 (in Chinese with English abstract). http://d.wanfangdata.com.cn/periodical/dizhen201105010 Yu, Y., Hong, H.J., Liu, P.X., et al., 2003. Spatiotemporal distribution of global great earthquakes and dynamic mechanism. Earth Science Frontiers, 10(Special): 5-10 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DXQY2003S1002.htm 白春华, 徐文耀, 2010. 主磁场长期变化十年至百年尺度的周期. 地球物理学报, 53(4): 904-911. doi: 10.3969/j.issn.0001-5733.2010.04.015 丁娜, 关立行, 文常保, 2005. Morlet小波对于压缩机故障信号的研究. 电气自动化, 28(4): 7-10. https://www.cnki.com.cn/Article/CJFDTOTAL-DQZD200604020.htm 杜品仁, 马宗晋, 高祥林, 2010. 低纬度环球带和环太平洋带大地震的幕式活动分析, 地球物理学报, 53(12): 2869-2874. doi: 10.3969/j.issn.0001-5733.2010.12.010 范洪顺, 2001.1900年以来全球地震活动的初步分析. 国际地震动态, (2): 12-17. https://www.cnki.com.cn/Article/CJFDTOTAL-GJZT200102002.htm 何岭松, 李巍华, 2002. 用Morlet小波进行包络检波分析. 振动工程学报, 15(1): 119-122. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC200201024.htm 林振山, 邓自旺, 1999. 子波气候诊断技术的研究. 北京: 气象出版社. 马宏生, 周龙泉, 邵志刚, 等, 2010. 全球及中国大陆周边强震活动状态研究. 地震, 30(2): 29-37. https://www.cnki.com.cn/Article/CJFDTOTAL-DIZN201002004.htm 马宗晋, 杜品仁, 任金卫, 等, 2006. 低纬度环球剪切带及其与环太平洋带大地震的幕式活动. 中国科学(D辑), 36(4): 326-331. https://www.cnki.com.cn/Article/CJFDTOTAL-JDXK200604002.htm 梅世蓉, 1960. 中国的地震活动性. 地球物理学报, 9(1): 1-19. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX196001000.htm 徐道一, 郑文振, 安振声, 1980. 天体运行与地震预报. 北京: 地震出版社. 尹继尧, 朱元清, 宋治平, 等, 2011. Morlet小波显著性检验和精度分析在地磁场和地震活动性周期分析中的应用. 地震学报, 33(5): 663-671. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB201105012.htm 于泳, 洪汉净, 刘培洵, 等, 2003. 全球大地震时空分布与动力学机制的初步研究. 地学前缘(特刊), 10: 5-10. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY2003S1002.htm -
下载:
点击查看大图
计量
- 文章访问数: 3624
- HTML全文浏览量: 769
- PDF下载量: 99
- 被引次数: 0
