Effects on Seismic Velocity of Post-Perovskite MgSiO3 under Hydrostatic and Uniaxial Pressure
-
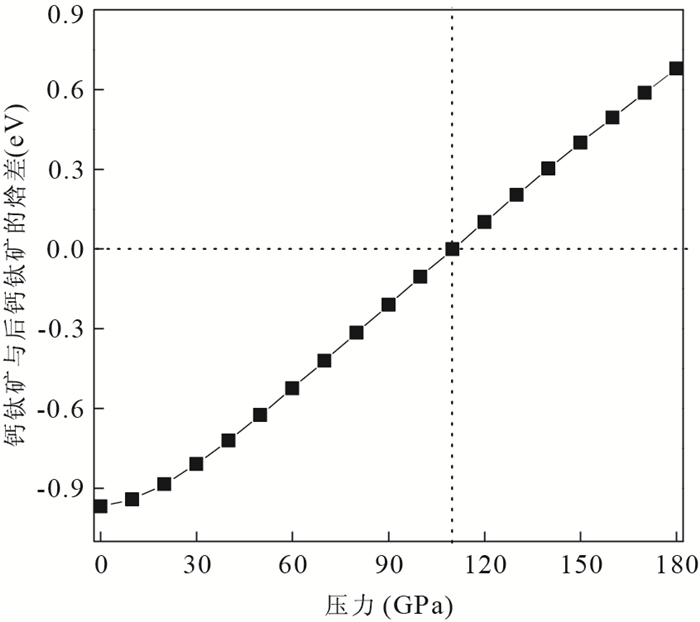
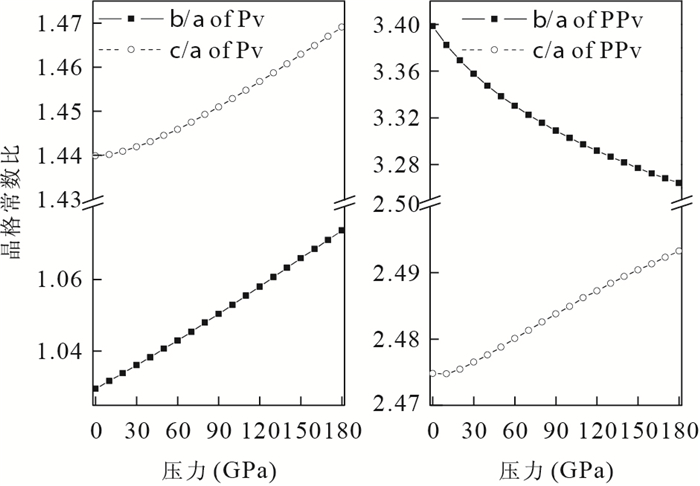
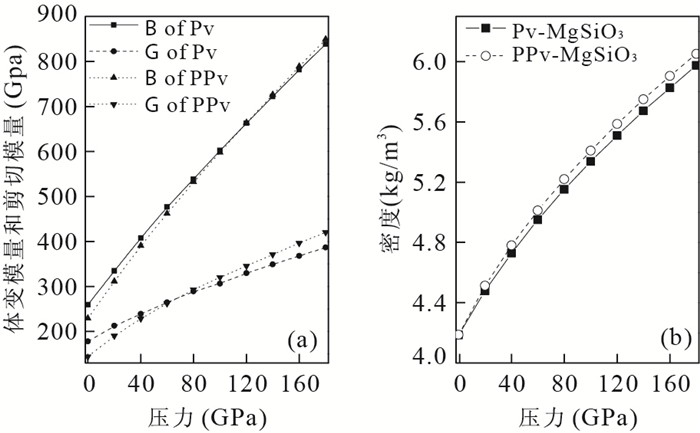
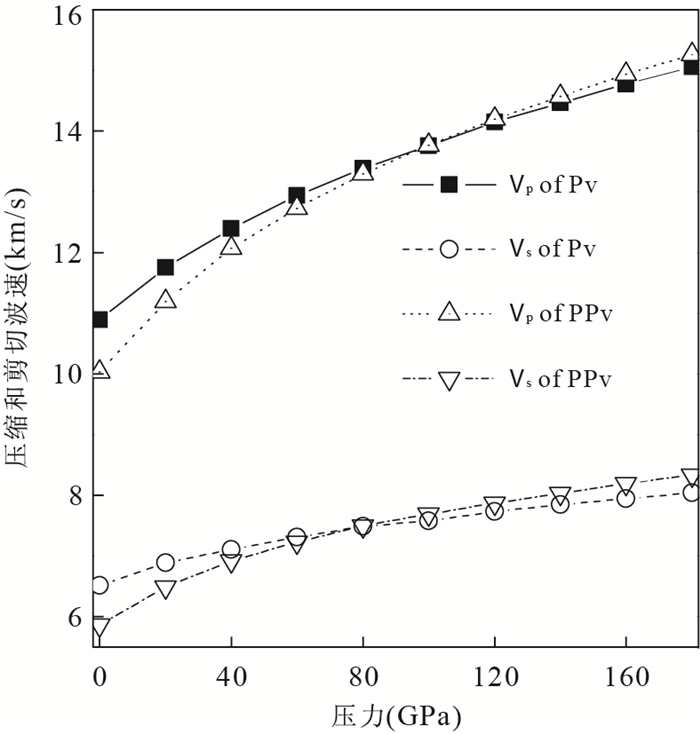
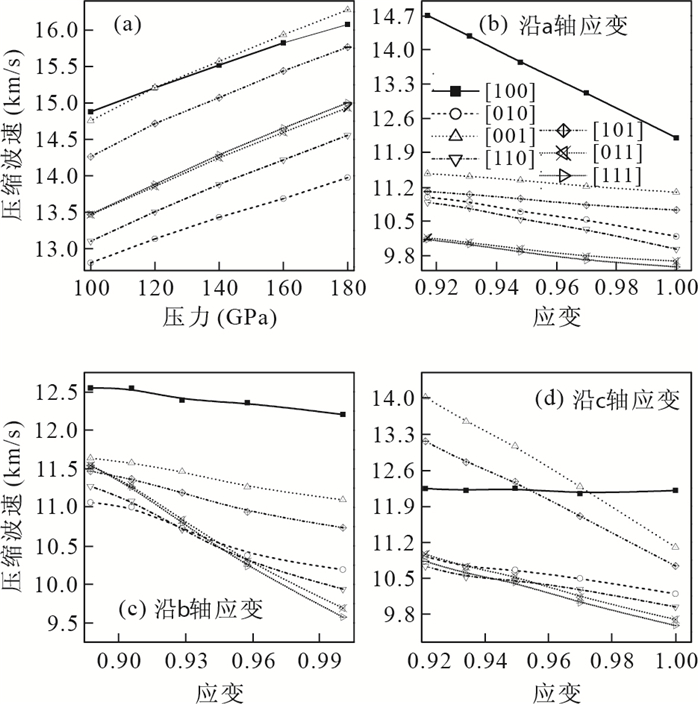
摘要: 后钙钛矿MgSiO3对于重新认识地球的基本结构和成分具有重大意义.采用基于密度泛函理论的第一性原理计算对后钙钛矿MgSiO3在静水压力和单轴压力下的弹性性质和地震波速特征进行了研究.首先通过总能比较和力学稳定性判据验证了后钙钛矿MgSiO3在高压下的稳定性, 并且计算得到的晶格常数与前人结果符合很好.计算表明在高压下(D"层), 后钙钛矿具有比钙钛矿大的体变模量、剪切模量及密度, 并且具有大的地震波速, 这与地震观测D"层中地震波速的不连续性一致.在静水压力作用下, 计算结果显示压缩波各向异性基本保持不变, 而剪切波各向异性增强.有单轴应力作用时, 后钙钛矿地震波各向异性差异非常明显, 当压力作用在a轴或c轴上时, 能够得到比对应静水压力下后钙钛矿更强的各向异性, 而恰好相反的是, 压缩b轴时, 各向异性有减小的趋势.本研究能为解释地幔底部地震波不连续性和横向差异提供一定的参考.Abstract: The elastic property and seismic velocity of Post-Perovsikt (PPv) MgSiO3 have been studied using first-principles calculations based on density of functional theory (DFT).Firstly, the stability of PPv-MgSiO3 under high pressure is validated through total energy calculations and the criterion of mechanical stability.The obtained lattice constants are in accordance well with the previous calculated and experimental results.The calculations indicate that the bulk modulus, shear modulus, density and seismic velocity of PPv-MgSiO3 are larger than those of Pv-MgSiO3, which are in agreement with seismic observations.Under hydrostatic pressure, the anisotropy of compressed wave has little change, while that of shear wave is enhanced.For the uniaxial pressure, both compressed and shear anisotropies are increased with strain along the a or c axis, while are decreased with strain along the b axis with respect to that of hydrostatic pressure.This study is useful for explaining the seismic velocity discontinuity and lateral heterogeneity in the D" layer.
-
Key words:
- Post-Perovskite MgSiO3 /
- hydrostatic pressure /
- uniaxial pressure /
- D" layer /
- seismic velocity /
- mineral materials
-
后钙钛矿MgSiO3(Post-Perovskite MgSiO3，PPv-MgSiO3)对于重新认识地球的基本结构和成分具有重大意义，被认为是21世纪初地球深部研究最重大的发现.人们期望通过此新的高温高压相矿物解释地震波位于核幔边界上方的D"层内的独特特征.其主要特征包含以下几个方面：(1)不连续性.核幔边界上方200~300 km范围内，压缩波(P波)和剪切波(S波)波速比D"层上方波速都有约3%的增加；(2)强烈的不均匀性.地幔底部的300 km横向不均匀性明显增强，全球速度模型在D"层内的S波速度异常变化约为±2%~4%，P波速度异常约为±1%(Gu et al., 2001; Kárason and van der Hilst，2001; Zhao，2001; Grand，2002)；(3)强的各向异性.D"层高质量的反射、折射和绕射数据分析表明D"层中的S波分裂普遍存在，如环大平洋区域，水平极化的S波要比垂直极化的S波快1%~3%(张中杰，2002; 杨凤琴等，2008)；(4)存在超低声速区(ultra low velocity zone，ULVZ).位于D"层下部核幔边界5~60 km之间，P波速度减小5%~10%，而S波速度减小可达10%~30%，并且密度增加可达10%(Garnero and Helmberger, 1995; Wen and Helmberger, 1998; Vidale and Hedlin, 1998; Ni and Helmberger, 2003).D"层在地球动力学上有重大意义，因而理解和解释该层的地震波特征一直是地震学和相关学科的研究热点(朱介寿，2000; Murakami et al., 2004; 候渭等，2005; 唐群署和李丽红，2006; Rost et al., 2010; 张苑和舒良树，2010).不过，由于其自身的复杂性，迄今对地震波的异常传播特征仍存在较大争议.综合目前成果来看，形成D"层的地震波特征应该是多方面的，可能是包含局部融熔体、化学不均匀性等，最近又提出了D"层中伴随有相变产生.因此，要揭示D"层地震波特征的本质仍需要各个学科继续共同努力.
2004年以来，多个研究组从模拟计算和实验分别证实了在D"层条件下，钙钛矿MgSiO3(Perovskite MgSiO3，Pv-MgSiO3)会相变成PPv-MgSiO3(Iitaka et al., 2004; Mao et al., 2004; Murakami et al., 2004; Oganov and Ono, 2004; Shim et al., 2004).该相变能引起1%~2%的地震波速度和1%左右的密度增加，并且还可以引起可观的各向异性，从而提供了新的机制来解释地震学在D"层的观测结果(Garnero et al., 2004；Wookey et al., 2005).
由于PPv-MgSiO3发现的时间较短，并且相变在实验上很难控制，加之极端条件下测量PPv-MgSiO3的性质很难，人们对其在D"层条件下的性质的认识还不充分.因此借助基于量子力学的第一性原理计算模拟方法是研究和理解此区领域的有力方法.到目前为止，此方法已被成功应用于研究镁橄榄石(Liu et al., 2009)和Pv-MgSiO3的性质(Li et al., 2005; Stackhouse et al., 2006; Zhang and Oganov, 2006; Bengtson et al., 2008; Caracas et al., 2010; Hsu et al., 2010).利用第一性原理计算方法，预测了Pv-MgSiO3向PPv-MgSiO3的相变，有些工作得到了与实验符合较好的结果，并且一定程度上能够证实在这个区域内的地震学或地球动力学结论.在这些计算工作中，都考虑到了静水压对地震波速及其各向异性的影响.在复杂的地球内部，可能会存在各轴上压力相差比较大的情况，此时PPv-MgSiO3的地震波速和各向异性又会发生怎样的变化呢? 因此本文将采用基于量子力学的第一性原理计算方法，比较研究在静水压力和单轴压力下地震波速和各向异性的特征.
1. 计算模型及方法
PPv-MgSiO3为底心正交结构，空间群为Cmcm，其晶胞如图 1所示：沿c轴方向在SiO6八面体顶角位置的氧原子相连接，沿a轴方向由SiO6八面体两边相连形成链状连接，这种SiO6八面体的链沿b轴形成层状堆积，Mg2+阳离子位于SiO6八面体的层状堆积之间.本文计算采用基于密度泛函理论(density functional theory，DFT)的平面波赝势方法的CASTEP软件.电子与离子核间的相互作用用超软赝势来描述(Perdew and Zunger, 1981)，交换关联相互作用采用局域密度近似(LDA)(Vanderbilt，1990).为确保计算能满足足够的精度，本文计算平面波截断能均取为1.282×10-16 J，系统总能量和电荷密度在布里渊区的积分计算使用Monkhorst-Pack方案(Monkhorst and Pack, 1976)来选择k空间网格点(Pv-MgSiO3和PPv-MgSiO3分别取为10×10×4和18×6×8)，保证了体系能量和构型在准完备基上的收敛.原子间的相互作用收敛标准为1.602×10-11 J/m，每原子的能量收敛标准为8.01×10-25 J.
2. 结果与讨论
2.1 高压下的晶格常数与弹性性质
首先对PPv-MgSiO3在0~180 GPa范围内的结构进行了优化，为了便于比较，对Pv-MgSiO3也进行了计算.图 2给出了2种结构的焓差值随压强的变化关系.可以看出当压力高于110 GPa时，Pv-MgSiO3的焓要高于PPv-MgSiO3，说明在高压下PPv-MgSiO3要比Pv-MgSiO3结构更加稳定，相变可能在此压强附近发生.前人的计算工作(Shim et al., 2004)给出了120 GPa时PPv-MgSiO3的晶格常数为a=2.456×10-10 m、b=8.042×10-10 m和c=6.093×10-10 m，实验在121 GPa，300 K条件下测得的晶格常数分别为a=2.455×10-10 m、b=8.051×10-10 m和c=6.099×10-10 m，本文计算得到的120 GPa时晶格常数为a=2.440×10-10 m、b=8.031×10-10 m和c=6.068×10-10 m.可以看出本文计算结果与前人的计算结果和实验值符合得很好.
图 2 Pv-与PPv-MgSiO3的焓差值(ΔH)与压力(P)的关系Fig. 2. Difference of enthalpy between Pv- and PPv-MgSiO3在静水压力作用下，两种结构晶格常数比率(b/a和c/a)变化情形如图 3所示.很明显两种结构的压缩性质存在较大的差异，PPv结构压缩时各向异性要强于Pv-MgSiO3.Pv-MgSiO3在压力作用下，b/a和c/a同时增大，表明a轴最容易被压缩.在较低压力时，c/a变化较为平缓，随着压力的增加趋近线性变化；而b/a始终接近线性变化，并且线性变化的斜率与c/a在高压时的斜率趋于一致，说明在较高压强时，b轴与c轴具有相近的压缩性质.对于PPv-MgSiO3，b/a随压力减小，而c/a随压力增加，因此3轴中，b轴最容易被压缩，而c轴最难以被压缩，这与其他研究中认为b轴方向为晶格优选方向一致(Tsuchiya et al., 2004).两种结构间不同的压缩特性，必然导致它们间弹性常数的差异.
图 3 Pv-与PPv-MgSiO3中晶格常数比值(b/a，c/a)与压力(P)的关系Fig. 3. Pressure dependence of b/a and c/a of Pv- and PPv-MgSiO3表 1中列出了PPv-MgSiO3在不同压力下的弹性常数.从表中可以看出PPv-MgSiO3有着较强的各向异性，并且9个独立的弹性常数都随着压力的增加而增大，各向异性增强.在所有压力下，3个压缩弹性常数中C11和C33很接近，且都比C22要大一些，这也验证了前面提到的b轴最容易被压缩的事实.剪切弹性常数中虽然都在随压力增加而增大，但是可以看出C66在0 GPa时(此条件下Pv-MgSiO3更稳定)要小于C44和C55，但在高压下，明显增加很快，其值超过了C44和C55，说明晶体在高压作用下侧向偏移性质在发生剧烈的改变.PPv-MgSiO3属正交晶系，可以利用正交晶系的力学稳定性判据来验证其在高压下的结构稳定性.正交晶系的力学稳定性判据为：
C11>0,C22>0,C33>0,C44>0,C55>0,C66>0,C11+C22+C33+2C12+2C13+2C23>0,C11+C22−2C12>0,C11+C33−2C13>0,C22+C33−2C23>0, 表 1 PPv-MgSiO3在不同压力下(P)的弹性常数(单位：GPa)Table Supplementary Table Elastic constants of PPv-MgSiO3 under different pressure (in GPa)P C11 C22 C33 C44 C55 C66 C12 C13 C23 0 624 435 516 100 134 96 49 84 119 120 1 290 962 1 290 300 286 415 418 325 487 160 1 475 1 103 1 496 352 331 504 521 402 593 由表中所列弹性常数可知PPv-MgSiO3在高压下是满足力学稳定性的，也进一步证实了“Pv→PPv”相变的产生.
图 4(a)给出了Pv-和PPv-MgSiO3在高压作用下体变模量和剪切模量的变化.从图中可以看出，压力较低时，Pv-MgSiO3的体变模量和剪切模量均要大于PPv-MgSiO3.随着压力的增大，PPv-MgSiO3的体变模量和剪切模量增加较快，在一定压强后，会比Pv-MgSiO3的要大.压缩声速(纵波，Vp)和剪切声速(横波，Vs)分别由Vp=√(B+4G/3)/ρ和Vs=√G/ρ给出，因此两种结构的体变模量和剪切模量的差异会造成地震波速的差异.Pv-和PPv-MgSiO3在高压下的密度变化如图 4b所示，可以看出，在本文所计算的压力范围内，PPv-MgSiO3的密度均大于Pv-MgSiO3，因此也可以说明实验发现的Pv-MgSiO3在高压下密度增加，即是由Pv→PPv相变引起的.两种结构的体相波速如图 5所示：低压力时，PPv-MgSiO3的Vp和Vs都要低于Pv-MgSiO3，而在压力较高时，PPv-MgSiO3的Vp和Vs均大于Pv-MgSiO3.在PPv-MgSiO3能够稳定存在的D"层中，压强可以达到125~135 GPa，因此可以解释在此区域内，速度要大于其他以Pv-MgSiO3形式存在的区域.
图 4 体变模量(B)，剪切模量(G)及密度(D)与静水压力(P)的关系Fig. 4. Pressure dependence of bulk modulus, shear modulus and density
图 5 Pv-与PPv-MgSiO3中波速(V)与压力(P)关系Fig. 5. Pressure dependence of seismic velocity of Pv- and PPv-MgSiO3如前所述，地幔底部的300 km横向不均匀性明显增强，全球速度模型在D"层内的S波速度异常变化约为±2%~4%，P波速度异常约为±1%.在复杂的地球系统内部，PPv-MgSiO3各方向上受到的压力可能相差较大，并且可能产生不同于静水压力情形下的地震波特征，借此来为解释这种横向不均匀性提供一种参考，因此本文研究了单轴压力作用下PPv-MgSiO3的弹性性质和地震波速特征.文中计算时单轴压力是通过改变晶格单轴的晶格长度来实现的，并且对晶格长度改变后的晶格中离子的位置进行了优化.图 6给出了PPv-MgSiO3在单轴压力作用下体变模量和剪切模量的变化情况.图中的各点为计算值，线为拟合.从图中可以反映出，体变模量和剪切模量在单轴应力作用下基本上呈现出线性变化，但是在不同轴上变化差异较大.沿a轴施加压力时，体变模量和剪切模量的斜率最小；而当压力施加在c轴时，体变模量和剪切模量分别对应最大斜率.这种不规律的变化会引起异于静水压力作用下的各向异性.因此单轴压力施加在不同的轴上时，地震波速和其各向异性会发生强烈的变化.
图 6 体变模量(B)和剪切模量(G)与单轴压力的关系Fig. 6. Uniaxial pressure dependence of bulk modulus and shear modulus2.2 地震波速各向异性
图 7给出了压缩波在静水压力和单轴压力作用下沿各方向的传播特征.在静水压力作用下，Vp最大值会由[100]方向变化到[001]方向，而最小的Vp始终处在[010]方向上.在单轴压力作用下，Vp表现出了与静水压下的不同特征.当a轴施加压力时，Vp沿[100]方向始终具有最大值，而最小值并不是静水压下的[010]方向，而是[111]方向，并且与[011]方向的速度非常接近.而当应力施加到b轴时，Vp最大值方向仍为[100]方向，在较小压力时，Vp最小值在[111]方向，但随着压力增加，[110]和[010]方向会相继成为Vp最小值方向.当c轴上施加压力时，有一个非常有趣的现象，沿[100]方向的波速基本上保持不变.施加压力较小时，Vp在[100]方向有最大值，而后[001]方向为最大值.最小值方向也发生了转变，压力较小时，速度最小值在[111]方向，而压力较大时变为[110]方向.剪切波速也有类似的转变.
图 7 PPv-MgSiO3中不同传播方向压缩波波速与压力(应变)的关系Fig. 7. Hydrostatic and uniaxial pressures dependence of seismic velocities of different directions地震波速各向异性的定义式为：A=(Vmax-Vmin)/〈V〉×100%，其中Vmax和Vmin分别代表压缩和剪切最大和最小速度，〈V〉为等向平均值.表 2给出了PPv-MgSiO3分别在静水压力下和单轴压力下的各向异性.在静水压力作用下，因为各方向压缩波的变化都接近斜率相同的线性变化，因此其各向异性(Ap)基本保持不变，而剪切波各向异性(As)增强.在单轴压力作用下(表中所列a/a0、b/b0和c/c0分别为静水压力在100 GPa和180 GPa时对应的晶格常数与零压下晶格常数的比率)，各向异性呈现出了丰富的变化.压力作用在a轴时，各向异性变化较为明显，特别是Ap，当a为180 GPa下的晶格常数时，其达到了41%；As也有随着压力的增加而增强的趋势.当压力作用在b轴时，恰好和在a轴施加压力时相反，此时Ap和As都会比对应静水压力下的各向异性要低，也就是b轴的压缩有利于减小各向异性.施加在c轴上时现象和在a轴上类似，均比对应静水压力时的各向异性要高一些，而且随着压力的增大，Ap和As都在增加.
表 2 PPv-MgSiO3中在压力下的压缩波(Ap)和剪切波(As)的各向异性Table Supplementary Table Anisotropies of seismic velocities of PPv-MgSiO3 under pressureAp As 静水压力 100 GPa 15.1% 17.6% 180 GPa 15.1% 23.6% 单轴压力 a/a0=0.907 6 15.65% 19.84% a/a0=0.877 0 40.97% 28.73% b/b0=0.876 0 14.62% 9.5% b/b0=0.836 0 13.63% 17.77% c/c0=0.910 4 27.11% 26.52% c/c0=0.882 0 29.97% 31.93% 3. 结论
采用第一性原理计算研究了PPv-MgSiO3在高压下(D"层，静水压力和单轴压力)的弹性性质和地震波速特征.首先通过计算Pv-和PPv-MgSiO3两种结构的总能及正交晶系的力学稳定性判据验证了PPv-MgSiO3在高压下的稳定性，得到的晶格常数与前人的实验值和计算结果符合得很好.在静水压力的作用下，PPv结构的晶格常数比率(b/a，c/a)呈现出比Pv结构更复杂的变化；计算得到的弹性常数在各方向的差异较大，并且随压力变化明显，上述两方面都揭示出PPv-MgSiO3具有较大的各向异性.计算得到了地震波速随静水压和单轴压力作用下的变化情况，在高压作用下，PPv-MgSiO3的地震波速要大于Pv-MgSiO3，符合地震观测现象.在静水压力和单轴压力的作用下，地震波最大和最小速度方向都有可能会发生转变.最后分析了压力作用对地震波速各向异性的影响，在静水压力作用下，压缩波的各向异性基本保持不变，而剪切波各向异性增强.当单轴压力作用在a或c轴上时，能够得到增强的各向异性，而恰好相反，压缩b轴时，各向异性有减小的趋势.
-
图 2 Pv-与PPv-MgSiO3的焓差值(ΔH)与压力(P)的关系
Fig. 2. Difference of enthalpy between Pv- and PPv-MgSiO3
图 3 Pv-与PPv-MgSiO3中晶格常数比值(b/a，c/a)与压力(P)的关系
Fig. 3. Pressure dependence of b/a and c/a of Pv- and PPv-MgSiO3
图 4 体变模量(B)，剪切模量(G)及密度(D)与静水压力(P)的关系
Fig. 4. Pressure dependence of bulk modulus, shear modulus and density
图 5 Pv-与PPv-MgSiO3中波速(V)与压力(P)关系
Fig. 5. Pressure dependence of seismic velocity of Pv- and PPv-MgSiO3
图 6 体变模量(B)和剪切模量(G)与单轴压力的关系
Fig. 6. Uniaxial pressure dependence of bulk modulus and shear modulus
图 7 PPv-MgSiO3中不同传播方向压缩波波速与压力(应变)的关系
Fig. 7. Hydrostatic and uniaxial pressures dependence of seismic velocities of different directions
表 1 PPv-MgSiO3在不同压力下(P)的弹性常数(单位：GPa)
Table 1. Elastic constants of PPv-MgSiO3 under different pressure (in GPa)
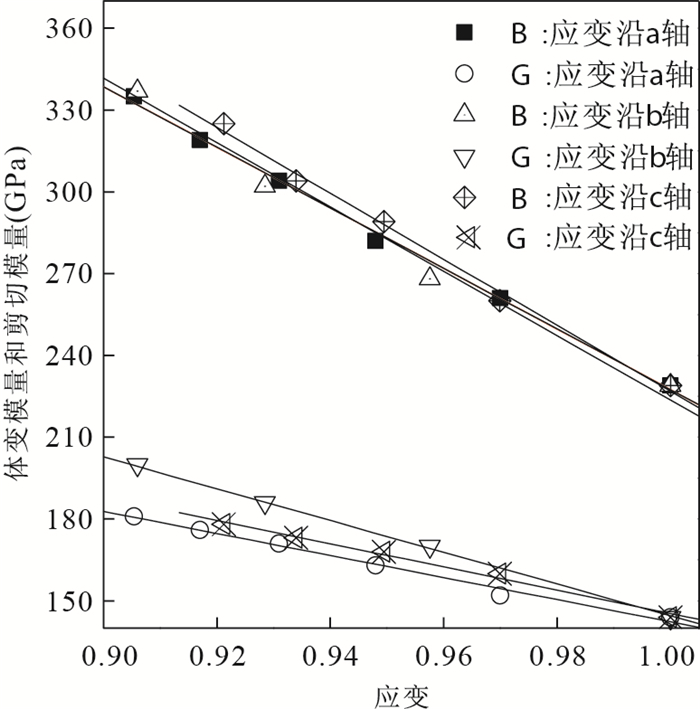
P C11 C22 C33 C44 C55 C66 C12 C13 C23 0 624 435 516 100 134 96 49 84 119 120 1 290 962 1 290 300 286 415 418 325 487 160 1 475 1 103 1 496 352 331 504 521 402 593 
下载: 导出CSV
表 2 PPv-MgSiO3中在压力下的压缩波(Ap)和剪切波(As)的各向异性
Table 2. Anisotropies of seismic velocities of PPv-MgSiO3 under pressure
Ap As 静水压力 100 GPa 15.1% 17.6% 180 GPa 15.1% 23.6% 单轴压力 a/a0=0.907 6 15.65% 19.84% a/a0=0.877 0 40.97% 28.73% b/b0=0.876 0 14.62% 9.5% b/b0=0.836 0 13.63% 17.77% c/c0=0.910 4 27.11% 26.52% c/c0=0.882 0 29.97% 31.93%
下载: 导出CSV
-
Bengtson, A., Persson, K., Morgan, D., 2008. Ab Initio Study of the Composition Dependence of the Pressure-induced Spin Crossover in Perovskite (Mg1-x, Fex)SiO3. Earth Planet. Sci. Lett. , 265(3-4): 535-545. doi: 10.1016/j.epsl.2007.10.049 Caracas, R., Mainprice D., Thomas C., 2010. Is the Spin Transition in Fe2+-Bearing Perovskite Visible in Seismology? Geophys. Res. Lett. , 37(3): L133091- L133096. doi: 10.1029/2010GL043320 Garnero, E.J., Helmberger, D.V., 1995. A Very Slow Basal Layer Underlying Large-Scale Low-Velocity Anomalies in the Lower Mantle Beneath the Pacific: Evidence from Core Phases. Phys. Earth Planet. Int. , 91(1-3): 161-176. doi: 10.1016/0031-9201(95)03039-Y Garnero, E.J., Maupin, V., Lay, T., et al., 2004. Variable Azimuthal Anisotropy in Earth's Lowermost Mantle. Science, 306(5694): 259-261. doi: 10.1126/science.1103411 Grand, S.P., 2002. Mantle Shear-wave Tomography and the Fate of Subducted Slabs. Phil. Trans. R. Soc. Lond. A, 360(1800): 2475-491. doi: 10.1098/rsta.2002.1077 Gu, Y.J., Dziewonski, A.M., Su W.J., et al., 2001. Models of the Mantle Shear Velocity and Discontinuities in the Pattern of Lateral Heterogeneities. J. Geophys. Res. , 106(B6): 11169-11199. doi: 10.1029/2001JB000340 Hou, W., Xie, H.S., Zhou, W.G., 2005. Lowermost Mantle Layer and Its Significance in the Earth's Material Evolution. Earth-Science Frontiers, 12(1): 37-41 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-DXQY200501004.htm Hsu, H., Umemoto, K., Blaha, P., et al., 2010. Spin States and Hyperfine Interactions of Iron in (Mg, Fe)SiO3 Perovskite under Pressure. Earth Planet. Sci. Lett. , 294(1-2): 19-26. doi: 10.1016/j.epsl.2010.02.031 Iitaka, T., Hirose, K., Kawamura, K., et al., 2004. The Elasticity of the MgSiO3 Post-Perovskitep Phase in the Earth's Lowermost Mantle. Nature, 430(6998): 442-445. doi: 10.1038/nature02702 Kárason, H., van der Hilst, R.D., 2001. Tomographic Imaging of the Lowermost Mantle with Differential Times of Refracted and Diffracted Core Phases (PKP, Pdiff). J. Geophys. Res. , 106(B4): 6569-6587. doi: 10.1029/2000JB900380 Li, L., Brodholt, J.P., Stackhouse, S., et al., 2005. Electronic Spin State of Ferric Iron in Al-Bearing Perovskite in the Lower Mantle. Geophys. Res. Lett. , 32(17): L173071-L173074. doi: 10.1029/2005GL023045 Liu, L., Du, J.G., Zhao, J.J., et al., 2009. Elastic Properties of Hydrous Forsterites under High Pressure: First-principle Calculations. Phys. Earth Planet. Int. , 176(1-2): 89-97. doi: 10.1016/j.pepi.2009.04.004 Mao, W.L., Shen, G.Y., Prakapenka, V.B., et al., 2004. Ferromagnesian Post-Perovskite Silicates in the D" Layer of the Earth. Proc. Nat. Acad. Sci. , 101(45): 15867-15869. doi: 10.1073/pnas.0407135101 Monkhorst, H.J., Pack, J.D., 1976. Special Points for Brillouin-zone Integrations. Phys. Rev. B, 13(12): 5188-5192. doi: 10.1103/PhysRevB.13.5188 Murakami, M., Hirose, K., Kawamura, K., et al., 2004. Post-Perovskite Phase Transition in MgSiO3. Science, 304(5672): 855-858. doi: 10.1126/science.1095932 Ni, S.D., Helmberger, D.V., 2003. Seismological Constraints on the South African Superplume; Could Be the Oldest Distinct Structure on Earth. Earth Planet. Sci. Lett. , 206(1-2): 119-131. doi: 10.1016/S0012-821X(02)01072-5 Oganov, A.R., Ono, S., 2004. Theoretical and Experimental Evidence for A Post-Perovskite Phase of MgSiO3 in Earth's D" layer. Nature, 430(6998): 445-448. doi: 10.1038/nature02701 Perdew, J.P., Zunger, A., 1981. Self-interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B, 23(10): 5048-5079. doi: 10.1103/PhysRevB.23.5048 Rost, S., Garnero, E.J., Stefan W., 2010. Thin and Intermittent Ultralow-Velocity Zones. J. Geophys. Res. , 115(B6): B0631201-B0631212. doi: 10.1029/2009JB006981 Shim, S.H., Duffy, T.S., Jeanloz, R., et al., 2004. Stability and Crystal Structure of MgSiO3 Perovskite to the Core-mantle Boundary. Geophys. Res. Lett. , 31(10): L106031-L106035. doi: 10.1029/2004GL019639 Stackhouse, S., Brodolt, J.P., Dobson, D.P., et al., 2006. Electronic Spin Transitions and the Seismic Properties of Ferrous Iron-Bearing MgSiO3 Post-perovskite. Geophys. Res. Lett. , 33(12): L12S031- L12S034. doi: 10.1029/2005GL025589 Tang, Q.S., Li, L.H., 2006. The Earth's Lowermost Mantle and Its Seismological Research Progress. Earth Science Frontiers, 13(2): 213-223 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DXQY200602024.htm Tsuchiya, T., Tsuchiya, J., Umemoto, K., et al., 2004. Elasticity of Post-Perovskite MgSiO3. Geophys. Res. Lett. , 31(14): L146031-L146034. doi: 10.1029/2004GL020278 Vanderbilt, D., 1990. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B, 41(11): 7892-7895. doi: 10.1103/PhysRevB.41.7892 Vidale, J.E., Hedlin, M.A.H., 1998. Evidence for Partial Melt at the Core-Mantle Boundary North of Tonga from the Strong Scattering of Seismic Waves. Nature, 391: 682-684. doi: 10.1038/35601 Wen, L., Helmberger, D.V., 1998. Ultra-low Velocity Zones Near the Core-Mantle Boundary from Broadband PKP Precursors. Science, 279(5357): 1701-1703. doi: 10.1126/science.279.5357.1701 Wookey, J., Stackhouse, S., Kendall, J.M., et al., 2005. Efficacy of the Post-Perovskite Phase as an Explanation for Lowermost-mantle Seismic Properties. Nature, 438(7070): 1004-1007. doi: 10.1038/nature04345 Yang, F.Q., Liu, B., Ni, S.D., et al., 2008. Shear Velocity Anisotropy of the Lowermost Mantle Beneath the Siberia. Acta Seismological Sinica, 30(2): 209-213 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DZXB200802011.htm Zhang, F.W., Oganov, A.R., 2006. Valence State and Spin Transitions of Iron in Earth's Mantle Silicates. Earth Planet. Sci. Lett. , 249(3-4): 436-443. doi: 10.1016/j.epsl.2006.07.023 Zhang, Y., Shu, L.S., 2010. On Research Achievements in Earth's D" Layer in Core-Mantle Boundary: An Important Breakthrough in 21st Experimental Petrology. Journal of Geology, 34(2): 113-116 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTotal-JSDZ201002004.htm Zhang, Z.J., 2002. A Review of the Seismic Anisotropy and Its Applications. Progress in Geophysics, 17(2): 281-293 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQWJ200202013.htm Zhao, D.P., 2001. Seismic Structure and Origin of Hotspots and Mantle Plumes. Earth Planet. Sci. Lett. , 192(3): 251-265. doi: 10.1016/S0012-821X(01)00465-4 Zhu, J.S., 2000. Structure of Lower Mantle and Core-Mantle Boundary Region and Its Grodynamics. Advances in Earth Sciences, 15(2): 139-142 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DXJZ200002002.htm 侯渭, 谢鸿森, 周文戈, 2005. 地幔底层及其在全球物质演化中的意义. 地学前缘, 12(1): 37-41. doi: 10.3321/j.issn:1005-2321.2005.01.006 唐群署, 李丽红, 2006. 核幔边界D"区的地震学研究进展. 地学前缘, 13(2): 213-223. doi: 10.3321/j.issn:1005-2321.2006.02.019 杨凤琴, 刘斌, 倪四道, 等, 2008. 西伯利亚下地幔底部的剪切波各向异性. 地震学报, 30(2): 209-213. doi: 10.3321/j.issn:0253-3782.2008.02.010 张苑, 舒良树, 2010.21世纪实验岩石学的重大突破——核幔边界D"层研究. 地质学刊, 34(2): 113-116. doi: 10.3969/j.issn.1674-3636.2010.02.113 张中杰, 2002. 地震各向异性研究进展, 地球物理学进展. 17(2): 281-293. doi: 10.3969/j.issn.1004-2903.2002.02.014 朱介寿, 2000. 下地幔及核幔边界结构及地球动力学. 地球科学进展, 15(2): 139-142. doi: 10.3321/j.issn:1001-8166.2000.02.003 -
下载:
点击查看大图
计量
- 文章访问数: 4840
- HTML全文浏览量: 632
- PDF下载量: 1188
- 被引次数: 0
