Step-Like Displacement Prediction of Landslide Based on Time Series Decomposition and Multivariate Chaotic Model
-
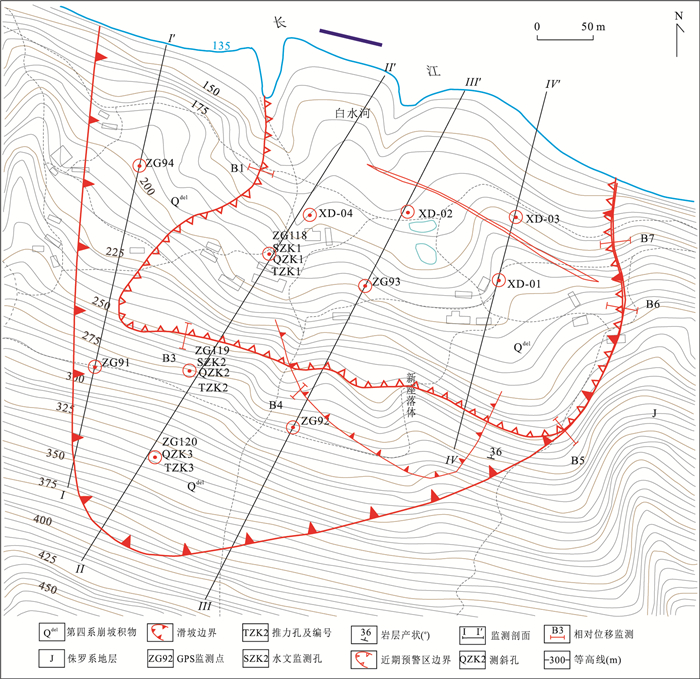
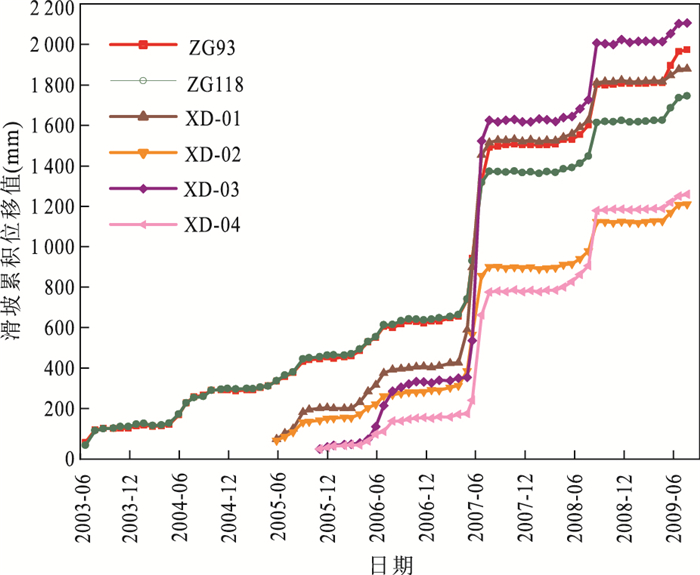
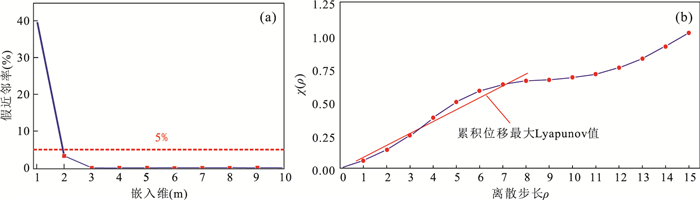
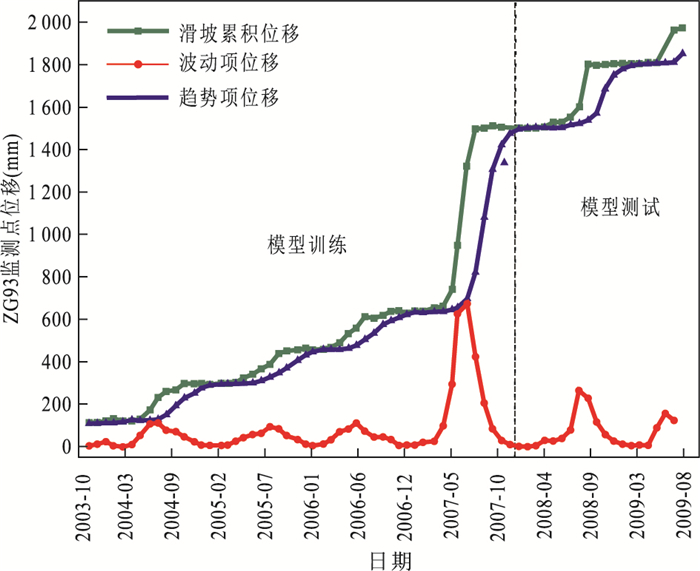
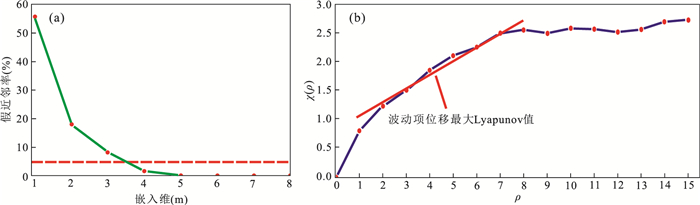
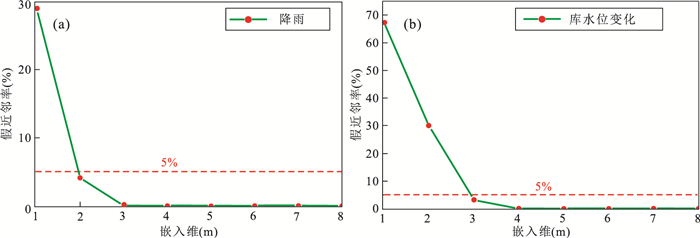
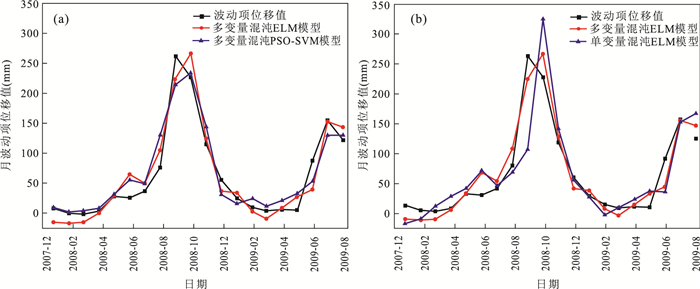
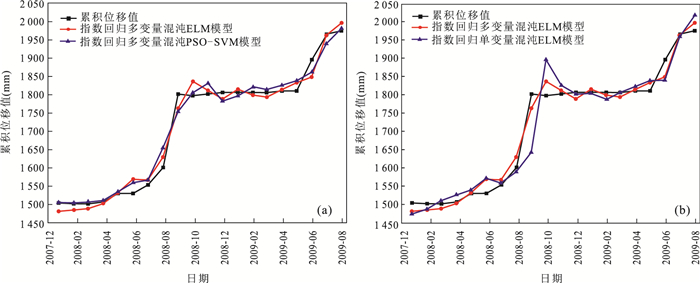
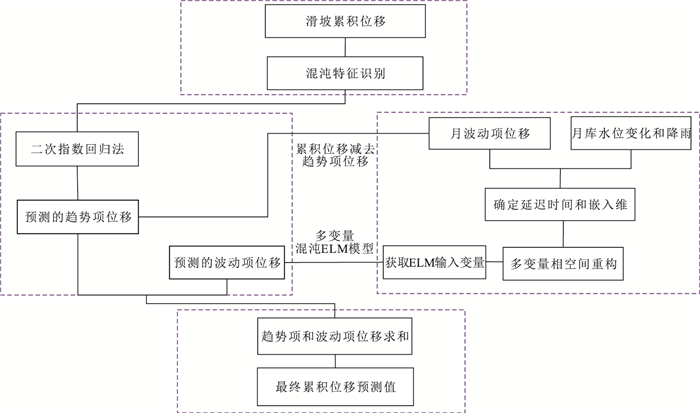
摘要: 三峡库区某些库岸滑坡在强降雨、库水位涨落等诱发因素影响下，其位移时间序列表现出阶跃式变化特征且可能存在混沌特性.但目前常用于滑坡位移预测的混沌模型，均建立在单变量混沌理论的基础之上.且已有的考虑了诱发因素的常规多变量模型，大都采用经验性的方法来选取输入变量；常规多变量模型对滑坡位移序列的非线性特征，及其与诱发因素间的动态响应关系缺乏数学理论上的深入分析.因此，提出一种基于指数平滑法、多变量混沌模型和极限学习机（extreme learing machine，ELM）的滑坡位移组合预测模型.指数平滑多变量混沌ELM模型首先对滑坡累积位移序列的混沌特性进行识别；然后用指数平滑法对累积位移进行预测，得到趋势项位移，并用累积位移减去趋势项位移得到剩余的波动项位移；之后对波动项位移及降雨量、库水位变化量这3个因子进行多变量相空间重构，并用ELM模型对多变量重构后的波动项位移进行预测；最后将预测得到的趋势项和波动项位移值相加，得到最终的累积位移预测值.以三峡库区白水河滑坡ZG93监测点的累积位移作为实例进行分析，并将模型与指数平滑多变量混沌粒子群-支持向量机（PSO-SVM）模型、指数平滑单变量混沌ELM模型作对比.结果表明滑坡位移序列存在混沌特性，模型能有效预测滑坡位移，其预测效果优于对比模型.且本文模型从混沌理论的角度将波动项位移与降雨量、库水位变化量的动态响应关系进行综合分析，更能反映滑坡位移系统演化的物理本质.Abstract: The GPS monitoring cumulative displacement on reservoir landslides in the Three Gorges Reservoir area shows step-like characteristics and is a probable chaotic time series under the influences of the seasonal rainfall and reservoir water level fluctuation. Traditionally, the uni-variable chaotic model is commonly used to predict the landslide displacement; and all existing multivariable models select the input variables empirically without theoretical exploration of the nonlinear dynamic evolution process of landslide displacement and its inducing factors. A new combined model based on double exponential smoothing (DES), multivariable chaotic model, extreme learning machine (ELM) is proposed in this study. First, the chaos characteristic of landslide displacement is identified by the combined DES and multivariable chaotic ELM. Second, the DES method is used to predict the cumulative displacement. The predictive results are the trend displacement, and the periodic displacement is obtained by reducing the trend displacement from the cumulative displacement. Third, the multivariate phase space reconstruction method of chaotic theory is used to explore the dynamic relationship between the periodic displacement and its inducing factors, and the ELM model is established to predict the periodic displacement. Finally, the total forecast cumulative displacement is obtained by adding the predictive trend and periodic displacement. The GPS monitoring cumulative displacement on the Baishuihe landslide is used as case study. In addition, the proposed model is compared with the combined DES and multivariable chaotic particle swarm optimized support vector machine model, the combined DES and uni-variable chaotic ELM model. The results show that the prediction accuracy of the proposed model is higher than that of other models. The proposed model explores the nonlinear characteristic of landslide displacement and its dynamic relationship with inducing factors. The model also reflects the physical meaning of the nonlinear evolution of the landslide displacement.
-
图 1 指数平滑多变量混沌ELM模型流程
Fig. 1. Flow chat of the coupling DES and multivariable chaotic ELM model
图 2 白水河滑坡平面图和监测点布置图
Fig. 2. Topographical map of the Baishuihe landslide, with location of monitoring points
图 4 ZG93监测点累积位移最佳嵌入维(a)和最大Lyapunov指数(b)
Fig. 4. The optimal embedding dimension calculation result (a) and largest Lyapunov exponential value (b) of cumulative displacement of ZG93
图 5 二次指数平滑法提取滑坡趋势项和波动项位移
Fig. 5. Time series decomposition of cumulative displacement of ZG93 using DES method
图 6 滑坡月波动项位移与月降雨量、月平均库水位相关性曲线
Fig. 6. The correlation curve of periodic displacement and rainfall, reservoir water level of ZG93 point
图 7 波动项位移最佳嵌入维(a)和最大Lyapunov指数值(b)
Fig. 7. The optimal embedding dimension (a) and largest Lyapunov exponential value (b) of periodic displacement
图 8 月降雨量(a)和月库水位变化量(b)的嵌入维
Fig. 8. Optimal embedding dimensions of monthly rainfall (a) and monthly water level change (b)
图 9 不同模型的月波动项位移预测值对比
Fig. 9. Comparison between predicted and measured periodic displacement by different models
图 10 滑坡最终累积位移预测结果对比
Fig. 10. Comparison of predicted and measured cumulative displacement
表 1 波动项位移预测模型精度对比
Table 1. Prediction performance comparison of periodic displacement by different models
Models RMSE(mm) R2 多变量混沌ELM 23.71 0.908 单变量混沌ELM 47.67 0.661 多变量混沌PSO-SVM 24.86 0.898 
下载: 导出CSV
-
Basheer, I.A., Hajmeer, M., 2000.Artificial Neural Networks:Fundamentals, Computing, Design, and Application.Journal of Microbiological Methods, 43(1):3-31.https://doi.org/10.1016/s0167-7012(00)00201-3 doi: 10.1016/S0167-7012(00)00201-3 Cai, Z.L., Xu, W.Y., Meng, Y.D., et al., 2015.Prediction of Landslide Displacement Based on GA-LSSVM with Multiple Factors.Bulletin of Engineering Geology and the Environment, 75(2):637-646. https://doi.org/10.13039/501100001809 Chen, D.Y., Han, W.T., 2013.Prediction of Multivariate Chaotic Time Series via Radial Basis Function Neural Network.Complexity, 18(4):55-66.https://doi.org/10.1002/cplx.21441 doi: 10.1002/cplx.v18.4 Fan, X.Y., 2011.Landslide Displacement Multifractal and Its Application to Prediction of Evolvement Trend.Rock and Soil Mechanics, 32(6):1831-1837(in Chinese with English abstract). https://doi.org/10.3969/j.issn.1000-7598.2011.06.038 Gao, W., Feng, X.T., 2004.Study on Displacement Predication of Landslide Based on Grey System and Evolutionary Neural Network.Rock and Soil Mechanics, 25(4):514-517. Garcia, S.P., Almeida, J.S., 2005.Multivariate Phase Space Reconstruction by Nearest Neighbor Embedding with Different Time Delays.Physical Review E, 72(2):027205.https://doi.org/10.1103/physreve.72.027205 doi: 10.1103/PhysRevE.72.027205 Hegger, R., Kantz, H., 1999.Improved False Nearest Neighbor Method to Detect Determinism in Time Series Data.Physical Review E, 60(4):4970-4973.https://doi.org/10.1103/physreve.60.4970 doi: 10.1103/PhysRevE.60.4970 Huang, F.M., Yin, K.L., Zhang, G.R., et al., 2015.Prediction of Groundwater Level in Landslide Using Multivariable PSO-SVM Model.Journal of Zhejiang University (Engineering Science), 49(6):1193-1200(in Chinese with English abstract). http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zjdxxb-gx201506031 Huang, F.M., Huang, J.S., Jiang, S.H., et al., 2017a.Landslide Displacement Prediction Based on Multivariate Chaotic Model and Extreme Learning Machine.Engineering Geology, 218:173-186. https://doi.org/10.1016/j.enggeo.2017.01.016 Huang, F.M., Huang, J.S., Jiang, S.H., et al., 2017b.Prediction of Groundwater Levels Using Evidence of Chaos and Support Vector Machine.Journal of Hydroinformatics, 19(4):586-606. https://doi.org/10.2166/hydro.2017.102 Huang, F.M., Luo, X.Y., Liu, W.P., 2017c.Stability Analysis of Hydrodynamic Pressure Landslides with Different Permeability Coefficients Affected by Reservoir Water Level Fluctuations and Rainstorms.Water, 9(7):450.https://doi.org/10.13039/501100004763 doi: 10.3390/w9070450 Huang, F.M., Yin, K.L., Huang, J.S., et al., 2017d.Landslide Susceptibility Mapping Based on Self-Organizing-Map Network and Extreme Learning Machine.Engineering Geology, 223:11-22.https://doi.org/10.13039/501100001809 doi: 10.1016/j.enggeo.2017.04.013 Huang, F.M., Tian, Y.G., 2014.WA-VOLTERRA Coupling Model Based on Chaos Theory for Monthly Precipitation Forecasting.Earth Science, 39(3):368-374 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQKX201403014.htm Huang, F.M., Yin, K.L., Zhang, G.R., et al., 2016.Landslide Displacement Prediction Using Discrete Wavelet Transform and Extreme Learning Machine Based on Chaos Theory.Environmental Earth Sciences, 75(20):1376.https://doi.org/10.13039/501100004543 doi: 10.1007/s12665-016-6133-0 Huang, G.B., Zhu, Q.Y., Siew, C.K., 2006.Extreme Learning Machine:Theory and Applications.Neurocomputing, 70(1/2/3):489-501. https://doi.org/10.1016/j.neucom.2005.12.126 Lei, S.L., Sun, C.X., Zhou, Q., et al., 2006.The Research of Local Linear Model of Short-Term Electrical Load on Multivariate Time Series.Proceedings of the CSEE, 26(2):25-29(in Chinese with English abstract). Li, A.J., Khoo, S., Lyamin, A.V., et al., 2016.Rock Slope Stability Analyses Using Extreme Learning Neural Network and Terminal Steepest Descent Algorithm.Automation in Construction, 65:42-50. https://doi.org/10.1016/j.autcon.2016.02.004 Lian, C., Zeng, Z.G., Yao, W., et al., 2013.Ensemble of Extreme Learning Machine for Landslide Displacement Prediction Based on Time Series Analysis.Neural Computing and Applications, 24(1):99-107. https://doi.org/10.1007/s00521-013-1446-3 Lu, J.Q., Xu, F., 2011.Research on Prediction Model of Landslide Based on Exponential Smoothing Method and Regression Analysis.Journal of Wuhan University of Technology, 33(10):88-91(in Chinese with English abstract). Nakamura, T., Tanizawa, T., Small, M., 2016.Constructing Networks from a Dynamical System Perspective for Multivariate Nonlinear Time Series.Physical Review E, 93(3):032323.https://doi.org/10.13039/501100001691 doi: 10.1103/PhysRevE.93.032323 Pijn, J.P., van Neerven, J., Noest, A., et al., 1991.Chaos or Noise in EEG Signals; Dependence on State and Brain Site.Electroencephalography and Clinical Neurophysiology, 79(5):371-381.https://doi.org/10.1016/0013-4694(91)90202-f doi: 10.1016/0013-4694(91)90202-F Qin, S.Q., Jiao, J.J., Wang, S.J., 2002.A Nonlinear Dynamical Model of Landslide Evolution.Geomorphology, 43(1/2):77-85. https://doi.org/10.1016/s0169-555x(01)00122-2 Rosenstein, M.T., Collins, J.J., De Luca, C.J., 1993.A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets.Physica D:Nonlinear Phenomena, 65(1/2):117-134. https://doi.org/10.1016/0167-2789(93)90009-p Takens, F., 1981.Detecting Strange Attractors in Turbulence.Springer, Germany. Tan, K., Zhang, Q.Q., Cao, Q., et al., 2015.Hyperspectral Retrieval Model of Soil Organic Matter Content Based on Particle Swarm Optimization-Support Vector Machines.Earth Science, 40(8):1339-1345(in Chinese with English abstract). Tang, L.S., Yin, K.L., 2013.A Study of Displacement Prediction of Progressive Landslide Based on the R/S Analysis Method.Hydrogeology & Engineering Geology, 40(3):93-97(in Chinese with English abstract). Wang, X.Y., Han, M., 2012.Multivariate Chaotic Time Series Prediction Based on Extreme Learning Machine.Acta Physica Sinica, 61(8):97-105(in Chinese with English abstract). http://www.oalib.com/paper/1448243 Wapenaar, K., 2004.Retrieving the Elastodynamic Green's Function of an Arbitrary Inhomogeneous Medium by Cross Correlation.Physical Review Letters, 93(25):254301.https://doi.org/10.1103/physrevlett.93.254301 doi: 10.1103/PhysRevLett.93.254301 Wu, Y.P., Zhang, Q.X., Tang, H.M., et al., 2014.Landslide Hazard Warning Based on Effective Rainfall Intensity.Earth Science, 39(7):889-895(in Chinese with English abstract). Xiong, S., He, Y.G., Ji, F., et al., 2013.Application of Exponential Smoothing to Prediction of Deep Displacement in Foundation Pit.Mining and Metallurgical Engineering, 33(2):5-7(in Chinese with English abstract). https://doi.org/10.3969/j.issn.0253-6099.2013.02.002 Xu, Q., Tang, M.G., Xu, K.X., et al., 2008.Research on Space-Time Evolution Laws and Early Warning-Prediction of Landslides.Chinese Journal of Rock Mechanics and Engineering, 27(6):1104-1112(in Chinese with English abstract). Yang, Y.G., Chen, Y.H., 2009.Chaotic Characteristic and Prediction for Water Inrush in Mine.Earth Science, 34(2):258-262(in Chinese with English abstract). Zhang, J., Yin, K.L., Wang, J.J., et al., 2015.Displacement Prediction of Baishuihe Landslide Based on Time Series and PSO-SVR Model.Chinese Journal of Rock Mechanics and Engineering, 34(2):382-391 (in Chinese with English abstract). Zhao, M., Fan, Y.H., Sun, H., 2008.Chaos Local Forecasting of Electric Propulsion Ship Power Load on Multivariate Time Series.Journal of System Simulation, 20(11):2797-2799, 2805(in Chinese with English abstract). Zhou, C.Y., Chen, H., Zhu, F.X., 2008.Multivariable Chaotic Discrimination for Slope Evaluation According to Their Nonlinear Displacement-Time Sequence.Earth Science, 33(3):393-398(in Chinese with English abstract). Zhou, C.Y., Yin, K., Huang, F., 2015.Displacement Prediction of Step-Like Landslide Based on the Response of Inducing Factors and Support Vector Machine.Chinese Journal of Rock Mechanics and Engineering, 2:4132-4139. Zhou, C.Y., Zhang, L., Huang, X.Y., 2005.Classification of Rocks Surrounding Tunnel Based on Improved BP Network Algorithm.Earth Science, 30(4):480-486(in Chinese with English abstract). 樊晓一, 2011.滑坡位移多重分形特征与滑坡演化预测.岩土力学, 32(6):1831-1837. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ytlx201106038 黄发明, 田玉刚, 2014.混沌序列WA-VOLTERRA耦合模型在月降水量预测中的应用.地球科学, 39(3):368-374. http://www.earth-science.net/WebPage/Article.aspx?id=2845 黄发明, 殷坤龙, 张桂荣, 等, 2015.多变量PSO-SVM模型预测滑坡地下水位.浙江大学学报(工学版), 49(6):1193-1200. http://www.cqvip.com/QK/90076X/201506/665320182.html 雷绍兰, 孙才新, 周湶, 等, 2006.电力短期负荷的多变量时间序列线性回归预测方法研究.中国电机工程学报, 26(2):25-29. http://jz.docin.com/p-511744598.html 卢继强, 徐峰, 2011.基于指数平滑法和回归分析的滑坡预报模型研究.武汉理工大学学报, 33(10):88-91. doi: 10.3963/j.issn.1671-4431.2011.10.020 谭琨, 张倩倩, 曹茜, 等, 2015.基于粒子群优化支持向量机的矿区土壤有机质含量高光谱反演.地球科学, 40(8):1339-1345. http://www.earth-science.net/WebPage/Article.aspx?id=3136 汤罗圣, 殷坤龙, 2013.基于R/S分析方法的渐进式滑坡位移预测研究.水文地质工程地质, 40(3):93-97. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_swdzgcdz201303018 王新迎, 韩敏, 2012.基于极端学习机的多变量混沌时间序列预测.物理学报, 61(8):97-105. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_wlxb201208014 吴益平, 张秋霞, 唐辉明, 等, 2014.基于有效降雨强度的滑坡灾害危险性预警.地球科学, 39(7):889-895. http://www.earth-science.net/WebPage/Article.aspx?id=2892 熊莎, 贺跃光, 姬方, 等, 2013.指数平滑法在基坑深层位移预测中的应用.矿冶工程, 33(2):5-7. doi: 10.3969/j.issn.0253-6099.2013.02.002 许强, 汤明高, 徐开祥, 等, 2008.滑坡时空演化规律及预警预报研究.岩石力学与工程学报, 27(6):1104-1112. https://www.wenkuxiazai.com/doc/ddbc681ff46527d3240ce0be.html 杨永国, 陈玉华, 2009.矿井涌水量混沌特征与预测.地球科学, 34(2):258-262. http://www.earth-science.net/WebPage/Article.aspx?id=1822 张俊, 殷坤龙, 王佳佳, 等, 2015.基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究.岩石力学与工程学报, 34(2):382-391. http://www.cnki.com.cn/Article/CJFDTotal-YSLX201502019.htm 赵敏, Fan, Y.H., 孙辉, 2008.电力推进船舶电力负荷的多变量混沌局部预测.系统仿真学报, 20(11):2797-2799, 2805. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xtfzxb200811003 周翠英, 陈恒, 朱凤贤, 2008.边坡演化的非线性时间序列多元混沌判别.地球科学, 33(3):393-398. http://www.earth-science.net/WebPage/Article.aspx?id=1706 周翠英, 张亮, 黄显艺, 2005.基于改进BP网络算法的隧洞围岩分类.地球科学, 30(4):480-486. http://www.earth-science.net/WebPage/Article.aspx?id=1404 -
点击查看大图
图(10) / 表(1)
计量
- 文章访问数: 4845
- HTML全文浏览量: 1999
- PDF下载量: 46
- 被引次数: 0
