Primary Controlling Factors and Statistical Modeling of Plume Stability for BTEX in Typical Phreatic Aquifers
-
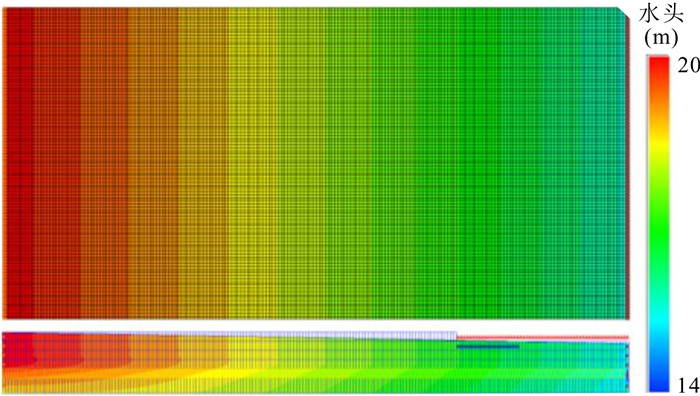
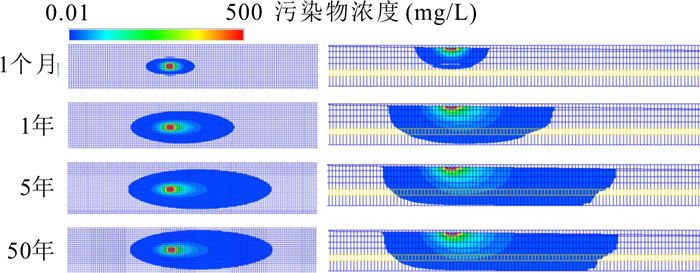
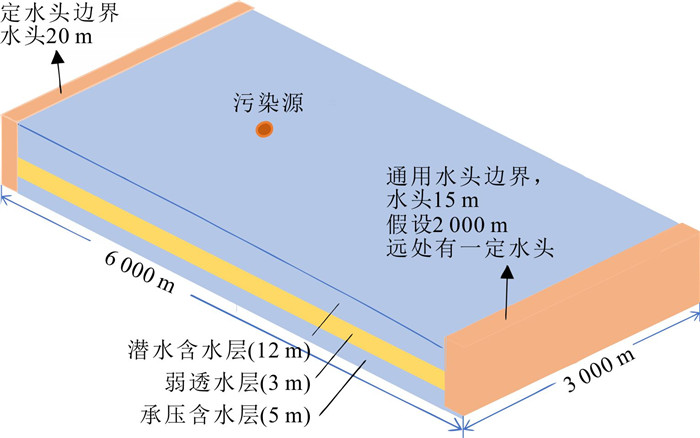
摘要: 场地或区域地下水污染羽能否达到稳定及其稳定性特征直接决定自然衰减修复的可行性.本文构建了从上到下依次为潜水层、弱透水层、承压层的典型含水结构，模拟量化潜水层恒定源地下水污染羽迁移扩散，以污染羽稳定面积、稳定浓度和稳定所需时间为特征因子，充分考虑可能影响污染羽迁移扩散的水文地质和水化学参数.首先通过敏感性分析筛选出较敏感因子，然后利用正交试验进行主控因子识别，最后采用多元回归模型构建特征因子与主控因子的定量统计关系.结果表明，对污染羽特征因子具有广泛影响的主控因子为降解系数、弥散度、渗流速度和源浓度，特征因子与主控因子之间具有良好的统计关系，根据实际情况可选用不同主控因子数量表征的统计模型对特征因子进行预测，这将为基于自然衰减修复的场地或区域地下水污染优化控制与高效修复提供重要依据.Abstract: Whether the groundwater pollution plume of a contaminated site or a regional area can be stabilized and the stability characteristics of the plume would directly determine the feasibility of the natural attenuation restoration. In this study, a typical aquifer structure with a phreatic aquifer, an impermeable aquifer, and a confined aquifer from top to bottom was constructed to simulate the migration and diffusion of the constant source pollution plume of phreatic water. The stable area, stable concentration and starting stable time of the groundwater pollution plume were taken as characteristic variables. Firstly, the sensitive factors were identified from numerous influence factors through sensitivity analysis method. Secondly, orthogonal experiments were used to identify the main controlling factors. Finally, the multiple regression model was used to construct the quantitative statistical relationship for characteristic variables. The results show that the common primary controlling factors are the degradation coefficient, dispersivity, seepage velocity and the source concentration. Moreover, there are adequate statistical relationships between the characteristic variables and the primary controlling factors. The statistical models characterized by different numbers of factors can be used to predict the characteristic variables. This study would provide an important basis for optimization of the site pollution control and effective remediation which are based on natural attenuation remediation.
-
图 4 污染羽稳定性特征因子随各参数变幅的变化
Fig. 4. Changes of pollution plume stable characteristic factors as the parameter changed
图 6 污染羽稳定面积、稳定浓度、稳定时间的回归模型残差
Fig. 6. Regression model residuals of stable area, stable concentration and stable time of pollution plume
表 1 模型初始参数设置
Table 1. Model initial parameters setting
参数名称 输入值 降水入渗补给强度R（m/d） 0.000 2 有效孔隙度P 0.2 潜水含水层渗透系数Kw（m/d） 50 弱透水层渗透系数Ka（m/d） 0.008 承压水含水层渗透系数（m/d） 50 潜水含水层厚度Mw（m） 12 弱透水层厚度Ma（m） 3 承压含水层厚度（m） 5 潜水与承压水水头差ΔHv（m） 1 上游与下游水头差ΔHh（m） 5 降解系数Dg（1/d） 0.005 吸附系数Kd（m3/kg） 0.000 1 污染源浓度C0（mg/L） 500 弥散度D（m） 60 污染源面积A（m2） 900 污染源厚度占潜水含水层比值 0.25 注：表中污染物迁移相关系数参考BIOSCREEN: Natural Attenuation Decision Support System. User's Manual ( Newell et al., 1996 ).
下载: 导出CSV
表 2 各参数变化情况下污染羽稳定性特征因子变化率
Table 2. The amplitude of pollution plume stable characteristic factors under different amplitudes of parameters
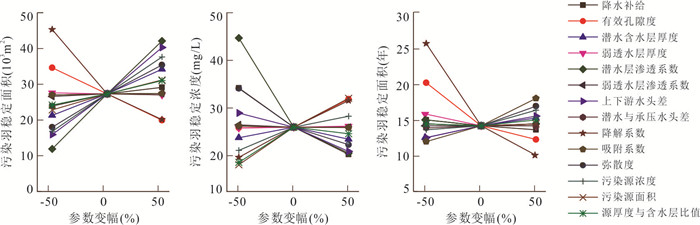
稳定面积变化率 稳定浓度变化率 稳定时间变化率 参数变幅 增大50% 减小50% 平均变化率 增大50% 减小50% 平均变化率 增大50% 减小50% 平均变化率 降水入渗补给强度 0.066 0.125 0.095 0.220 0.316 0.268 0.038 0.058 0.048 有效孔隙度 0.271 0.267 0.269 0.226 0.006 0.116 0.135 0.423 0.279 潜水含水
层厚度0.253 0.220 0.236 0.097 0.084 0.091 0.077 0.115 0.096 弱透水
层厚度0.011 0.011 0.011 0.009 0.008 0.008 0.000 0.115 0.058 潜水层渗
透系数0.542 0.564 0.553 0.210 0.720 0.465 0.019 0.058 0.038 弱透水层渗透系数 0.004 0.026 0.015 0.002 0.018 0.010 0.019 0.000 0.010 上下游
水头差0.476 0.418 0.447 0.195 0.114 0.154 0.096 0.115 0.106 潜水与承压水头差 0.004 0.011 0.007 0.001 0.008 0.004 0.000 0.019 0.010 降解系数 0.264 0.659 0.462 0.215 0.243 0.229 0.288 0.808 0.548 吸附系数 0.004 0.011 0.007 0.003 0.010 0.007 0.269 0.154 0.212 弥散度 0.297 0.341 0.319 0.141 0.313 0.227 0.192 0.019 0.106 污染源浓度 0.377 0.385 0.381 0.089 0.188 0.138 0.154 0.038 0.096 污染源面积 0.143 0.165 0.154 0.234 0.303 0.269 0.019 0.019 0.019 源厚度与含水层比值 0.136 0.114 0.125 0.053 0.284 0.169 0.058 0.019 0.038 注：此表中变化率均为绝对值.
下载: 导出CSV
表 3 因素水平表
Table 3. Design of parameter levels
水平 降解系数（1/d） 吸附系数
（m3/kg）弥散度
（m）源浓度（mg/L） 源面积
（400m2）源厚度占比
(%)渗流速度（m/d） 有效
孔隙度1 0.002 0.000 01 10 10 1 0.2 0.005 0.10 2 0.005 0.000 05 30 50 2 0.4 0.020 0.15 3 0.01 0.000 10 60 100 3 0.6 0.050 0.20 4 0.05 0.000 50 100 200 4 0.8 0.100 0.30 5 0.1 0.001 0 200 500 5 1.0 0.200 0.40
下载: 导出CSV
表 4 正交设计表及试验结果
Table 4. Orthogonal experimental design table and experimental results
序号 降解
系数吸附
系数弥散度 源浓度 源面积 源厚度占比 渗流
速度有效
孔隙度稳定面积
（103m2）稳定浓度
（mg/L）稳定时间（a） 1 1 1 1 1 1 1 1 1 18.0 0.18 2.9 2 1 2 2 2 2 2 2 2 61.6 1.18 8.6 3 1 3 3 3 3 3 3 3 118.8 3.09 16.2 4 1 4 4 4 4 4 4 4 517.2 3.79 33.2 5 1 5 5 5 5 5 5 5 2 006.0 8.10 68.2 6 2 1 2 3 4 5 1 2 60.8 9.38 3.6 7 2 2 3 4 5 1 2 3 61.6 2.45 4.8 8 2 3 4 5 1 2 3 4 61.6 4.26 5.9 9 2 4 5 1 2 3 4 5 125.2 0.42 16.6 10 2 5 1 2 3 4 5 1 368.0 1.44 9.1 11 3 1 3 5 2 4 4 1 72.0 15.2 0.6 12 3 2 4 1 3 5 5 2 65.2 0.66 0.6 13 3 3 5 2 4 1 1 3 22.4 0.51 1.2 14 3 4 1 3 5 2 2 4 4.4 0.90 1.2 15 3 5 2 4 1 3 3 5 4.8 11.21 1.7 16 4 1 4 2 5 3 5 3 297.6 1.70 2.4 17 4 2 5 3 1 4 1 4 57.6 2.43 2.6 18 4 3 1 4 2 5 2 5 8.0 23.79 2.7 19 4 4 2 5 3 1 3 1 41.6 3.03 12.4 20 4 5 3 1 4 2 4 2 68.0 0.40 8.5 21 5 1 5 4 3 2 4 3 48.0 3.76 0.4 22 5 2 1 5 4 3 5 4 16.0 48.35 0.5 23 5 3 2 1 5 4 1 5 6.8 3.05 0.3 24 5 4 3 2 1 5 2 1 7.2 3.58 1.0 25 5 5 4 3 2 1 3 2 6.4 0.25 1.2 26 1 1 1 4 5 4 3 2 73.2 12.22 9.5 27 1 2 2 5 1 5 4 3 359.2 5.41 15.6 28 1 3 3 1 2 1 5 4 248.0 0.46 9.3 29 1 4 4 2 3 2 1 5 90.8 1.24 20.3 30 1 5 5 3 4 3 2 1 703.2 1.34 114.5 31 2 1 2 1 3 3 2 4 14.4 1.26 2.1 32 2 2 3 2 4 4 3 5 30.4 4.17 3.8 33 2 3 4 3 5 5 4 1 565.6 2.60 15.9 34 2 4 5 4 1 1 5 2 1 132.0 0.98 32.6 35 2 5 1 5 2 2 1 3 26.4 6.80 15.3 36 3 1 3 3 1 2 5 5 38.0 1.43 0.7 37 3 2 4 4 2 3 1 1 46.4 8.40 1.2 38 3 3 5 5 3 4 2 2 57.2 24.96 1.8 39 3 4 1 1 4 5 3 3 10.4 1.90 3.6 40 3 5 2 2 5 1 4 4 19.2 0.54 3.9 41 4 1 4 5 4 1 2 5 31.2 3.25 2.5 42 4 2 5 1 5 2 3 1 78.0 0.47 2.5 43 4 3 1 2 1 3 4 2 29.2 1.85 2.6 44 4 4 2 3 2 4 5 3 161.2 2.87 9.0 45 4 5 3 4 3 5 1 4 38.0 10.95 10.0 46 5 1 5 2 2 5 3 4 10.4 5.05 0.3 47 5 2 1 3 3 1 4 5 2.0 0.44 0.2 48 5 3 2 4 4 2 5 1 46.4 4.26 0.7 49 5 4 3 5 5 3 1 2 20.8 55.48 1.7 50 5 5 4 1 1 4 2 3 4.8 1.02 0.7
下载: 导出CSV
表 5 正交试验极差分析结果
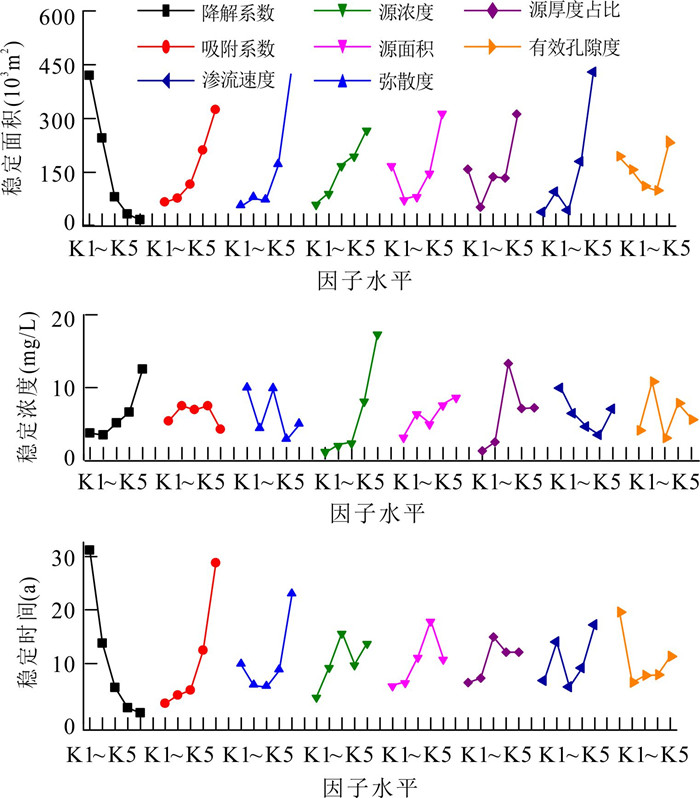
Table 5. Range analysis results of the orthogonal experiment
降解系数 吸附系数 弥散度 源浓度 源面积 源厚度占比 渗流速度 有效孔隙度 稳
定
面
积K1 1 049.00 165.90 138.90 159.70 428.10 395.60 97.00 486.60 K2 611.50 194.50 194.00 234.20 191.40 130.80 238.40 393.60 K3 202.60 291.00 175.70 429.50 211.00 344.10 108.90 277.60 K4 85.00 527.70 421.70 493.90 376.50 337.10 451.40 246.70 K5 42.20 811.20 1 060.00 673.00 783.30 782.70 1 094.60 585.80 R 1 006.80 645.30 921.10 513.30 591.90 651.90 997.60 339.10 主次： 降解系数 > 渗流速度 > 弥散度 > 源厚度占比 > 吸附系数 > 源面积 > 源浓度 > 有效孔隙度 稳
定
浓
度K1 3.701 5.343 9.787 0.982 3.235 1.209 9.842 4.050 K2 3.376 7.396 4.219 2.126 6.442 2.470 6.373 10.736 K3 5.074 6.883 9.721 2.473 5.083 13.310 4.565 2.951 K4 6.571 7.419 2.717 8.181 7.735 7.115 3.441 7.799 K5 12.524 4.205 4.802 17.484 8.751 7.142 7.025 5.710 R 9.15 3.21 7.07 16.50 5.52 12.10 6.40 7.79 主次： 源浓度 > 源厚度占比 > 降解系数 > 有效孔隙度 > 弥散度 > 渗流速度 > 源面积 > 吸附系数 稳
定
时
间K1 31.15 2.50 9.76 3.76 5.93 6.37 6.78 19.53 K2 13.77 3.99 5.79 9.39 6.48 7.26 13.99 6.37 K3 5.47 4.93 5.56 15.81 11.31 14.95 5.56 7.69 K4 1.62 12.46 8.69 9.88 18.08 12.06 9.15 7.80 K5 0.70 28.83 22.91 13.87 10.91 12.07 17.23 11.32 R 30.45 26.33 17.35 12.05 12.15 8.58 11.67 13.16 主次： 降解系数 > 吸附系数 > 弥散度 > 有效孔隙度 > 源面积 > 源浓度 > 渗流速度 > 源厚度占比
下载: 导出CSV
表 6 影响因子方差分析
Table 6. Variance analysis of influencing factors
稳定面积 稳定浓度 稳定时间 参数 均方 F值 显著性 均方 F值 显著性 均方 F值 显著性 降解系数 1 830 318 5.93 0.004** 139 2.15 0.119 1 593 10.00 0.000** 吸附系数 735 720 2.38 0.092 20 0.31 0.866 1 193 7.49 0.001** 弥散度 1 492 429 4.84 0.009** 108 1.67 0.203 511 3.21 0.039* 源浓度 423 578 1.37 0.285 472 7.29 0.001** 216 1.36 0.289 源面积 568 692 1.84 0.167 47 0.73 0.583 238 1.50 0.248 源厚度占比 565 024 1.83 0.169 228 3.51 0.029* 131 0.82 0.530 渗流速度 1 719 388 5.57 0.005** 61 0.94 0.467 244 1.53 0.238 孔隙度 201 315 0.65 0.633 96 1.49 0.250 286 1.80 0.176 注：**表示P小于0.01，表明参数变化对结果有非常显著的影响，*表示P大于0.01且小于0.05，表明参数变化对结果有显著影响.
下载: 导出CSV
表 7 多元回归分析结果
Table 7. Results of multiple regression analysis
因变量 模型 稳定
面积
lnS1
R2=0.781参数 (常量) lnDg lnv lnD lnP 系数 ‒0.281 ‒0.696 0.599 0.437 ‒0.71 显著性 0.667 0.000 0.000 0.000 0.001 2
R2= 0.81参数 (常量) lnDg lnv lnD lnP lnC0 系数 ‒1.17 ‒0.696 0.599 0.437 ‒0.71 0.199 显著性 0.094 0.000 0.000 0.000 0.001 0.08 3
R2= 0.825参数 (常量) lnDg lnv lnD lnP lnC0 lnA 系数 ‒1.17 ‒0.696 0.599 0.437 ‒0.71 0.199 0.352 显著性 0.163 0.000 0.000 0.000 0.000 0.006 0.032 4
R2= 0.839参数 (常量) lnDg lnv lnD lnP lnC0 lnA lnr 系数 ‒1.17 ‒0.696 0.599 0.437 ‒0.71 0.199 0.352 0.333 显著性 0.023 0.000 0.000 0.000 0.000 0.004 0.026 0.034 稳定
浓度
lnC1
R2=0.756参数 (常量) lnC0 lnr 系数 ‒1.353 0.693 1.230 显著性 0.000 0.000 0.000 2
R2= 0.772参数 (常量) lnC0 lnr lnv 系数 ‒1.822 0.693 1.230 ‒0.146 显著性 0.000 0.000 0.000 0.043 稳定
时间
lnT1
R2= 0.899参数 (常量) lnDg lnKd 系数 1.066 ‒0.848 0.384 显著性 0.014 0.000 0.000 2
R2= 0.917参数 (常量) lnDg lnKd lnC0 系数 0.391 ‒0.848 0.384 0.151 显著性 0.366 0.000 0.000 0.002 3
R2= 0.933参数 (常量) lnDg lnKd lnC0 lnD 系数 ‒0.333 ‒0.848 0.384 0.151 0.184 显著性 0.448 0.000 0.000 0.001 0.001 4
R2= 0.938参数 (常量) lnDg lnKd lnC0 lnD lnv 系数 ‒0.685 ‒0.848 0.384 0.151 0.184 0.222 显著性 0.136 0.000 0.000 0.000 0.001 0.04 5
R2= 0.943参数 (常量) lnDg lnKd lnC0 lnD lnv lnA 系数 1.127 ‒0.848 0.384 0.151 0.184 0.222 0.189 显著性 0.023 0.000 0.000 0.000 0.000 0.033 0.036
下载: 导出CSV
-
Bou⁃Zeid, E., El⁃Fadel, M., 2004. Parametric Sensitivity Analysis of Leachate Transport Simulations at Landfills. Waste Management, 24(7): 681-689. https://doi.org/10.1016/j.wasman.2004.03.004 Gedeon, M., Mallants, D., 2012. Sensitivity Analysis of a Combined Groundwater Flow and Solute Transport Model Using Local–Grid Refinement: A Case Study. Mathematical Geosciences, 44(7): 881-899. https://doi.org/10.1007/s11004–012–9416–3 Hao, J., Jia, Y. W., Zhang, Y. X., et al., 2015. Application of Orthogonal Experiment on Parameter Sensitivity Analysis of Groundwater Simulation. Yellow River, 37(9): 66-68 (in Chinese with English abstract). doi: 10.3969/j.issn.1000-1379.2015.09.018 Huang, F. M., Ye, Z., Yao, C., et al., 2020. Uncertainties of Landslide Susceptibility Prediction: Different Attribute Interval Divisions of Environmental Factors and Different Data⁃Based Models. Earth Science, 45(12): 4535-4549 (in Chinese with English abstract). Li, L., 2011. Quantifying TiO2 Abundance of Lunar Soils: Partial Least Squares and Stepwise Multiple Regression Analysis for Determining Causal Effect. Journal of Earth Science, 22(5): 549-565. https://doi.org/10.1007/s12583–011–0206–5 Li, M. Z., Zhai, Y. Z., Zuo, R., et al., 2014. Sensitivity Analysis of Parameters in Numerical Simulation of Solute Transport in Groundwater. South–to–North Water Transfers and Water Science & Technology, 12(3): 133-137 (in Chinese with English abstract). Li, X. N., Chen, W. P., Lü, S. D., 2022. Advancement in Researches on Technical Systems and Modes for Risk Management and Control of Contaminated Sites at Home and Aborad. Acta Pedologica Sinica, 59(1): 38-53 (in Chinese with English abstract). Li, Y. J., Wang, S. J., Zhang, M., et al., 2018. Research Progress of Monitored Natural Attenuation Remediation Technology for Soil and Groundwater Pollution. China Environmental Science, 38(3): 1185-1193 (in Chinese with English abstract). doi: 10.3969/j.issn.1000-6923.2018.03.047 Lide, D. R., 1999. CRC Handbook of Chemistry and Physics. 80th Edition, CRC Press, Boca Raton. Ma, L., Feng, C. C., 2014. Analysis on Sustainable Utilization and Exploitation Potentiality of Shallow Groundwater Resources in Heze Yellow River Flood Plain Areas. Shandong Land and Resources, 30(2): 43-46 (in Chinese with English abstract). Ma, Z. F., An, D., Jiang, Y. H., et al., 2012. Simulation on Contamination Forecast and Control of Groundwater in a Certain Hazardous Waste Landfill. Environmental Science, 33(1): 64-70 (in Chinese with English abstract). Newell, C. J., McLeod, R. K., Gonzales, J. R., 1996. BIOSCREEN: Natural Attenuation Decision Support System. User's Manual Version 1.3. United States Environmental Protection Agency, Office of Research and Development, Washington D. C. . Ni, H., Liu, Y. R., Long, Z. G., 2002. Applications of Orthogonal Design to Sensitivity Analysis of Landslide. Chinese Journal of Rock Mechanics and Engineering, 21(7): 989-992 (in Chinese with English abstract). doi: 10.3321/j.issn:1000-6915.2002.07.010 Shao, B. R., Sun, J. C., Zhu, Y. Q., et al., 2020. Research on Gliding Distance Estimation of Loess Landslide Based on Multiple Regression: A Case Study of Tianshui Region, Gansu Province. Geological Bulletin of China, 39(12): 1993-2003 (in Chinese with English abstract). doi: 10.12097/j.issn.1671-2552.2020.12.013 Shen, X. F., Wan, Y. Y., Wang, L. G., et al., 2021. Multiphase Flow Modeling of Natural Attenuation of Volatile Organic Compounds (VOCs) in a Petroleum Contaminated Site. Earth Science Frontiers, 28(5): 90-103 (in Chinese with English abstract). Su, Z. X., Gao, W. S., Du, F. L., et al., 2020. Numerical Simulation and Parameter Sensitivity Analysis of Pollutant Migration in Stratified Soil. Journal of Geological Hazards and Environment Preservation, 31(4): 53-62 (in Chinese with English abstract). Wang, F., Jiao, Z. H., 2014. Application of Orthogonal Design in Sensitivity Analysis of Factors Influencing Landslide Stability. Resources Environment & Engineering, 28(4): 394-397 (in Chinese with English abstract). doi: 10.3969/j.issn.1671-1211.2014.04.004 Wang, Y. T., Li, J. X., Xue, X. B., et al., 2021. Similarities and Differences of Main Controlling Factors of Natural High Iodine Groundwater between North China Plain and Datong Basin. Earth Science, 46(1): 308-320 (in Chinese with English abstract). Xiao, B., Cui, B. L., Jiang, B. F., et al., 2019. Spatial and Temporal Variations of Rainfall Erosivity in Different Topographic Regions of Shandong Province. Journal of Earth Environment, 10(3): 267-280 (in Chinese with English abstract). Xu, C., Ye, G. B., 2004. Parameter Sensitivity Analysis of Numerical Model by Cross Test Design Technique. Hydrogeology and Engineering Geology, 31(1): 95-97 (in Chinese with English abstract). Yan, Y., Wang, M. Y., Chen, J. P., et al., 2021. Lab Experiments and Numerical Simulations of 1, 2⁃DCA Remediation in Groundwater at Contaminated Sites. Earth and Environment, 49(3): 250-259 (in Chinese with English abstract). Yang, X. F., Wang, M. Y., Wang, L. Y., et al., 2015. Investigation of Key Controlling Factors and Numerical Simulation Uncertainty of the Groundwater Level Companying with Yongding River Ecological Restoration. Journal of University of Chinese Academy of Sciences, 32(2): 192-199 (in Chinese with English abstract). Zhai, Y. Z., Wang, J. S., Su, X. S., 2011. Sensitivity Analysis of Groundwater Numerical Simulation Using Orthogonal Experiment. Geotechnical Investigation & Surveying, 39(1): 46-50 (in Chinese with English abstract). Zhu, C. J., Li, J. X., Xie, X. J., 2021. Carbon and Sulfur Isotopic Features and Its Implications for Iodine Mobilization in Groundwater System at Datong Basin, Northern China. Earth Science, 46(12): 4480-4491 (in Chinese with English abstract). 郝静, 贾仰文, 张永祥, 等, 2015. 应用正交试验法分析地下水流模型参数灵敏度. 人民黄河, 37(9): 66-68. https://www.cnki.com.cn/Article/CJFDTOTAL-RMHH201509021.htm 黄发明, 叶舟, 姚池, 等, 2020. 滑坡易发性预测不确定性: 环境因子不同属性区间划分和不同数据驱动模型的影响. 地球科学, 45(12): 4535-4549. doi: 10.3799/dqkx.2020.247 李木子, 翟远征, 左锐, 等, 2014. 地下水溶质迁移数值模型中的参数敏感性分析. 南水北调与水利科技, 12(3): 133-137. https://www.cnki.com.cn/Article/CJFDTOTAL-NSBD201403029.htm 李笑诺, 陈卫平, 吕斯丹, 2022. 国内外污染场地风险管控技术体系与模式研究进展. 土壤学报, 59(1): 38-53. https://www.cnki.com.cn/Article/CJFDTOTAL-TRXB202201004.htm 李元杰, 王森杰, 张敏, 等, 2018. 土壤和地下水污染的监控自然衰减修复技术研究进展. 中国环境科学, 38(3): 1185-1193. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHJ201803052.htm 马龙, 冯超臣, 2014. 菏泽黄泛平原地区浅层地下水资源可持续开发利用潜力分析. 山东国土资源, 30(2): 43-46. https://www.cnki.com.cn/Article/CJFDTOTAL-SDDI201402012.htm 马志飞, 安达, 姜永海, 等, 2012. 某危险废物填埋场地下水污染预测及控制模拟. 环境科学, 33(1): 64-70. https://www.cnki.com.cn/Article/CJFDTOTAL-HJKZ201201013.htm 倪恒, 刘佑荣, 龙治国, 2002. 正交设计在滑坡敏感性分析中的应用. 岩石力学与工程学报, 21(7): 989-992. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200207011.htm 邵葆蓉, 孙即超, 朱月琴, 等, 2020. 基于多元回归的黄土滑坡滑动距离预测模型探讨——以甘肃天水地区为例. 地质通报, 39(12): 1993-2003. https://www.cnki.com.cn/Article/CJFDTOTAL-ZQYD202012015.htm 沈晓芳, 万玉玉, 王利刚, 等, 2021. 基于多相流数值模拟的某石油污染场地地下水中VOCs自然衰减过程识别及能力评估. 地学前缘, 28(5): 90-103. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY202105013.htm 苏振兴, 高文生, 杜风雷, 等, 2020. 成层土中污染物迁移数值模拟及参数敏感性分析. 地质灾害与环境保护, 31(4): 53-62. https://www.cnki.com.cn/Article/CJFDTOTAL-DZHB202004011.htm 王帆, 焦振华2014. 正交设计法在滑坡稳定性影响因素敏感性分析中的应用. 资源环境与工程, 28(4): 394-397. https://www.cnki.com.cn/Article/CJFDTOTAL-HBDK201404005.htm 王雨婷, 李俊霞, 薛肖斌, 等, 2021. 华北平原与大同盆地原生高碘地下水赋存主控因素的异同. 地球科学, 46(1): 308-320. doi: 10.3799/dqkx.2019.261 肖蓓, 崔步礼, 姜宝福, 等, 2019. 山东省不同地形区降雨侵蚀力时空变化特征. 地球环境学报, 10(3): 267-280. https://www.cnki.com.cn/Article/CJFDTOTAL-DQHJ201903006.htm 徐超, 叶观宝, 2004. 应用正交试验设计进行数值模型参数的敏感性分析. 水文地质工程地质, 31(1): 95-97. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG200401023.htm 闫龑, 王明玉, 陈建平, 等, 2021. 场地地下水1, 2‒二氯乙烷污染的修复实验与数值模拟研究. 地球与环境, 49(3): 250-259. https://www.cnki.com.cn/Article/CJFDTOTAL-DZDQ202103003.htm 杨小芳, 王明玉, 王丽亚, 等, 2015. 永定河生态修复地下水位主控因素与数值模拟预测不确定性. 中国科学院大学学报, 32(2): 192-199. https://www.cnki.com.cn/Article/CJFDTOTAL-ZKYB201502007.htm 翟远征, 王金生, 苏小四, 2011. 正交试验法在地下水数值模拟敏感性分析中的应用. 工程勘察, 39(1): 46-50. https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC201101012.htm 朱沉静, 李俊霞, 谢先军, 2021. 大同盆地地下水中碳硫同位素组成特征及其对碘迁移富集的指示. 地球科学, 46(12): 4480-4491. doi: 10.3799/dqkx.2021.090 -
点击查看大图
图(6) / 表(7)
计量
- 文章访问数: 486
- HTML全文浏览量: 651
- PDF下载量: 25
- 被引次数: 0
