A Review of Retrogressive Thaw Slumps Characteristics, Evolution, and Permafrost Stability Analysis Methods
-
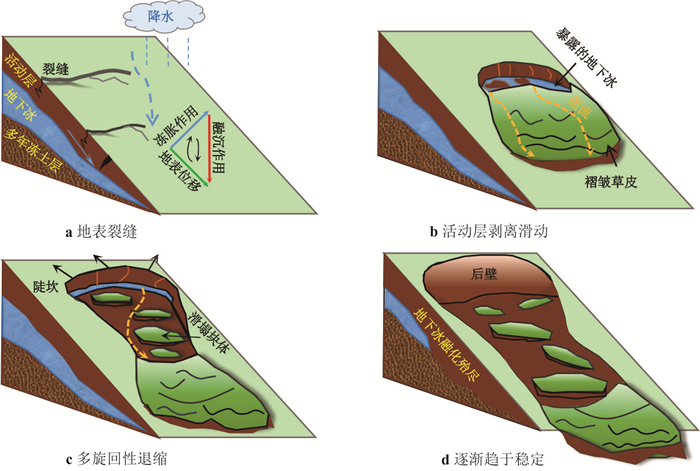
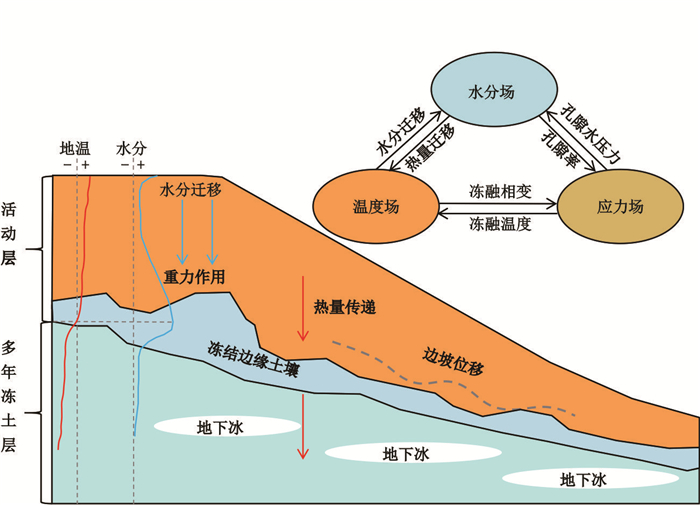
摘要: 在全球气候变暖的背景下,加速退化的多年冻土降低了边坡稳定性,诱发热融滑塌等冻土灾害,严重威胁寒区的工程稳定性和生态环境安全.然而,当前学界对热融滑塌形态特征与演化过程的认知仍不充分,且模型模拟方法体系和适用性缺乏系统综述.因此,结合多年野外考察和文献资料,从热融滑塌的形态特征、演化过程、失稳机理和模拟方法4个方面进行了综述.研究发现:(1)热融滑塌形态特征可以划分为11种不同的类型,其空间分布与地形地貌、冻土环境条件和发育过程相关;(2)热融滑塌演化过程经历了地表裂缝、活动层剥离滑动、多旋回性退缩和逐渐趋于稳定等4个阶段,主要受到地下冰和极端气候事件影响;(3)热融滑塌失稳是热-水-力场相互作用的结果,应力场作用下影响水热传导,温度场和水分场决定空隙水压力来影响应力场,改变边坡稳定性;(4)极限平衡、数值模拟和不确定性是主要的冻土稳定性模拟方法,各有优缺点.本研究有助于认识和理解热融滑塌的现象和过程,对揭示冻土-气候-地貌交互机制具有重要意义,为寒区地貌学、冻土力学等学科理论体系的完善提供支撑.Abstract: Under global climate warming scenarios, permafrost degradation has triggered retrogressive thaw slumps, posing threats to engineering infrastructure and ecological security in cold regions. However, many scholars lack sufficient understanding of the morphological characteristics and evolutionary processes of RTSs (retrogressive thaw slumps), and the applicability of simulation models has not been systematically summarized. In this study, RTSs from four perspectives: morphology, evolution, destabilization mechanisms, and simulation methods, based on field investigation and literature analysis. The main findings include: (1) The morphological characteristics of RTSs can be classified into 11 types, and their spatial distribution is associated with topographic features, permafrost conditions, and developmental stages. (2) The evolution of RTSs experiences four stages: surface cracking, active layer detachment, polycyclic recession, and gradual stabilization, mainly affected by ground ice and extreme climatic events. (3) The instability of RTSs is the result of the interaction among thermal-hydrological-mechanical fields. Under the influence of the stress field, moisture and heat transfer are affected, while the temperature and moisture fields determine the pore water pressure, which in turn influences the stress field and change slope stability. (4) The limit equilibrium method, numerical simulation, and uncertainty analysis are the main methods for simulating permafrost stability, each with its own advantages and limitations. This study enhances the understanding of the phenomena and processes of RTSs. It is of great significance for revealing the interaction mechanisms among permafrost, climate, and geomorphology, and provides support for the improvement of theoretical frameworks in cold-region geomorphology, permafrost mechanics, and related disciplines.
-
图 3 青藏高原与北极地区活动层剥离和热融滑塌
a.温泉地区活动层剥离; b.温泉地区热融滑塌; c.风火山热融滑塌; d.祁连山热融滑塌; e.加拿大赫歇尔岛海岸侵蚀热融滑塌(Obu et al., 2016); f.阿拉斯加热融滑塌(Balser et al., 2014)
Fig. 3. Active layer detachment and retrogressive thaw slumps on the Qinghai-Tibet Plateau and Arctic region
表 1 部分冻土区热融滑塌发育情况
Table 1. Development status of retrogressive thaw slumps in some permafrost regions
地区 时间跨度(a) 后壁退缩速率(m/a) 面积扩张速率(m2/a) 参考文献 祁连山北部 2009—2017 1.81 5~290 Mu et al.(2020) 风火山北部 1974—1985 2.7 - 王绍令(1990) 北麓河以南可可西里以北 2011—2013 1.83 46 Niu et al.(2012) 阿拉斯加诺阿塔克河流域 2011—2012 11.78 - Swanson and Nolan(2018) 加拿大育空地区 1952—2000 0.45~0.61 Lantuit and Pollard(2008) 表 2 冻土边坡稳定性分析方法
Table 2. Methods for analyzing the stability of permafrost slopes
方法名称 应用领域 定性分析法 历史分析法、图解法、过程机制分析法、岩体质量分析法、工程类比法等 初级工程勘察设计阶段使用 定量分析法 确定性分析方法 刚体极限平衡法、数值分析法 高级的工程勘察设计阶段使用 不确定性分析方法 可靠度评价法、人工神经网络分析法(ANN)、灰色系统评价法、模糊评价法、综合法、遗传算法等 表 3 极限平衡法特点
Table 3. Key features of the limit equilibrium method
名称 分类 原理 优点 缺点 极限平衡法 瑞典条分法、萨尔玛法、詹布法、简化毕肖普法、不平衡推力传递法、斯宾塞法、工程兵团法、摩根斯顿-普莱斯法 假定边坡的岩土体破坏是由于边坡内产生了滑动面,部分坡体沿滑动面滑动而造成的.根据具体情况选择合理的满足摩尔-库伦准则的滑动面.由静力平衡关系,得出滑动时的破坏荷载和最危险滑动面 模型简单、计算简捷,在不能给出应力作用下的结构图像的情况下,仍能对结构的稳定性给出较精确的结论.分析失稳边坡反算的强度参数与室内试验吻合度较好,使分析程序更加可信 近似假设多,且假设与实际情况不一致;没有考虑材料的应力-应变关系;需要先知道滑动面的大致位置和形状,但是滑动面的位置难以准确确定;所得安全系数只是假定滑裂面上的平均安全度 表 4 极限平衡法计算方法
Table 4. Methods for limit equilibrium calculations
年份(a) 作者 稳定性计算公式 公式说明 1974 Hutchinson(1974) $ {F}_{\mathrm{s}}=\frac{2{\mathrm{C}}_{\mathrm{u}}}{\mathit{\gamma }\mathrm{Z}\mathrm{s}\mathrm{i}\mathrm{n}2\mathrm{\beta }} $ 总应力分析法,其认为由于冻结锋面碎块冰集聚导致融化时土体含水量增加,土的不排水抗剪强度降低,从而引发斜坡失稳 1969 Week(1969) $ {F}_{s}= $(1-$ \frac{{\gamma }_{w}{D}_{w}}{\gamma Z} $)$ \frac{\mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\text{'}}}{\mathrm{t}\mathrm{a}\mathrm{n}\beta }+\frac{2{C}^{\text{'}}}{\gamma Z\mathrm{s}\mathrm{i}\mathrm{n}\beta } $ 用“冰堵法”分析Vestspitsbergen冻土斜坡稳定性,提出基于“冰阻渗流”引起孔隙水压力增加机理的有效应力分析法,他们主要考虑土体孔隙水压力增大致使土体有效应力减小而土体强度减弱失稳的情况 1972 Chandler (1972) $ {F}_{s}=\frac{(1-{\gamma }_{u})\mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\text{'}}}{\left[Ka\right(1-{\gamma }_{u})+{\gamma }_{u}]\mathrm{t}\mathrm{a}\mathrm{n}\beta } $ 考虑表层土的主动土压力 1974 Mcroberts and Morgenstern(1974) $ {F}_{s}=\frac{{\gamma }_{s}^{\text{'}}}{{\gamma }_{s}}(1-\frac{1}{1+\frac{1}{2{R}^{2}}} $)$ \frac{\mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\text{'}}}{\mathrm{t}\mathrm{a}\mathrm{n}\beta } $ 提出的基于有效应力和融化-固结理论,认为在斜坡冻土融化-固结过程中,易滑面上超孔隙水压力增加并可引发斜坡失稳 1980 Vallejo(1980) $ {F}_{s}=\frac{({\gamma }_{s}-{\gamma }_{f})CZcos\beta \mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\text{'}}}{[{\gamma }_{f}+({\gamma }_{s}-{\gamma }_{f}\left)C\right]Z\mathrm{s}\mathrm{i}\mathrm{n}\beta } $ 斜坡稳定性计算中滑体成分分为两个方面, 即由大块体和除大块体外的似流体,其稳定性系数与大块体所占总体积多少相关.为此推导了基于土体结构性和有效内摩擦角的评价方法 2004 靳德武和牛富俊(2004) $ \begin{gathered} {F}_{s}= \\ \frac{{C}^{\text{'}}+\left\{\left[\right(1-m)\gamma +m({\gamma }_{sat}-{\gamma }_{w}\left)\right]\right\}z\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\alpha \mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\text{'}}}{\left[\right(1-m)\gamma +m{\gamma }_{sat}]z\mathrm{s}\mathrm{i}\mathrm{n}\alpha \mathrm{c}\mathrm{o}\mathrm{s}\alpha } \end{gathered}$ 应用无限斜坡分析方法.考虑渗流方向与斜坡方向一致的情况,应用有效应力原理,推导出不同含水条件下融冻泥流型滑坡安全系数的解析表达式 2005 沈宇鹏等(2005) $ {F}_{s}=\frac{{\gamma }_{2}h(1-{R}^{\text{'}\text{'}})+{\gamma }_{1}^{\text{'}}Z(1-{P}_{1}+{P}_{2})}{{\gamma }_{2}h+{\gamma }_{1}Z} $
$ {R}^{\text{'}\text{'}} $=$ \frac{erf\left(R\right)}{\left[erf\right(R)+\frac{{e}^{-{R}^{2}}}{R\sqrt[]{\pi }}]} $提出冻土斜坡失稳主要原因是斜坡中的孔隙水压力,并将非饱和理论运用到正融冻土斜坡稳定性分析上,引用孔隙水压力P1和孔隙气压力P2表达在冻土边坡稳定性计算上,提出相应的冻土斜坡稳定分析方法 2006 刘红军和王丕祥(2006) $ {F}_{s}=\frac{{C}^{\text{'}}+\left[\right(1-n)\gamma +n{\gamma }^{\text{'}}]h\mathrm{c}\mathrm{o}\mathrm{s}\alpha \mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\text{'}}}{\left[\right(1-n)\gamma +n{\gamma }_{sat}]h\mathrm{s}\mathrm{i}\mathrm{n}\alpha } $ 考虑地下水渗流作用的情况下运用有效应力法分析土质边坡失稳的主要原因,同时将该方法引入到求解季节性冻土边坡的安全系数的实例中.但是,文章考虑了在渗流情况下渗流力的作用,而未考虑孔隙水压力变化对边坡稳定性影响.此为,在计算渗透力时将水力梯度看成是坡度的参数,然而该参数应由实际的地质情况计算或者实验得出 注:表4中$ {F}_{s} $表示斜坡稳定系数;$ {\mathrm{C}}_{\mathrm{u}} $表示不排水抗剪强度;$ \mathit{\gamma } $表示土容重;$ \mathrm{Z} $表示融化深度;β表示坡度;$ {\gamma }_{w} $表示水容重;$ {D}_{w} $表示滑动面以上水头高度;$ {\varphi }^{\text{'}} $表示有效内摩擦角;$ {C}^{\text{'}} $表示有效黏聚力;$ {\gamma }_{u} $表示孔隙水压力系数;$ Ka $表示主动土压力系数;$ \frac{{\gamma }_{s}^{\text{'}}}{{\gamma }_{s}} $表示滑坡体单位有效重度与单位总重度的比值;$ R $表示融化固结系数;$ {\gamma }_{s} $表示块体的重度;$ {\gamma }_{f} $表示泥流的重度;$ C $表示块体体积占比;$ Z $表示块体厚度;$ {\gamma }_{sat} $表示土的饱和容重;$ m $表示滑体的饱和度;$ z $表示地下冰埋深;$ \alpha $=$ \frac{d}{\sqrt[]{t}} $其中d是t时刻的融化深度;$ {\gamma }_{2} $表示排水面上的总重度;$ {\gamma }_{1}^{\text{'}} $表示潜水面下土的重度;$ {\gamma }_{1} $表示土的总重度;$ {P}_{1} $表示孔隙水压力;$ {P}_{2} $表示孔隙气压力;$ h $表示冻土层的厚度;$ {R}^{\text{'}\text{'}} $表示由固结和渗流引起的超孔隙水压力的简写;$ erf\left(\right) $表示误差函数. 表 5 数值分析法及应用软件
Table 5. Numerical analysis methods and application software
名称 原理 特点及适用领域 软件 有限元法(FEA) 目前最广泛的数值计算方法,它能满足静力平衡条件、应变相容条件,考虑了岩体的不连续性和非均质性,将无限自由度的结构体转化为有限自由度的等价体系;有限元分析的最大特点就是标准化和规范化, 这种特点使得大规模分析和计算成为可能.有限元方法与其他求解边值问题近似方法的根本区别在于它的近似性仅限于相对小的子域中. 有限元法将函数定义在简单几何形状的单元域上,且不考虑整个定义域的复杂边界条件,能够模拟土体与支护的共同作用.不但能进行线性分析还可以进行非线性分析,但是对大变形求解、应力集中等问题的求解还有待改进. ANSYS、ABAQUS、ADINA、RFPA、3D-σ、MIDAS-GTS、ROCSCIENCE-RS2/3等 有限差分法 其基本思想是先把问题的定义域进行网格剖分,然后在网格点上,按适当的数值微分公式把定解问题中的微商换成差商,从而把原问题离散化为差分格式,进而求出数值解.具有简单、灵活以及通用性强等特点,容易在计算机上实现. 应用广泛但在边坡稳定计算中较少应用. FLAC2D/3D、Massflow等 离散元法 把研究对象分离为刚性元素的集合,使每个元素满足牛顿第二定律,用中心差分的方法求解各元素的运动方程,得到研究对象的整体运动形态. 适用于处理不连续介质、大变形、低应力水平等问题,其主要问题是阻尼选取和迭代收敛性. PFC、UEDE、3DEC、MatDEM等 不连续变形分析法 以自然存在的节理面或断层切割岩体形成不同的块体单元, 以各块体的位移作为未知量, 通过块体间的接触和几何约束形成一个块体系统.将边界条件和接触条件等一同施加到总体平衡方程.求解方程组即可得到块体当前时步的位移场、应力场、应变场及块体间的作用力. 可以模拟出岩石块体的移动、转动、张开、闭合等全部过程并据此判断岩体的破坏程度、破坏范围, 从而对岩体的整体和局部稳定性做出正确的评价. DDA 块体理论法 将岩体视为由大量岩块构成的集合体,并对其进行平衡稳定分析的理论.块体理论的核心就是找出临空面上的关键块体.所谓关键块体,即在外荷载和块体自重作用下,由于滑移面上的抗剪强度不足以抵御滑动力而将失稳的块体.在块体理论中先运用有限性定理判别块体是否有限,运用可动性定理判别块体是否可动. 块体理论概念清楚,方法简单,运用起来十分方便,适合于块状结构岩体的稳定分析.它的不足之处是只考虑了岩块的平衡条件,没有考虑岩块和结构面的变形.在块体理论的基础上,又先后出现了一些分析岩体稳定性问题的方法,如块体单元法和DDA(非连续变形分析)法等. BT、BSA3D等 数值流形元法(NMM) 该方法将基于连续介质力学的有限单元法和基于不连续介质力学的非连续变形分析理论统一起来, 创造性地提出相互独立的数学覆盖和物理覆盖双层覆盖系统, 形成任意形状的流形单元. 具有统一处理连续和不连续介质问题的能力, 同时对解决节理岩体的几何大位移、动力及动静交叉等问题有其自身的特点. 极限分析法 所谓有限元极限分析法,就是在弹塑性有限元模型中,通过强度降低或者增大荷载和弹性数值计算,使模型达到极限破坏状态,从而获得模型的破坏状态和相应的安全系数. 能够对具有复杂地质、地貌的岩土工程进行计算;考虑了土体的非线性弹塑性本构关系,以及变形对应力的影响;求解安全系数时,可以不假定滑移面的形状、不进行条分;能模拟土坡失稳过程及其滑移面形状.滑移面大致在水平位移突变的地方及塑性变形发展严重的部位,呈条带状;动面与稳定安全系数;能模拟土体与支护的共同作用. OptumG2/G3 边界元法 将描述数学物理问题、力学问题的偏微分方程边值问题,化为边界积分方程,边界元法只在求解域的边界.上进行离散;边界元法在域内采用了物理问题或弹性力学的基本解和一些积分运算,数值计算只在边界上进行,它属于半解析半数值方法. 求解各种力学和非力学问题、线性和非线性问题等;具有解析与数值相结合的特点,通常具有较高的精度;便于处理无限域以及半无限域问题;缺点是需要事先知道控制微分方程的基本解且在处理材料非线性问题时不如有限元法好,不能处理大变形问题;它的应用范围以存在相应微分算子的基本解为前提,对于非均匀介质等问题难以应用. BEASY、ROCSCIENCE、EXAMINE3D等 物质点法 采用拉格朗日质点和欧拉网格的双重描述,它将连续体离散成一组质点.每个质点代表一块材料区域并携带该材料区域的所有物质信息,如质量、速度、应力和应变等,因此所有质点的集合代表了整个材料区域.计算网格仅用于动量方程的求解和空间导数的计算,它不携带任何物质信息. 发挥了拉格朗日法和欧拉法各自的长处,克服了其弱点,特别适合分析具有超大变形和移动界面的问题,如动态断裂问题、高速碰撞问题和流固耦合问题等. MPM 有限元法-极限平衡法联合法 有限元法没有对滑动面的形式和位置做任何假定, 通过容重增加法或强度折减法确定滑动面的位置和形式,然后用刚体极限平衡法计算安全系数. 不仅考虑了土体的应力-应变关系, 同时能很方便计算出土坡稳定的安全系数.避免了极限平衡法单独计算时反复试算这一过程.这两种方法联合应用可以互相补充, 充分发挥了两者各自的优点. GEO-SLOPE、ROCSCIENCE_SLIDE、理正边坡、GEO5库仑岩土、SlopeLE 2.7 有限元法-离散元耦合法 根据已有的非连续面划分离散块体, 每个离散块体被当成可变形的连续体, 分别划分有限元网格, 块体的运动及相互作用采用与DEM相同的处理方式, 也即单个块体的运动根据该块体所受的不平衡力或不平衡力矩按牛顿第二定律来确定, 并根据接触本构确定块体之间的相互作用.块体之间不需要满足变形协调条件, 块体可以发生平移和旋转. 有限元/离散元(FEM/DEM)耦合分析方法结合连续和非连续数值方法的优点, 不但可以对完整岩体以及已有的不连续面进行很好的模拟, 而且在采用断裂力学的相关准则后, 可以对裂纹的产生和扩展进行模拟. CDEM、GDEM等 -
Abrahams, A. D., Li, G., Parsons, A. J., 1996. Rill Hydraulics on a Semiarid Hillslope, Southern Arizona. Earth Surface Processes and Landforms, 21(1): 35-47. Balser, A. W., Jones, J. B., Gens, R., 2014. Timing of Retrogressive Thaw Slump Initiation in the Noatak Basin, Northwest Alaska, USA. Journal of Geophysical Research: Earth Surface, 119(5): 1106-1120. https://doi.org/10.1002/2013JF002889 Brooker, A., Fraser, R. H., Olthof, I., et al., 2014. Mapping the Activity and Evolution of Retrogressive Thaw Slumps by Tasselled Cap Trend Analysis of a Landsat Satellite Image Stack. Permafrost and Periglacial Processes, 25(4): 243-256. https://doi.org/10.1002/ppp.1819 Burn, C. R., Friele, P. A., 1989. Geomorphology, Vegetation Succession, Soil Characteristics and Permafrost in Retrogressive Thaw Slumps near Mayo, Yukon Territory. Arctic, 42(1): 31-40. Burn, C. R., Lewkowicz, A. G., 1990. Canadian Landform Examples-17 Retrogressive Thaw Slumps. Canadian Geographies / Géographies Canadiennes, 34(3): 273-276. https://doi.org/10.1111/j.1541-0064.1990.tb01092.x Campanella, R. G., Mitchell, J. K., 1968. Influence of Temperature Variations on Soil Behavior. Journal of the Soil Mechanics and Foundations Division, 94(3): 709-734. https://doi.org/10.1061/jsfeaq.0001136 Chandler, R. J., 1972. Periglacial Mudslides in Vestspitsbergen and Their Bearing on the Origin of Fossil 'Solifluction' Shears in Low Angled Clay Slopes. Quarterly Journal of Engineering Geology, 5(3): 223-241. https://doi.org/10.1144/gsl.qjeg.1972.005.03.02 Chen, X., Liu, J. K., Xie, N., et al., 2015. Probabilistic Analysis of Embankment Slope Stability in Frozen Ground Regions Based on Random Finite Element Method. Sciences in Cold and Arid Regions, 7(4): 354-364. Chen, Y. C., 2006. Preliminary Study on Rock and Soil Slope Stability under the Freezing-Thawing Condition (Dissertation). Xi'an University of Science and Technology, Xi'an (in Chinese with English abstract). Cheng, G. D., 1982. The Formation of Thick Layers of Underground Ice. Science in China (Ser. B), 12(3): 281-288 (in Chinese). Cheng, Y. C., Ge, Q., He, F., 2010. Experimental Research on Critical Depth of Slip Surface of Soil Slope in Seasonal Frozen Area. Rock and Soil Mechanics, 31(4): 1042-1046 (in Chinese with English abstract). Cui, K., Qin, X. T., 2023. Landslide Risk Assessment of Frozen Soil Slope in Qinghai Tibet Plateau during Spring Thawing Period under the Coupling Effect of Moisture and Heat. Natural Hazards, 115(3): 2399-2416. https://doi.org/10.1007/s11069-022-05646-8. Drucker, D. C., Prager, W., 1952. Soil Mechanics and Plastic Analysis or Limit Design. Quarterly of Applied Mathematics, 10(2): 157-165. Duan, D. M., Shen, Y. P., Xu, Z. Y., et al., 2008. Stability of the Slope Embankment of Andou Test Section on Qinghai-Tibet Railway in Permafrost Area. China Railway Science, 29(2): 6-11 (in Chinese with English abstract). Fellenius, W. K. A., 1927. Erdstatische Berechnungen Mit Reibung Und Kohäsion (Adhäsion) Und Unter Annahme Kreiszylindrischer Gleitflächen. W. Ernst & Sohn, Berlin. Gong, W. Y., Darrow, M. M., Meyer, F. J., et al., 2019. Reconstructing Movement History of Frozen Debris Lobes in Northern Alaska Using Satellite Radar Interferometry. Remote Sensing of Environment, 221: 722-740. https://doi.org/10.1016/j.rse.2018.12.014. Günther, A., Reichenbach, P., Malet, J. P., et al., 2013. Tier-Based Approaches for Landslide Susceptibility Assessment in Europe. Landslides, 10(5): 529-546. https://doi.org/10.1007/s10346-012-0349-1 Han, B. X., Yin, C., Yuan, W., et al., 2025. Numerical Simulation of the Stability of Frozen Soil Slopes in Permafrost Regions Based on an Enhanced Hydrothermal Coupling Model. Journal of Glaciology and Geocryology, 47(2): 417-429 (in Chinese with English abstract). Hao, J. M., Jia, P. Q., Wu, T. H., et al., 2023. Numerical Analysis of the Impacts of Rainfall on Permafrost-Related Slope Stability on the Qinghai-Tibet Plateau. Journal of Hydrology: Regional Studies, 47: 101439. https://doi.org/10.1016/j.ejrh.2023.101439 Harlan, R. L., 1973. Analysis of Coupled Heat-Fluid Transport in Partially Frozen Soil. Water Resources Research, 9(5): 1314-1323. https://doi.org/10.1029/wr009i005p01314 Harris, C., Rea, B., Davies, M., 2001. Scaled Physical Modelling of Mass Movement Processes on Thawing Slopes. Permafrost and Periglacial Processes, 12(1): 125-135. https://doi.org/10.1002/ppp.373 Hjort, J., Karjalainen, O., Aalto, J., et al., 2018. Degrading Permafrost Puts Arctic Infrastructure at Risk by Mid-Century. Nature Communications, 9: 5147. https://doi.org/10.1038/s41467-018-07557-4 Hutchinson, J. N., 1974. Periglacial Solifluxion: An Approximate Mechanism for Clayey Soils. Géotechnique, 24(3): 438-443. https://doi.org/10.1680/geot.1974.24.3.438 Jiang, L., Wang, L. J., 2008. Stability Study on Swampy Sloping Roadbed in Permafrost Regions of Qinghai-Tibet Railway. Chinese Journal of Geotechnical Engineering, 30(1): 138-142 (in Chinese with English abstract). Jin, D. W., Niu, F. J., Chen, Z. X., et al., 2004. Landslide Hazard from Gelifluction in Qinghai-Tibet Plateau and Stability Analysis Method. Coal Geology & Exploration, 32(3): 49-52(in Chinese with English abstract). Jin, D. W., Sun, J. F., Fu, S. L., 2005. Discussion on Landslides Hazard Mechanism of Two Kinds of Low Angle Slope in Permafrost Region of Qinghai-Tibet Plateau. Rock and Soil Mechanics, 26(5): 774-778 (in Chinese with English abstract). Jin, H. J., Huang, Y. D., Bense, V. F., et al., 2022. Permafrost Degradation and Its Hydrogeological Impacts. Water, 14(3): 372. https://doi.org/10.3390/w14030372 Jin, W. Y., 2019. Coupled Analysis of Water and Heat under Freezing and Thawing Conditions of Soil Slope in Seasonal Frozen Area (Dissertation). Northeast Agricultural University, Harbin (in Chinese with English abstract). Jones, M. K. W., Pollard, W. H., Jones, B. M., 2019. Rapid Initialization of Retrogressive Thaw Slumps in the Canadian High Arctic and Their Response to Climate and Terrain Factors. Environmental Research Letters, 14(5): 055006. https://doi.org/10.1088/1748-9326/ab12fd Kokelj, S. V., Lewkowicz, A. G., 1999. Salinization of Permafrost Terrain Due to Natural Geomorphic Disturbance, Fosheim Peninsula, Ellesmere Island. Arctic, 52(4): 372-385. Kokelj, S. V., Tunnicliffe, J., Lacelle, D., et al., 2015. Increased Precipitation Drives Mega Slump Development and Destabilization of Ice-Rich Permafrost Terrain, Northwestern Canada. Global and Planetary Change, 129: 56-68. https://doi.org/10.1016/j.gloplacha.2015.02.008 Lacelle, D., Bjornson, J., Lauriol, B., 2010. Climatic and Geomorphic Factors Affecting Contemporary (1950-2004) Activity of Retrogressive Thaw Slumps on the Aklavik Plateau, Richardson Mountains, NWT, Canada. Permafrost and Periglacial Processes, 21(1): 1-15. https://doi.org/10.1002/ppp.666 Lantuit, H., Pollard, W. H., 2005. Temporal Stereophotogram-metric Analysis of Retrogressive Thaw Slumps on Herschel Island, Yukon Territory. Natural Hazards and Earth System Sciences, 5(3): 413-423. https://doi.org/10.5194/nhess-5-413-2005 Lantuit, H., Pollard, W. H., 2008. Fifty Years of Coastal Erosion and Retrogressive Thaw Slump Activity on Herschel Island, Southern Beaufort Sea, Yukon Territory, Canada. Geomorphology, 95(1/2): 84-102. https://doi.org/10.1016/j.geomorph.2006.07.040 Lewkowicz, A. G., 1987a. Headwall Retreat of Ground-Ice Slumps, Banks Island, Northwest Territories. Canadian Journal of Earth Sciences, 24(6): 1077-1085. https://doi.org/10.1139/e87-105 Lewkowicz, A. G., 1987b. Nature and Importance of Thermokarst Processes, Sand Hills Moraine, Banks Island, Canada. Geografiska Annaler: Series A, Physical Geography, 69(2): 321-327. https://doi.org/10.1080/04353676.1987.11880218 Lewkowicz, A. G., Harris, C., 2005. Morphology and Geotechnique of Active-Layer Detachment Failures in Discontinuous and Continuous Permafrost, Northern Canada. Geomorphology, 69(1-4): 275-297. https://doi.org/10.1016/j.geomorph.2005.01.011 Lewkowicz, A. G., Way, R. G., 2019. Extremes of Summer Climate Trigger Thousands of Thermokarst Landslides in a High Arctic Environment. Nature Communications, 10: 1329. https://doi.org/10.1038/s41467-019-09314-7 Li, N., Chen, B., Chen, F. X., 2003. Heat - Moisture - Deformation Coupled Model for Composite Foundation in Cold Zone. China Civil Engineering Journal, 36(10): 66-71(in Chinese with English abstract). Li, Y., Jin, H. J., Wen, Z., et al., 2022. Stability of Permafrost Slopes: A Review. Journal of Glaciology and Geocryology, 44(1): 203-216 (in Chinese with English abstract). Li, Z. M., 2017. Study on Mechanism of Moisture-Heat-Stress Coupling for Frozen Soil and Engineering Application (Dissertation). Harbin Institute of Technology, Harbin (in Chinese with English abstract). Liang, R. J., 2007. Research on Frozen Soil Water Migration Based on Neural Network Technique (Dissertation). Lanzhou University, Lanzhou (in Chinese with English abstract). Liu, H. J., Wang, P. X., 2006. Stability Analysis of Loss of Stability Caused by Freeze and Melt of Earthen Side Slopes of Highways. Journal of Harbin Institute of Technology, 38(5): 764-766(in Chinese with English abstract). Liu, Z. Y., Chen, J. B., Jin, L., 2014. Development of Slope Stability Evaluation Process of Permafrost Embankment. Science Technology and Engineering, 14(13): 272-277 (in Chinese with English abstract). Luo, D. L., Liu, J., Chen, F. F., et al., 2024. Research Progress and Prospect of Transition Zone in Permafrost. Earth Science, 49(11): 4063-4081 (in Chinese with English abstract). Luo, J., Niu, F. J., Lin, Z. J., et al., 2019. Recent Acceleration of Thaw Slumping in Permafrost Terrain of Qinghai-Tibet Plateau: An Example from the Beiluhe Region. Geomorphology, 341: 79-85. https://doi.org/10.1016/j.geomorph.2019.05.020 Luo, J., Niu, F. J., Lin, Z. J., et al., 2022. Inventory and Frequency of Retrogressive Thaw Slumps in Permafrost Region of the Qinghai-Tibet Plateau. Geophysical Research Letters, 49(23): e2022GL099829. https://doi.org/10.1029/2022GL099829 Ma, W. D., Liu, F. G., Zhou, Q., et al., 2020. Characteristics of Extreme Precipitation over the Qinghai-Tibet Plateau from 1961 to 2017. Journal of Natural Resources, 35(12): 3039-3050 (in Chinese with English abstract). Mamot, P., Weber, S., Eppinger, S., et al., 2021. A Temperature-Dependent Mechanical Model to Assess the Stability of Degrading Permafrost Rock Slopes. Earth Surface Dynamics, 9(5): 1125-1151. https://doi.org/10.5194/esurf-9-1125-2021 Mao, X. S., Li, N., Wang, B. G., et al., 2006. Coupling Model and Numerical Simulation of Moisture-Heat-Stress Fields in Permafrost Embankment. Journal of Chang'an University (Natural Science Edition), 26(4): 16-19, 62(in Chinese with English abstract). McRoberts, E. C., Morgenstern, N. R., 1974. The Stability of Thawing Slopes. Canadian Geotechnical Journal, 11(4): 447-469. https://doi.org/10.1139/t74-052 Mu, C. C., Shang, J. G., Zhang, T. J., et al., 2020. Acceleration of Thaw Slump during 1997-2017 in the Qilian Mountains of the Northern Qinghai-Tibetan Plateau. Landslides, 17(5): 1051-1062. https://doi.org/10.1007/s10346-020-01344-3 Mu, C. C., Zhang, T. J., Cao, B., et al., 2013. Study of the Organic Carbon Storage in the Active Layer of Permafrost over the Eboling Mountain in the Upper Reaches of the Heihe River in the Eastern Qilian Mountains. Journal of Glaciology and Geocryology, 35(1): 1-9 (in Chinese with English abstract). Nan, Z. T., Li, S. X., Cheng, G. D., 2004. Prediction of Permafrost Distribution on the Qinghai-Tibet Plateau in the Next 50 and 100 Years. Science China: Earth Sciences, 34(6): 528-534 (in Chinese). Nesterova, N., Leibman, M., Kizyakov, A., et al., 2024. Review Article: Retrogressive Thaw Slump Characteristics and Terminology. The Cryosphere, 18(10): 4787-4810. https://doi.org/10.5194/tc-18-4787-2024 Niu, F. J., Luo, J., Lin, Z. J., et al., 2012. Development and Thermal Regime of a Thaw Slump in the Qinghai-Tibet Plateau. Cold Regions Science and Technology, 83/84: 131-138. https://doi.org/10.1016/j.coldregions.2012.07.007 Niu, F. J., Ma, L. F., Jin, D. W., 2006. Stability Evaluation of Slopes in Permafrost Region. Journal of Geotechnical Investigation & Surveying, 34(6): 1-3, 17(in Chinese with English abstract). Nomleni, I. A., Hung, W. Y., Soegianto, D. P., 2023. Dynamic Performance of Root-Reinforced Slopes by Centrifuge Modeling Tests. Landslides, 20(6): 1187-1210. https://doi.org/10.1007/s10346-023-02035-5 O'Neill, K., Miller, R. D., 1985. Exploration of a Rigid Ice Model of Frost Heave. Water Resources Research, 21(3): 281-296. https://doi.org/10.1029/wr021i003p00281 Obu, J., Lantuit, H., Fritz, M., et al., 2016. Relation between Planimetric and Volumetric Measurements of Permafrost Coast Erosion: A Case Study from Herschel Island, Western Canadian Arctic. Polar Research, 35(1): 30313. https://doi.org/10.3402/polar.v35.30313 Pepin, N., Bradley, R. S., Diaz, H. F., et al., 2015. Elevation-Dependent Warming in Mountain Regions of the World. Nature Climate Change, 5(5): 424-430. https://doi.org/10.1038/nclimate2563 Philip, J., De Vries, D. D., 1957. Moisture Movement in Porous Materials under Temperature Gradients. Eos, Transactions American Geophysical Union, 38(2): 222-232. https://doi.org/10.1029/TR038i002p00222 Pufahl, D. E., Morgenstern, N. R., 1979. Stabilization of Planar Landslides in Permafrost. Canadian Geotechnical Journal, 16(4): 734-747. https://doi.org/10.1139/t79-081 Qin, Y. H., Wu, T. H., Zhao, L., et al., 2017. Numerical Modeling of the Active Layer Thickness and Permafrost Thermal State across Qinghai-Tibetan Plateau. Journal of Geophysical Research: Atmospheres, 122(21): 11, 604-11, 620. https://doi.org/10.1002/2017JD026858 Santander, R. E., Bubnovich, V., 2002. Assessment of Mass and Heat Transfer Mechanisms in Unsaturated Soil. International Communications in Heat and Mass Transfer, 29(4): 531-545. https://doi.org/10.1016/S0735-1933(02)00350-0 Shen, Y. P., Xu, Z. Y., Wang, L. J., 2005. Analysis of Stability of Thawing Slopes on Roadbed of Qing-Tibet Railway. China Safety Science Journal, 15(7): 97-100 (in Chinese with English abstract). Song, Y. Q., Zheng, J. J., Li, X. S., et al., 2020. Effects of Freezing-Thawing Cycles on Stability of Soil Slope. Science Technology and Engineering, 20(19): 7885-7890(in Chinese with English abstract). Sordo, B., Rathje, E., Kumar, K., 2024. Sequential Hybrid Finite Element and Material Point Method to Simulate Slope Failures. Computers and Geotechnics, 173: 106525. https://doi.org/10.1016/j.compgeo.2024.106525 Swanson, D. K., 2021. Permafrost Thaw-Related Slope Failures in Alaska's Arctic National Parks, C. 1980-2019. Permafrost and Periglacial Processes, 32(3): 392-406. https://doi.org/10.1002/ppp.2098 Swanson, D. K., Nolan, M., 2018. Growth of Retrogressive Thaw Slumps in the Noatak Valley, Alaska, 2010-2016, Measured by Airborne Photogrammetry. Remote Sensing, 10(7): 983. https://doi.org/10.3390/rs10070983 Taber, S., 1930. The Mechanics of Frost Heaving. The Journal of Geology, 38(4): 303-317. Taylor, G. S., Luthin, J. N., 1978. A Model for Coupled Heat and Moisture Transfer during Soil Freezing. Canadian Geotechnical Journal, 15(4): 548-555. https://doi.org/10.1139/t78-058 Teufel, B., Sushama, L., 2019. Abrupt Changes across the Arctic Permafrost Region Endanger Northern Development. Nature Climate Change, 9(11): 858-862. https://doi.org/10.1038/s41558-019-0614-6 Ugai, K., Leshchinsky, D., 1995. Three-Dimensional Limit Equilibrium and Finite Element Analyses: A Comparison of Results. Soils and Foundations, 35(4): 1-7. https://doi.org/10.3208/sandf.35.4_1 Vallejo, L. E., 1980. A New Approach to the Stability Analysis of Thawing Slopes. Canadian Geotechnical Journal, 17(4): 607-612. https://doi.org/10.1139/t80-068 Wang, C., Hu, X. S., Lu, H. J., et al., 2024. Study on Shear Characteristics of Herbs Plant Root-Soil Composite System in Beiluhe Permafrost Regions under Freeze-Thaw Cycles, Qinghai-Tibet Highway, China. Sustainability, 16(7): 2907. https://doi.org/10.3390/su16072907 Wang, L. X., Zhao, L., Zhou, H. Y., et al., 2023. Evidence of Ground Ice Melting Detected by InSAR and In Situ Monitoring over Permafrost Terrain on the Qinghai-Xizang (Tibet) Plateau. Permafrost and Periglacial Processes, 34(1): 52-67. https://doi.org/10.1002/ppp.2171 Wang, M., Meng, S. J., Yuan, X. M., et al., 2018. Research on Freezing-Thawing Correction Coefficients of Shear Strength Parameters of Seasonal Frozen Soil. Chinese Journal of Rock Mechanics and Engineering, 37(Suppl. 1): 3756-3764 (in Chinese with English abstract). Wang, S. L., 1990. Thaw Slumping in Fenghuo Mountain Area along Qinghai-Xizang Highway. Journal of Glaciology and Geocryology, 12(1): 63-70 (in Chinese with English abstract). Wang, W. L., Wang, L. M., Zheng, L., 2013. The Freeze-Thaw Cycling Effects on Slope Stability in Earthquake. Technology for Earthquake Disaster Prevention, 8(2): 156-163 (in Chinese with English abstract). Wang, X. J., Pang, G. J., Yang, M. X., et al., 2017. Evaluation of Climate on the Tibetan Plateau Using ERA-Interim Reanalysis and Gridded Observations during the Period 1979-2012. Quaternary International, 444: 76-86. https://doi.org/10.1016/j.quaint.2016.12.041 Weeks, A. G., 1969. The Stability of Natural Slopes in South-East England as Affected by Periglacial Activity. Quarterly Journal of Engineering Geology, 2(1): 49-61. https://doi.org/10.1144/gsl.qjeg.1969.002.01.04 Wu, H., Gao, W., Wang, G. F., et al., 2005. Study on Causes of Slide and Stability Technology of Artifical Soil-Cutting Side Slope in Frost Area. Journal of Heilongjiang Institute of Technology, 19(2): 1-4(in Chinese with English abstract). Wu, T. H., 1984. Soil Movements on Permafrost Slopes near Fairbanks, Alaska. Canadian Geotechnical Journal, 21(4): 699-709. https://doi.org/10.1139/t84-076 Xu, J., Yang, G. S., Liu, H., 2007. Evaluation of Permafrost Slope with Monte Carlo Simulation Method and Program Design. Chinese Journal of Underground Space and Engineering, 3(Suppl. 2): 1433-1437 (in Chinese with English abstract). Zhang, S. J., Lai, Y. M., Li, S. Y., et al., 2008. Dynamic Strength of Frozen Soils. Chinese Journal of Geotechnical Engineering, 30(4): 595-599 (in Chinese with English abstract). Zhang, T. J., 2005. Influence of the Seasonal Snow Cover on the Ground Thermal Regime: an Overview. Reviews of Geophysics, 43(4): 2004RG000157. https://doi.org/10.1029/2004RG000157 Zhang, Y. S., Chang, M. J., Liu, Y. H., et al., 2025. Cut Slope Stability Prediction in Permafrost Region Based on Ensemble Learning. Journal of Highway and Transportation Research and Development, 42(1): 131-139(in Chinese with English abstract). Zhang, Y., Dong, J. H., Dong, X. G., et al., 2017. Analysis of Freezing and Thawing of Slope Improved by Soil Nailing Structure in Seasonal Frozen Soil Region. Rock and Soil Mechanics, 38(2): 574-582(in Chinese with English abstract). Zhang, Y., Michalowski, R. L., 2015. Thermal-Hydro-Mechanical Analysis of Frost Heave and Thaw Settlement. Journal of Geotechnical and Geoenvironmental Engineering, 141(7): 04015027. https://doi.org/10.1061/(asce)gt.1943-5606.0001305 Zhao, G., 2010. Mechanism of Shallow Slide on Highway Cutting Slope during Spring in Cold Region (Dissertation). Harbin Institute of Technology, Harbin (in Chinese with English abstract). Zhao, L., Wu, Q. B., Marchenko, S. S., et al., 2010. Thermal State of Permafrost and Active Layer in Central Asia during the International Polar Year. Permafrost and Periglacial Processes, 21(2): 198-207. https://doi.org/10.1002/ppp.688 Zheng, Y. R., 2012. Development and Application of Numerical Limit Analysis for Geological Materials. Chinese Journal of Rock Mechanics and Engineering, 31(7): 1297-1316 (in Chinese with English abstract). Zhou, B., Zhang, Y. L., Wei, S., et al., 2022. Slope Instability Analysis in Permafrost Regions by Shear Strength Parameters and Numerical Simulation. Sustainability, 14(15): 9401. https://doi.org/10.3390/su14159401 陈玉超, 2006. 冻融环境下岩土边坡稳定性研究初探(硕士学位论文). 西安: 西安科技大学. 程国栋, 1982. 厚层地下冰的形成过程. 中国科学(B辑), (3): 281-288. 程永春, 葛琪, 何锋, 2010. 季冻区土质边坡滑动界面临界深度的试验研究. 岩土力学, 31(4): 1042-1046. 段东明, 沈宇鹏, 许兆义, 等, 2008. 青藏铁路安多试验段多年冻土斜坡路基的稳定性. 中国铁道科学, 29(2): 6-11. 韩炳鑫, 尹超, 袁维, 等, 2025. 基于改进水热耦合模型的冻土边坡稳定性数值模拟. 冰川冻土, 47(2): 417-429. 姜龙, 王连俊, 2008. 青藏铁路多年冻土区沼泽化斜坡路基稳定性研究. 岩土工程学报, 30(1): 138-142. 靳德武, 牛富俊, 陈志新, 等, 2004. 青藏高原融冻泥流型滑坡灾害及其稳定性评价方法. 煤田地质与勘探, 32(3): 49-52. 靳德武, 孙剑锋, 付少兰, 2005. 青藏高原多年冻土区两类低角度滑坡灾害形成机理探讨. 岩土力学, 26(5): 774-778. 靳婉莹, 2019. 季冻区渠道土质边坡冻融条件下水热耦合分析(硕士学位论文). 哈尔滨: 东北农业大学. 李宁, 陈波, 陈飞熊, 2003. 寒区复合地基的温度场、水分场与变形场三场耦合模型. 土木工程学报, 36(10): 66-71. 李艳, 金会军, 温智, 等, 2022. 多年冻土区斜坡稳定性研究综述. 冰川冻土, 44(1): 203-216. 李智明, 2017. 冻土水热力场耦合机理研究与工程应用(硕士学位论文). 哈尔滨: 哈尔滨工业大学. 梁若筠, 2007. 基于神经网络方法的冻土水分迁移研究(硕士学位论文). 兰州: 兰州大学. 刘红军, 王丕祥, 2006. 公路土质边坡冻融失稳稳定性分析. 哈尔滨工业大学学报, 38(5): 764-766. 刘志云, 陈建兵, 金龙, 2014. 冻土路基边坡稳定性计算程序开发. 科学技术与工程, 14(13): 272-277. 罗栋梁, 刘佳, 陈方方, 等, 2024. 多年冻土过渡带研究进展与展望. 地球科学, 49(11): 4063-4081. doi: 10.3799/dqkx.2024.075 马伟东, 刘峰贵, 周强, 等, 2020.1961—2017年青藏高原极端降水特征分析. 自然资源学报, 35(12): 3039-3050. 毛雪松, 李宁, 王秉纲, 等, 2006. 多年冻土路基水-热-力耦合理论模型及数值模拟. 长安大学学报(自然科学版), 26(4): 16-19, 62. 牟翠翠, 张廷军, 曹斌, 等, 2013. 祁连山区黑河上游俄博岭多年冻土区活动层碳储量研究. 冰川冻土, 35(1): 1-9. 南卓铜, 李述训, 程国栋, 2004. 未来50与100a青藏高原多年冻土变化情景预测. 中国科学(D辑: 地球科学), 34(6): 528-534. 牛富俊, 马立峰, 靳德武, 2006. 多年冻土地区斜坡稳定性评价问题. 工程勘察, 34(6): 1-3, 17. 沈宇鹏, 许兆义, 王连俊, 2005. 青藏铁路路基中正融土斜坡稳定性分析. 中国安全科学学报, 15(7): 97-100. 宋彦琦, 郑俊杰, 李向上, 等, 2020. 冻融循环作用对土质边坡稳定性的影响. 科学技术与工程, 20(19): 7885-7890. 王淼, 孟上九, 袁晓铭, 等, 2018. 季冻区典型土类抗剪强度冻融修正系数研究. 岩石力学与工程学报, 37(Suppl. 1): 3756-3764. 王绍令, 1990. 青藏公路风火山地区的热融滑塌. 冰川冻土, 12(1): 63-70. 王文丽, 王兰民, 郑龙, 2013. 冻融循环作用下边坡地震动稳定性研究. 震灾防御技术, 8(2): 156-163. 武鹤, 高伟, 王国峰, 等, 2005. 寒区路堑人工土质边坡滑塌原因与稳定技术研究. 黑龙江工程学院学报, 19(2): 1-4. 徐江, 杨更社, 刘慧, 2007. 基于蒙特卡洛模拟法的冻土边坡可靠度评价. 地下空间与工程学报, 3(S2): 1433-1437. 张淑娟, 赖远明, 李双洋, 等, 2008. 冻土动强度特性试验研究. 岩土工程学报, 30(4): 595-599. 张永顺, 常明军, 刘宇航, 等, 2025. 基于集成学习的多年冻土区路堑边坡稳定性预测. 公路交通科技, 42(1): 131-139. 张媛, 董建华, 董旭光, 等, 2017. 季节性冻土区土钉边坡支护结构冻融反应分析. 岩土力学, 38(2): 574-582, 592. 赵刚, 2010. 寒区高等级公路路堑边坡春季浅层滑塌机理研究(博士学位论文). 哈尔滨: 哈尔滨工业大学. 郑颖人, 2012. 岩土数值极限分析方法的发展与应用. 岩石力学与工程学报, 31(7): 1297-1316. -










 下载:
下载: