Theory on Coupling of Radial Flow in a Confined Aquifer and Bending of Confining Unit
-
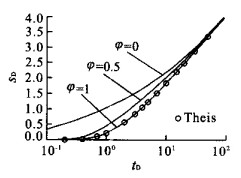
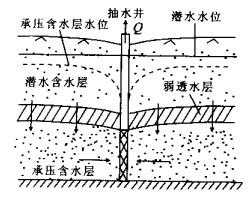
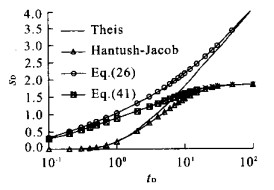
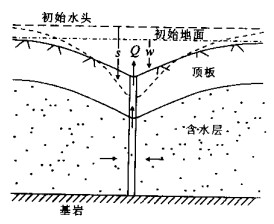
摘要: 指出承压含水层盖层的弯曲变形与开采井周围的径向地下水运动存在相互作用, 而这一效应在传统的井流理论中没有被认识到.通过引入弹性薄板理论, 建立了无越流的承压含水层井流-顶板弯曲效应的解析模型, 同时考虑了含水层和水的压缩性, 结果表明Theis井流方程给出的抽水降深偏小.在此基础上推导了有越流承压含水层井流-盖层弯曲效应的偏微分方程, 求出了解析解, 并与传统理论的结果进行了对比, 表明Hantush-Jacob公式计算的降深也是偏小的.在抽水井附近和抽水初期, 传统理论可能导致显著的相对误差.Abstract: The non-steady radial flow surrounding a pumping well in a fully confined or leaky confined aquifer will induce the bending of confining unit, and then the radial flow patterns are affected by the bending effect through reducing of total stress.However, in conventional theory of groundwater flow, this interaction was omitted. In this study, the elastic plate theory was introduced to establish the analytical models of coupling of radial flow in a confined aquifer and bending of the confining unit, and meanwhile both of non-leaky and leaky conditions were considered as well as the compressibility of skeleton and water. It was indicated by the analytical solutions of the new theory that Theis equation underestimated the drawdown for fully confined aquifers. For leaky confined aquifers, the drawdown simulated by Hantush-Jacob equation was less than that evaluated by the new theory which considered the bending effect of confining unit. The relative errors would be remarkable in the beginning of pumping and/or near the pumping well.
-
Key words:
- radial flow /
- bending /
- confined aquifer /
- leaky /
- analytical solution
-
图 1 无越流承压含水层-井孔模型概化图(箭头表示水流方向)
Fig. 1. Schematic for a fully confined aquifer-well system
图 2 当rD=0.1时, 无越流承压含水层单井定流量抽水的sD-tD曲线
Fig. 2. sD-tD curve for the fully confined aquifer-well systems while rD=0.1
-
[1] Theis C V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground water storage[J]. Trans Ame Geophys, 1935, 16: 519-524. doi: 10.1029/TR016i002p00519 [2] Hsieh P A. Deformation-induced changes in hydraulic head during ground-water withdrawal[J]. Ground Water, 1996, 35(6): 1082-1089. [3] Kim J M, Parizek R R. Numerical simulation of the Noord-bergum effect resulting from groundwater pumping in a layered aquifer system[J]. Journal of Hydrology, 1997, 202(1-4): 231-243. doi: 10.1016/S0022-1694(97)00067-X [4] Burbey T J. Modeling three-dimensional deformation in response to pumping of unconsolidated aquifers[J]. Environmental & Engineering Geosciences, 1999, 5(2): 199-212. [5] Burbey TJ. Stress-strain analyses for aquifer-system characterization[J]. Ground Water, 2001, 39(1): 128-136. doi: 10.1111/j.1745-6584.2001.tb00358.x [6] 陈崇希, 吴修义. 边界附近地下水不稳定井流试验数据的分析法[A]. 综合治理和利用矿床大面积地下水经验汇编[C]. 北京: 煤炭工业出版社, 1979. 22-41.CHEN C X, WU X Y. Analytical methods for pumping tests near boundary[A]. Experiences of controlling and utilizing groundwater in large areas[C]. Beijing: Coal Industry Press, 1979. 22-41. [7] 王旭升, 陈崇希. 改进的Theis井流模型及其解析解———虑含水层顶板的挠曲作用[J]. 地球科学———中国地质大学学报, 2002, 27(2): 199-202. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200202018.htmWANG X S, CHEN C X. Analysis of modified Theis model on well flow: Considering bending of the confining stratum [J]. Earth Science—Journal of China University of Geosciences, 2002, 27(2): 199-202. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200202018.htm [8] Bear J. Dynamics of fluids in porous media[M]. New York: Amer Elsevier Publishing Company, 1972. [9] Arthur P B, Omar M S. Advanced mechanics of materials [M]. New York: John Wiley & Sons Inc, 1985. [10] 陈崇希. 地下水不稳定井流计算方法[M]. 北京: 地质出版社, 1983.CHEN C X. Analytical methods of transient groundwater flow toward wells[M]. Beijing: Geological Publishing House, 1983. [11] 沈观林. 复合材料力学[M]. 北京: 清华大学出版社, 1996.SHEN G L. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 1996. [12] Hantush M S, Jacob C E. Non-steady radial flow in an infinite leaky aquifer[J]. Trans Amer Geophys, 1955, Union 36: 95-100. -
下载:
点击查看大图
图(4)
计量
- 文章访问数: 3684
- HTML全文浏览量: 421
- PDF下载量: 7
- 被引次数: 0
