克立格估计的分析解释与协方差函数的代数确定

边少锋; MenzJoachim

克立格估计的分析解释与协方差函数的代数确定

边少锋¹,
MenzJoachim²

1.
中国科学院测量与地球物理研究所武汉430077
2.
TU Bergakademie Freiberg, 09599 Freiberg, Germany

基金项目: 德国DFG项目“地质统计学模型下的矿山综合评价”; 中国科学院测量与地球物理研究所访问学者基金

详细信息

作者简介:
边少锋, 男, 教授, 1961年生, 1992年毕业于武汉测绘科技大学, 获博士学位, 目前主要从事地球重力场、空间大地测量等研究

中图分类号: P628⁺.2;O212.4
计量
- 文章访问数: 3926
- HTML全文浏览量: 1062
- PDF下载量: 19
- 被引次数: 0
出版历程
- 收稿日期: 1999-01-30
- 刊出日期: 2000-03-25

ANALYTICAL INTERPRETATION TO KRIGING ESTIMATION AND ALGEBRAIC DETERMINATION OF COVARIANCE FUNCTION'S PARAMETER

BIAN Shaofeng¹,
Menz Joachim²

1.
The Surveying and Geophysical Institute of Chinese Academy of Sciences, Wuhan, 430077, China
2.
TU Bergakademie Freiberg, 09599 Freiberg, Germany

摘要

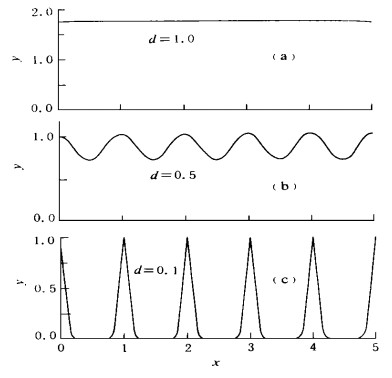
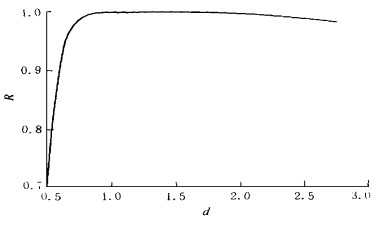
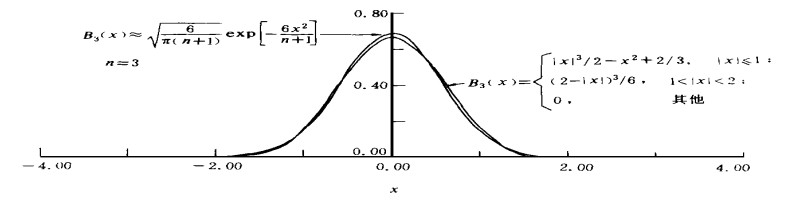
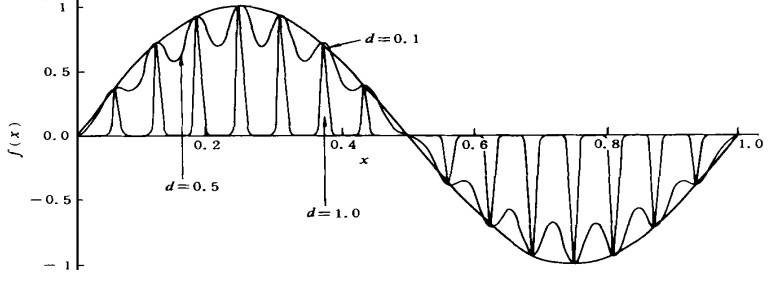
摘要: 首先引入利用旋转面作为基函数的函数逼近概念, 在此基础上经过复杂的矩阵推导证明泛克立格法可表示为传统的带权最小二乘多项式拟合与以旋转面作为基函数的函数逼近, 并在一定条件下(随机场高度连续无块金效应) 论证了协方差(即旋转面) 的参数可通过数学分析的方法确定, 给出了以高斯函数为例确定协方差函数的两个准则.
- 克立格估计 /
- 协方差函数 /
- 地质统计学
Abstract: The analytical interpretation to Kriging estimation and the algebraic determination of a covariance function's parameter are presented. This paper first introduces the concept of function approximation using a rotating surface as a basic function. Then it is demonstrated that the universal Kriging may be expressed as the traditional weighted least square fitting and as the function approximation with a rotating surface as a basic function. It is also demonstrated that the parameter of a covariance function (i.e. a rotating surface) can be determined by the mathematical analysis on a certain condition (i.e. a highly continuous lump goldree effect in a random field). Finally, this paper presents two principles for the determination of a covariance function's parameter with the Gaussian function as an example: one is formulated through analysis of the linear combinations of the shifted Gaussian functions, and the other is derived from the equivalence between Bplines and Gaussian functions.
- Kriging estimation /
- covariance function /
- geostatistics

HTML全文

图 1 不同参数下的Gauss函数

Fig. 1. Gaussian functions with different parameters

下载: 全尺寸图片幻灯片

图 2 Gauss函数的移位线性组合

Fig. 2. Linear combinations of Gaussian functions

下载: 全尺寸图片幻灯片

图 3 比值函数随参数d变化曲线

Fig. 3. The ratio function with respect to the parameter d

下载: 全尺寸图片幻灯片

图 4 n=3时B样条与Gauss函数对比

Fig. 4. Comparison between a Gaussian function and its equivalent cubic spline

下载: 全尺寸图片幻灯片

图 5 d=0.1, d=0.5和d=1.0时Gauss函数逼近正弦曲线示意图

Fig. 5. Approximated sine curve by a Gaussian function with d=0.1, d=0.5 and d=1.0 respectively

下载: 全尺寸图片幻灯片

表 1 不同阶次样条对应的Gauss函数参数

Table 1. Determining parameters of Gaussian functions by splines with different orders

参考文献(6)

[1]	Cressie N. Statistics for spatial data[M]. New York: John Wiley & Sons, 1991.
[2]	Wackernagel H. Multivariate geo-statistics[M]. Heidelberg: Springer-Verlag, 1995.
[3]	Menz J. Anwendung der Geostatistik zur Gebirgs-und Lager-stattengeometrisierung[ M]. TU Bergakademie, Freiberg: Forschungbericht, 1996.
[4]	Martheon G. Splines and Kriging: their formal equivalence in down to earth statistics[A]. In: Merriarn D, ed. Solu- tions looking for geological patterns[ C]. Syracuse Univ Geology Contribution, 1981, 8: 77~97.
[5]	Dubrule O. Comparing splines and Kriging[ J]. Computer & Geosciences, 1984, 10(2): 327~328.
[6]	Unser M, Aldroubi A. Polynomial spline and wavelets: a signal processing perspective[ A]. In: Chui C K, ed. Wavelet: a tutorial in theory and applications[C]. Boston: Academic Press, 1992. 91~123.