MML-EM Algorithm and Its Application on Mixed Distributions of Geochemical Data
-
摘要: 概率图法在筛分混合分布的问题上，只能对混合分布的各项参数作出粗略的估计.为了解决这一问题，引入了MML-EM法.模拟研究表明，在混合分布参数估计上，该方法比概率图法有更高的精度.以江西大吉山钨矿石英脉原生晕数据为例，经过该方法的筛分，得到钨、钽和铌的含量服从由2个子分布组成的混合对数正态分布，即双峰分布.结合前人的地质研究，可以初步得出结论：钨的高值总体代表了岩浆期后热液成矿期的热液充填石英脉型矿化，低值总体可能代表其他成矿期的事件，其中高值部分可能构成岩浆晚期浸染型的弱钨矿化.钽和铌的高值总体代表岩浆晚期的浸染型富矿化，低值总体代表其他成矿期的叠加矿化.该方法为化探数据中混合分布的筛分以及解释多地质成因总体提供了一种良好的定量化工具.Abstract: When separating the mixed distributions of element abundance, probability graphs can only make a rough estimate of parameters. To solve this problem, we introduce a method of Minimum Message Length Criterion-Expectation-Maximization Algorithm (MML-EM). Simulation studies have shown that the method has higher accuracy than probability graphs in estimating the parameters of mixed distributions of element abundance. It is applied to dealing with the geochemical data of quartz vein, sampled from tungsten ore in Dajishan, Jiangxi Province. The research shows that the concentrations of W, Ta and Nb are mixed pairs of log-normal distributions, biomodel distributions. Referring to the previous geological results, the conclusion is as follows. For W, the component with high average value represents the high-grade ore formed by hydrothermal filling type in ore-forming processes, and the one with low average value represents the mineralization in other stages, high-value parts of which may indicate that there is a weak disseminated tungsten mineralization at late magmatic stage. For Ta and Nb, the situation is similar. So the method provides a good quantitative tool that can help separate the mixed distributions of geochemical data and explain the multiple geological events.
-
元素含量的统计分布形式是地球化学的基本事实，也是勘查地球化学技术方法的理论基础.除了正态分布和对数正态分布，实际计算中还经常遇到双峰或多峰的分布总体.
另外，对化探数据作多元统计分析前，通常需要假设样本服从正态分布或对数正态分布.但是，许多情况中样本无法通过假设检验，这可能与样本容量太大、存在异常值和混合分布3种因素有关(Zhang et al., 2005).本文正是从混合分布的角度研究化探数据的分布规律.另外，混合分布在解释多地质成因总体时也具有重要意义(赵鹏大等，1983).
在研究化探数据的分布规律上，前人已经取得很多重要的成果.Allegre and Lewin(1995)对地球化学场元素的分布形式进行了详细的分析，并将其划分为两大类和四大亚类：正态和多模式分布、分形和多重分形分布，并对其形成机制进行了详细的研究，指出正态和多模式分布对应于混合作用占主导地位的地球化学过程，而分形和多重分形分布对应于分异占主导地位的地球化学过程.这里的多模式分布即为混合分布.对于分形和多重分形分布，近年来取得了很多进展，并在应用中起到了重要的作用(Cheng et al., 1994；申维，2008).
然而，对于混合分布，成果相对较少.Sinclair(1991)在研究阈值估计问题时认为，背景值和异常值与不同的地质过程有关，它们具有不同的概率密度函数，包含着这种思想的方法才是解决阈值估计问题的根本途径.但是引入的概率图法(王建康和盖钧镒，1995)在混合分布的筛分上，并不是一个很精确的方法.这一点会在下面详细讨论.
一般的混合模型研究中存在两大难题：第一是怎样估计混合模型的参数；第二是混合模型分支数的确定.对于前者，基于EM算法的极大似然估计是一种有效的参数估计方法，但是EM算法只是一种局部最优搜索算法，常常会陷入局部最优解，这使得它的搜索结果对初始值非常敏感(连军艳，2006).对于模型分支数的确定问题，王建康和盖钧镒(1995)将解决方法分为两类：图形方法和统计检验方法.图形方法只能对参数进行粗略的估计，并且无法估计参数的误差.地质中常常使用的概率图法即属于图形方法.对于统计检验方法，前人也已经做了很多尝试.Hsu et al.(1986)提出了一个基于自助法的逐步过程估计有限分布中的基本分布的数目，但是参数估计却要依赖于基于EM算法的极大似然估计，这也降低了该方法的稳定性.似然比统计量测验是一种被广泛采用的统计推断方法，但是在混合模型中，如何应用该方法一直在探索之中.
本文采用的方法是Figueiredo and Jain(2002)提出的基于最小信息长度准则(Minimum Message Length Criterion，简称MML)和期望最大化法(Expectation-Maximization Algorithm，简称EM)的方法，简称MML-EM方法.该方法真正实现了同时处理分支数和模型参数这2个问题(连军艳，2006)，其特点是它将参数估计与模型分支数的选择紧密结合到一个单一的EM算法中，从而加快了计算速度，克服了原有EM算法的许多缺点，是目前该类算法中表现最好的方法之一.
1. MML-EM方法
不失一般性，假设样本的混合分布模型为：
p(x;θ)=k∑i=1αif(x,θi), 其中，参数集θ=(k, θ1, …, θk, α1, …, αk)，k为分支的个数，f(x, θi)表示第i个分支的概率密度函数，θi为相应的参数，αi为第i个分支的权重，并有$\mathop \sum \limits_{i = 1}^k {\alpha _i} = 1,{\alpha _i} > 0$.
上述数学模型是混合分布的一般公式，研究该模型的目的是精确地估计混合分布的分支数和每个子分布的参数，如权重、均值和方差.
MML-EM方法是以EM算法为基础的更精细的方法.EM算法(张士峰，2004)是一种迭代方法，主要用来求解后验分布的众数(即极大似然估计)，它的每一次迭代由两步组成：E步(求期望)和M步(极大化).其基本思想是在给出缺失数据初值的情况下，估计出模型参数的值；然后再根据参数值估计出缺失数据的值.根据估计出的缺失数据的值再对参数值进行更新，如此反复迭代，直至收敛，迭代结束并得到最优的参数值(连军艳，2006).
基于MML准则和EM框架的算法是这样进行的：第1步和第2步分别是EM算法的E步(求期望)和M步(极大化)，第3步是利用前两步计算的参数计算相应的信息长度.重复上述的3步，直到求出在信息长度最小的情况下最优分支数和分布参数.详细的公式推导和实现算法见文献(Figueiredo and Jain, 2002).
2. MML-EM方法模拟研究
下面利用MATLAB软件生成服从正态分布的随机数，研究MML-EM方法在估计混合正态分布参数时的可行性.该方法适用于研究多元混合分布，本文只考虑一维混合正态分布.设定两组正态分布参数如表 1，其中α表示各个分支的权重，μ和σ表示各个分支的均值和方差，每次试验生成的样本个数为1 000.以试验1为例，先生成500个服从N(0, 1)的随机数，再生成500个服从N(3, 1)的随机数，将这1 000个随机数混合在一起，最后利用MML-EM方法估计出相应的参数.
表 1 MML-EM方法模拟Table Supplementary Table Simulation of the algorithm of MML-EM试验号 α真值 α估计值 μ真值 μ估计值 σ真值 σ估计值 1 0.5 0.51 0 -0.04 1 0.93 0.5 0.49 3 3.00 1 0.86 2 0.9 0.9 0 0 1 1.03 0.1 0.1 6 5.88 1 0.95 设定迭代精度为10-9，分支数的搜索范围是[1, 4]，经过计算得到估计值表 1.作为参照，使用概率图法筛分上述两组随机数，得到表 2.对比表 1和表 2，仍以试验1为例：2个分支的比重都是0.5，MML-EM方法估计得到的比重为0.51和0.49，概率图法得到的是0.6和0.4；2个分支的均值为0和3，MML-EM方法估计得到的为-0.04和3.00，概率图法得到的是0.7和2.3；2个分支的方差都为1，MML-EM方法估计得到的为0.93和0.86，概率图法得到的是1.2和1.08.综上可得，MML-EM方法估计参数的精度更高.
表 2 概率图法模拟Table Supplementary Table Simulation of the probability graphs试验号 α真值 α估计值 μ真值 μ估计值 σ真值 σ估计值 1 0.5 0.6 0 0.7 1 1.2 0.5 0.4 3 2.3 1 1.08 2 0.9 0.67 0 -0.9 1 4.25 0.1 0.33 6 5.1 1 3.8 3. 应用实例
本文以江西省大吉山钨矿的石英脉原生晕数据为例，运用上述方法，对该矿内钨的分布特征进行研究.
大吉山钨矿主要由两类矿床构成：外接触带大脉型石英脉型钨矿床和岩体浸染型钨铍钽铌矿床.据前人研究，矿床的成矿作用具有多期多阶段性.滕建德(1990)对其进行研究，提出了3个成矿期8个成矿阶段的认识，详细情况见表 3.
表 3 大吉山矿床成矿期与成矿阶段Table Supplementary Table Metallogenetic epoches and metallogenetic stages of Dajishan deposit成矿期 成矿阶段 矿物共生组合 蚀变特征 温度(℃) 岩浆期 I1含TR矿化花岗闪长岩 斜长石、微斜长石、条纹长、黑云母、石英、榍石、磁铁矿、独居石、锆石、褐帘石 弱钾长石化 成岩：640 I2含Nb-Ta-TR矿化二云母二长花岗岩 斜长石、微斜长石、条纹长、石英黑云母、白云母、独居石、磷钇矿 钾长石化
弱钠长石化成岩：550；成矿：334 I3含Nb-Ta-Be-W白云母花岗岩 斜长石、微斜长石、白云母、石英、钠长石、石榴子石、绿柱石、硅铍石、铌钽铁矿、细晶石、黑钨矿、白钨矿 钠长石化
白云母化
云英岩化成岩：526；成矿：309 伟晶期 I4含Be-(Rb)-W矿化似伟晶岩 白云母、微斜长石、绿柱石、石英、黑钨矿 无 成岩：503~455；成矿：280~255 岩浆期
后热液
成矿期I5含W-Be-(Rb)长石石英脉 白云母、微斜长石、绿柱石、石英、黑钨矿 白云母化
硅化成矿：290 I6含W-Be-Mo石英脉 白云母、电气石、石英、微斜长石、绿柱石、含铍石榴子石、黑钨矿、辉钼矿 白云母化
电气石化
萤石化成矿：287 I7含W-Mo-Bi石英硫化物脉 白云母、石英、黑钨矿、白钨矿、雌黄铁矿、黄铁矿、毒砂、闪锌矿、方铅矿 白云母化
硅化
萤石化
绢云母化成矿：260 I8含W-碳酸盐脉 白云母、碳酸盐、萤石、黑钨矿、白钨矿、黄铁矿 白云母化碳酸盐化绿泥石化 成矿：130 以成矿元素钨、钽和铌为例，经过MML-EM方法计算得到表 4、5、6和图 1、2、3.需要说明的是，由于混合对数正态分布的直方图很难清晰地显示各个分支，图 1、2、3是对原始数据取自然对数变换后的混合分布筛分图.由表 4和图 1可知，石英脉中钨含量服从由2个子分布组成的混合对数正态分布.结合实际勘查和矿物共生组合分析①，可以得出结论：矿体中钨含量的混合分布代表了两种不同地质成因.其中分支2，平均品位为297.7×10-6，占79%，它代表了浓度克拉克值较高的岩浆期后热液成矿期.由于采集的355个坑道样品中以石英脉型为主，所以该分支实际上反映了第6个和第7个成矿阶段.分支1，平均品位为26.1×10-6，占21%，其中的高值部分可能代表其他成矿期如岩浆晚期浸染型的弱钨矿化，即第3个成矿阶段.
① 张德会等，2009.江西省全南县大吉山钨矿矿产预测项目报告.
表 4 钨的分布参数Table Supplementary Table Estimated statistical parameters of tungsten分支 权重 均值(10-6) 方差 1 0.21 26.1 12.6 2 0.79 297.7 403 表 5 钽的分布参数Table Supplementary Table Estimated statistical parameters of tantalum分支 权重 均值(10-6) 方差 1 0.25 0.01 0.01 2 0.75 1.60 28.0 表 6 铌的分布参数Table Supplementary Table Estimated statistical parameters of niobium分支 权重 均值(10-6) 方差 1 0.95 1.43 3.13 2 0.05 13.38 4.29 
图 1 钨的混合分布筛分(对数变换后)Fig. 1. Tungsten concentration data partitioned into two-components
图 2 钽的混合分布筛分(对数变换后)Fig. 2. Tantalum concentration data partitioned into two-components
图 3 铌的混合分布筛分(对数变换后)Fig. 3. Niobium concentration data partitioned into two-components再分析石英脉中钽和铌的分布规律，见表 5、6和图 2、3.这两种元素虽未构成成矿的主要元素，但是它们的分布总体也都是服从由2个子分布组成的混合对数正态分布.经分析，这也是不同阶段的成矿作用在空间上的叠加造成的.由于岩浆期形成了白云母花岗岩中的岩浆自变质矿物，其中赋存有浸染型的Nb-Ta矿化，所以其中高值总体代表了大吉山另一重要的矿化类型——岩浆期Nb-Ta矿化，即第2个和第3个成矿阶段；而低值总体代表了其他成矿期的弱矿化.
由上可见，矿体品位的混合分布及其筛分常常具有明确的地质意义，可为矿床成因提供重要佐证(赵鹏大，1990).
4. 结论
(1) 模拟研究表明，与概率图法相比，MML-EM方法在估计混合分布参数时具有更高的精度.另外，有MATLAB程序包可实现该方法，使用快捷方便，所以该方法可以广泛推广.
(2) 使用该方法分析江西大吉山钨矿石英脉的原生晕数据，结合前人的地质研究成果，可以初步得到结论：钨、钽和铌的含量都服从由2个子分布组成的混合对数正态分布，它们分别代表了两种不同的地质成因.其中，钨的高值总体，代表岩浆期后热液成矿期的热液充填型矿化，对应于第6个和第7个成矿阶段，即含W-Be-Mo石英脉矿化阶段和含W-Mo-Bi石英硫化物脉矿化阶段；低值总体的高值部分可能代表其他成矿期如岩浆晚期浸染型的弱钨矿化，对应于第3个阶段的Nb-Ta-Be-W矿化；钽和铌的高值总体代表岩浆晚期浸染型矿化，主要对应于第2个和第3个成矿阶段，低值总体代表了其他成矿期的矿化.由此可见，该方法为化探数据中混合分布的筛分以及解释多地质成因总体提供了一种良好的定量化工具.
-
图 1 钨的混合分布筛分(对数变换后)
Fig. 1. Tungsten concentration data partitioned into two-components
图 2 钽的混合分布筛分(对数变换后)
Fig. 2. Tantalum concentration data partitioned into two-components
图 3 铌的混合分布筛分(对数变换后)
Fig. 3. Niobium concentration data partitioned into two-components
表 1 MML-EM方法模拟
Table 1. Simulation of the algorithm of MML-EM
试验号 α真值 α估计值 μ真值 μ估计值 σ真值 σ估计值 1 0.5 0.51 0 -0.04 1 0.93 0.5 0.49 3 3.00 1 0.86 2 0.9 0.9 0 0 1 1.03 0.1 0.1 6 5.88 1 0.95 
下载: 导出CSV
表 2 概率图法模拟
Table 2. Simulation of the probability graphs
试验号 α真值 α估计值 μ真值 μ估计值 σ真值 σ估计值 1 0.5 0.6 0 0.7 1 1.2 0.5 0.4 3 2.3 1 1.08 2 0.9 0.67 0 -0.9 1 4.25 0.1 0.33 6 5.1 1 3.8
下载: 导出CSV
表 3 大吉山矿床成矿期与成矿阶段
Table 3. Metallogenetic epoches and metallogenetic stages of Dajishan deposit
成矿期 成矿阶段 矿物共生组合 蚀变特征 温度(℃) 岩浆期 I1含TR矿化花岗闪长岩 斜长石、微斜长石、条纹长、黑云母、石英、榍石、磁铁矿、独居石、锆石、褐帘石 弱钾长石化 成岩：640 I2含Nb-Ta-TR矿化二云母二长花岗岩 斜长石、微斜长石、条纹长、石英黑云母、白云母、独居石、磷钇矿 钾长石化
弱钠长石化成岩：550；成矿：334 I3含Nb-Ta-Be-W白云母花岗岩 斜长石、微斜长石、白云母、石英、钠长石、石榴子石、绿柱石、硅铍石、铌钽铁矿、细晶石、黑钨矿、白钨矿 钠长石化
白云母化
云英岩化成岩：526；成矿：309 伟晶期 I4含Be-(Rb)-W矿化似伟晶岩 白云母、微斜长石、绿柱石、石英、黑钨矿 无 成岩：503~455；成矿：280~255 岩浆期
后热液
成矿期I5含W-Be-(Rb)长石石英脉 白云母、微斜长石、绿柱石、石英、黑钨矿 白云母化
硅化成矿：290 I6含W-Be-Mo石英脉 白云母、电气石、石英、微斜长石、绿柱石、含铍石榴子石、黑钨矿、辉钼矿 白云母化
电气石化
萤石化成矿：287 I7含W-Mo-Bi石英硫化物脉 白云母、石英、黑钨矿、白钨矿、雌黄铁矿、黄铁矿、毒砂、闪锌矿、方铅矿 白云母化
硅化
萤石化
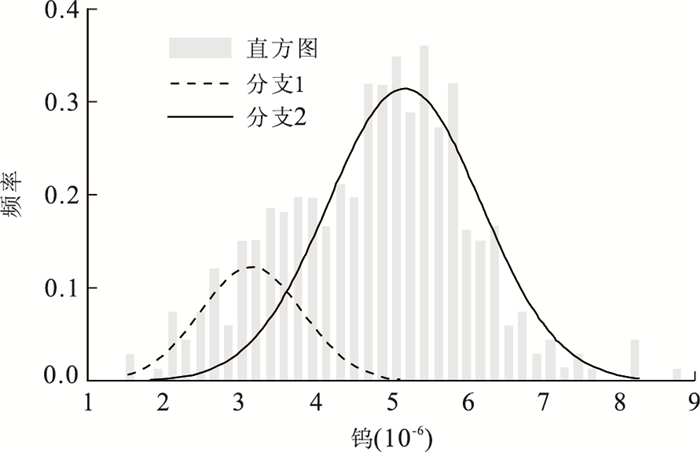
绢云母化成矿：260 I8含W-碳酸盐脉 白云母、碳酸盐、萤石、黑钨矿、白钨矿、黄铁矿 白云母化碳酸盐化绿泥石化 成矿：130
下载: 导出CSV
表 4 钨的分布参数
Table 4. Estimated statistical parameters of tungsten
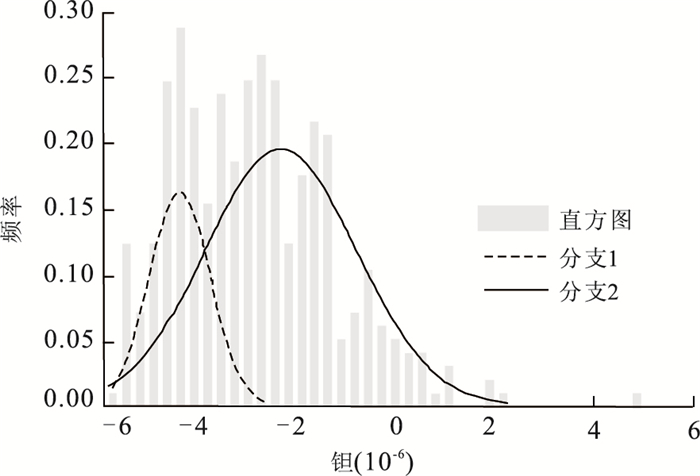
分支 权重 均值(10-6) 方差 1 0.21 26.1 12.6 2 0.79 297.7 403
下载: 导出CSV
表 5 钽的分布参数
Table 5. Estimated statistical parameters of tantalum
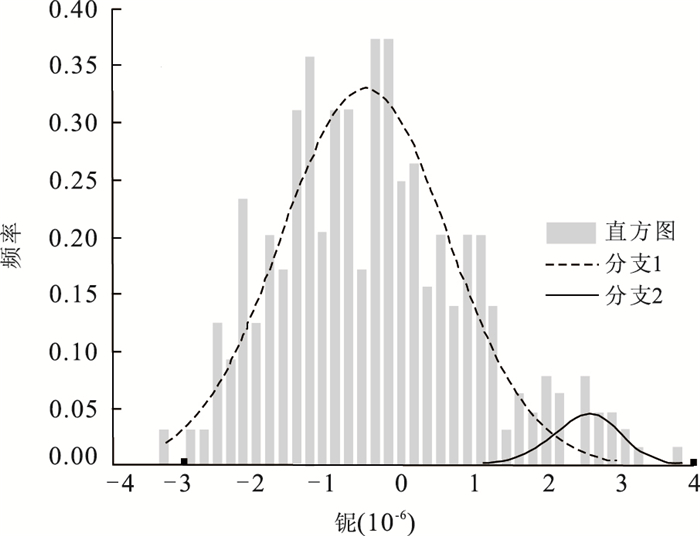
分支 权重 均值(10-6) 方差 1 0.25 0.01 0.01 2 0.75 1.60 28.0
下载: 导出CSV
表 6 铌的分布参数
Table 6. Estimated statistical parameters of niobium
分支 权重 均值(10-6) 方差 1 0.95 1.43 3.13 2 0.05 13.38 4.29
下载: 导出CSV
-
Allegre, C.J., Lewin, E., 1995. Scaling laws and geochemical distributions. Earth and Planetary Science Letters, 132(1-4): 1-13. doi: 10.1016/0012-821X(95)00049-I Cheng, Q.M., Agterberg, F.P., Ballantyne, S.B., 1994. The separation of geochemical anomalies from background by fractal methods. Journal of Geochemical Exploration, 51(2): 109-130. doi: 10.1016/0375-6742(94)90013-2 Figueiredo, M.A.F., Jain, A.K., 2002. Unsupervised learning of finite mixture models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(3): 381-396. doi: 10.1109/34.990138 Hsu, Y.S., Walker, J.J., Ogren, D.E., 1986. A stepwise method for determining the number of component distributions in a mixture. Mathematical Geology, 18(2): 153-160. doi: 10.1007/BF00898280 Lian, J.Y., 2006. Improved EM algorithm and its application on the parameter estimation in mixed distribution models (Dissertation). University of Chang'an, Xi'an (in Chinese with English abstract). Shen, W., 2008. Fractal invariable distribution and its application in gold mineral deposits in Shandong Province, China. Earth Science Frontiers, 15(4): 65-70 (in Chinese with English abstract). http://search.cnki.net/down/default.aspx?filename=DXQY200804009&dbcode=CJFD&year=2008&dflag=pdfdown Sinclair, A.J., 1976. Applications of probability graphs in mineral exploration. Translated by Zhao, P.D., Hu, W.L., Li, Z.J., et al., 1981. Geological Publishing House, Beijing (in Chinese). Sinclair, A.J., 1991. A fundamental approach to threshold estimation in exploration geochemistry: probability plots revisted. Journal of Geochemical Exploration, 41(1-2): 1-22. doi: 10.1016/0375-6742(91)90071-2 Teng, J.D., 1990. Vertical zoning distribution of mineralization in the Dajishan mine. Mining Geology, 11(2): 13-24 (in Chinese). Wang, J.K., Gai, J.Y., 1995. Mixture distribution and its application. Journal of Biomathematics, 10(3): 87-92 (in Chinese with English abstract). http://europepmc.org/abstract/CBA/568584 Zhang, C.S., Manheim, F.T., Hinde, J., et al., 2005. Statistical characterization of a large geochemical database and effect of sample size. Applied Geochemistry, 20(10): 1857-1874. doi: 10.1016/j.apgeochem.2005.06.006 Zhang, S.F., 2004. EM algorithm and its application in parameter estimation for Gussian mixture. Journal of Spacecraft TT & C Technology, 23(4): 47-52 (in Chinese with English abstract). Zhao, P.D., 1990. The statistical analysis of geological exploration. Geological Publishing House, Beijing (in Chinese). Zhao, P.D., Hu, W.L., Li, Z.J., 1983. Statistical prediction of mineral deposit. Geological Publishing House, Beijing (in Chinese). 连军艳, 2006. EM算法及其改进在混合模型参数估计中的应用研究(硕士学位论文). 西安: 长安大学. 申维, 2008. 分形不变分布及其在山东地区金矿床中的应用. 地学前缘, 15(4): 65-70. doi: 10.3321/j.issn:1005-2321.2008.04.008 Sinclair, A.J., 1976. 概率图在矿床勘探中的应用. 赵鹏大, 胡旺亮, 李紫金, 等译, 1981. 北京: 地质出版社. 滕建德, 1990. 大吉山矿区矿化垂直带状分布. 矿山地质, 11(2): 13-24. 王建康, 盖钧镒, 1995. 混合分布理论及应用. 生物数学学报, 10(3): 87-92. https://www.cnki.com.cn/Article/CJFDTOTAL-SWSX199503016.htm 张士峰, 2004. 混合正态分布参数极大似然估计的EM算法. 飞行器测控学报, 23(4): 47-52. 赵鹏大, 1990. 地质勘探中的统计分析. 北京: 地质出版社. 赵鹏大, 胡旺亮, 李紫金, 1983. 矿床统计预测. 北京: 地质出版社. -
下载:
点击查看大图
计量
- 文章访问数: 733
- HTML全文浏览量: 439
- PDF下载量: 31
- 被引次数: 0
