Horizontal Derivative Iteration Method for Downward Continuation of Gravity and Magnetic Data
-
摘要: 向下延拓是重磁数据处理的常用手段，能有效地区分叠加异常、增强浅部异常，但现有向下延拓算法的计算大多是不稳定的，且易受噪声的干扰，往往造成异常形态的畸变.提出一种基于水平导数和向上延拓联合迭代的向下延拓算法，由于向上延拓和水平导数的计算是稳定的，因此该向下延拓方法可有效地增强结果的准确性和稳定性.理论模型试验表明该方法的向下延拓结果比Fourier变换计算结果更加稳定、准确，且受噪音干扰小.将该方法应用于实际数据的处理，结果显示该方法能稳定和准确地完成异常的向下延拓任务，且有效地增强了浅部局部异常.Abstract: Downward continuation is an effective tool in the processing of potential field data, which can identify overlap anomalies and enhance weak anomalies effectively. But the existing computation methods of downward continuation easily distort the true feature of potential field data since they are unstable and sensitive to noise. In this paper, we present an iteration method based on horizontal derivative, and we prove that downward continuation can be computed by the combination of upward continuation and horizontal derivative, and the computation of upward continuation and horizontal derivative is stable, which confirms stability and reliability of the method. The proposed method has been tested on synthetic potential field data, and it is found that the output results are more stable and accurate than those computed by the Fourier transform, and more insensitive to noise. Its application to real potential field data shows the same results and it really enhances the local anomalies.
-
Key words:
- gravity and magnetic /
- horizontal derivative /
- downward continuation /
- iteration /
- geophysics
-
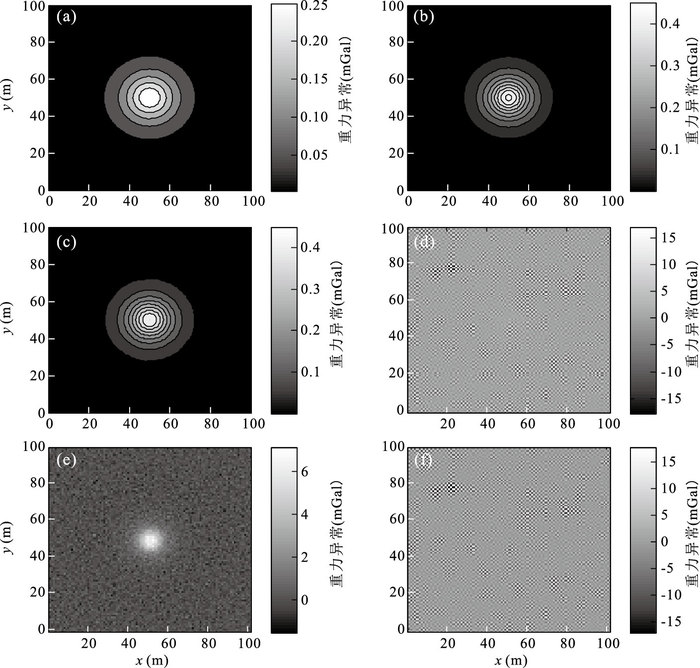
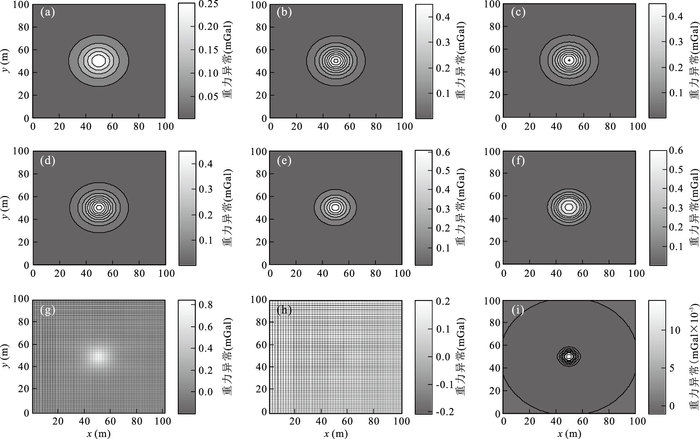
图 1 模型重力异常不同延拓方法应用效果
a.球体埋深为15 m时引起的重力异常；b.球体埋深为12 m时的异常；c.利用本文方法将1a中异常向下延拓3 m；d.利用Fourier变换将1a中异常向下延拓3 m；e.球体埋深为10 m时异常；f.利用本文方法将1a中异常向下延拓5 m；g.利用Fourier变换将1a中异常向下延拓5 m；h.图 1e和1g异常的差；i.图 1e和1h异常的差
Fig. 1. The application effect of different downward continuation methods of synthetic gravity anomaly
图 2 剖面重力异常不同延拓方法应用效果
a.不同方法向下延拓3 m后异常；b.不同方法向下延拓5 m后异常
Fig. 2. The application effect of different downward continuation methods of profile gravity anomaly
-
Abedi, M., Gholami, A., Norouzi, G.H., 2013.A Stabled Downward Continuation of Airborne Magnetic Data:A Case Study for Mineral Prospectively Mapping in Central Iran.Computers & Geosciences, 52:269-280.doi: 10.1016/j.cageo.2012.11.006 Baranov, W., 1975.Potential Fields and Their Transformations in Applied Geophysics.Gebruder Borntraeger, Berlin, 151. Blakely, R.J., 1995.Potential Theory in Gravity and Magnetic Applications.Cambridge University Press, Cambridge. Cooper, G., 2004.The Stable Downward Continuation of Potential Field Data.Exploration Geophysics, 35(4):260-265.doi: 10.1071/EG04260 Fedi, M., Florio, G., 2002.A Stable Downward Continuation by Using ISVD Method.Geophys.J.Int., 151:146-156.doi: 10.1046/j.1365-246X.2002.01767.X Fedi, M., Florio, G., 2011.Normalized Downward Continuation of Potential Fields within the Quasi-Harmonic Region.Geophysical Prospecting, 59(6):1087-1100.doi: 10.1111/j.1365-2478.2011.01002.X Gao, Y.W., Luo, Y., Wen, W., 2012.The Compensation Method for Downward Continuation of Potential Field from Horizontal Plane and Its Application.Chinese J.Geophys., 55(8):2747-2756 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQWX201208027.htm Liu, D.J., Hong, T.Q., Jia, Z.H., et al., 2009.Wave Number Domain Iteration Method for Downward Continuation of Potential Fields and Its Convergence.Chinese J.Geophys., 52(6):1599-1605(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQWX200906023.htm Ma, G.Q., Liu, C., Huang, D.N., et al., 2013.A Stable Iterative Downward Continuation of Potential Field Data.Journal of Applied Geophysics, 98:205-211.doi: 10.1016/j.jappgeo.2013.08.018 Pasteka, R., Karcol, R., Kusnirak, D., et al., 2012.REGCONT:A Matlab Based Program for Stable Downward Continuation of Geophysical Potential Fields Using Tikhonov Regularization.Computers & Geosciences, 49:278-289.doi: 10.1016/j.cageo.2012.06.010 Pawlowski, R.S., 1995.Preferential Continuation for Potential-Field Anomaly Enhancement.Geophysics, 60(2):390-398.doi: 10.1190/1.1443775 Trompat, H., Boschetti, F., Hornby, P., 2003.Improved Downward Continuation of Potential Field Data.Exploration Geophysics, 34:249-256.doi: 10.1071/EG03249 Wang, G.C., Xu, Y.X., Chen X.J., et al., 2015.Three-Dimensional Geological Mapping and Visualization of Complex Orogenic Belts.Earth Science, 40(3):397-406 (in Chinese with English abstract). Xu, S.Z., 2006.The Integral-Iteration Method for the Continuation of Potential Fields.Chinese J.Geophys., 49(4):1176-1182(in Chinese with English abstract). doi: 10.1002/cjg2.928 Xu, S.Z., Yang, J.Y., Yang, C., et al., 2007.The Iteration Method for Downward Continuation of a Potential Field from a Horizontal Plane.Geophysical Prospecting, 55(6):883-889.doi: 10.1111/j.1365-2478.2007.00634.X Yu, J.J., Wang, G.C., Xu.Y.X., et al., 2015.Constraining Deep Geological Structures in the Three-Dimensional Geological Mapping of Complicated Orogenic Belts:A Case Study from the Karamay Region, Western Junggar.Earth Science, 40(3):407-418 (in Chinese with English abstract). Zeng, X.N., Li, X.H., Liu, D.Z., et al., 2011.Regularization Analysis of Integral Iteration Method and the Choice of Its Optimal Step-Length.Chinese J.Geophys., 54(11):2943-2950(in Chinese with English abstract). Zeng, X.N., Li, X.H., Su, J., et al., 2013.An Adaptive Iterative Method for Downward Continuation of Potential-Field Data from a Horizontal Plane.Geophysics, 78(4):J43-J52.doi: 10.1190/geo2012-0404.1 Zhang, H., Chen, L.W., Ren, Z.X., et al., 2009.Analysis On Convergence of Iteration Method for Potential Fields Downward Continuation and Research on Robust Downward Continuation Method.Chinese J.Geophys., 52(4):1107-1113(in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DQWX200904029.htm Zhang, H.L., Ravat, D., Hu, X.Y., 2013.An Improved and Stable Downward Continuation of Potential Field Data:The Truncated Taylor Series Iterative Downward Continuation Method.Geophysics, 78(5):75-86.doi: 10.1190/geo2012-0463.1 高玉文, 骆遥, 文武, 2012.补偿向下延拓方法研究及应用.地球物理学报, 55(8):2747-2756. doi: 10.6038/j.issn.0001-5733.2012.08.026 刘东甲, 洪天求, 贾志海, 等, 2009.位场向下延拓的波数域迭代法及其收敛性.地球物理学报, 52(6):1599-1605. http://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ201304022.htm 王国灿, 徐义贤, 陈旭军, 等, 2015.基于地表地质调查剖面网络基础上的复杂造山带三维地质调查与建模方法.地球科学, 40(3):397-406. http://www.earth-science.net/WebPage/Article.aspx?id=3033 徐世浙, 2006.位场延拓的积分迭代法.地球物理学报, 49(4):1176-1182. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200604032.htm 郁军建, 王国灿, 徐义贤, 等, 2015.复杂造山带地区三维地质填图中深部地质结构的约束方法——西准噶尔克拉玛依后山地区三维地质填图实践.地球科学, 40(3):407-418. http://www.earth-science.net/WebPage/Article.aspx?id=3181 曾小牛, 李夕海, 刘代志, 等, 2011.积分迭代法的正则性分析及其最优步长的选择.地球物理学报, 54(11):2943-2950. doi: 10.3969/j.issn.0001-5733.2011.11.024 张辉, 陈龙伟, 任治新, 等, 2009.位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究.地球物理学报, 52(4):1107-1113. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200904029.htm -
下载:
点击查看大图
图(5)
计量
- 文章访问数: 6012
- HTML全文浏览量: 2298
- PDF下载量: 32
- 被引次数: 0
