Reassessing Darcy' Law on Water Flow in Porous Media
-
摘要: 目前在地下水渗流研究领域公认的是：当雷诺数Re<(1~10)时，达西线性定律是描述地下水渗流运动的最基本方程，地下水流动的数学问题都可以基于该线性方程而导出.通过对当年达西实验数据的再分析以及利用透水石孔隙介质进行的渗流实验发现：即使在雷诺数Re<(1~10)的条件下，地下水渗流也不服从达西线性定律，而是呈现出随着雷诺数的增大，水流阻力也在逐渐增大，孔隙介质中的地下水渗流服从非线性渗流规律.达西线性渗流定律只是对斜率变化不大的非线性渗流规律的近似表征.Abstract: The shared understanding of law on movement of groundwater is that linear Darcy's law is the most basic equation of groundwater seepage. All the mathematical problems of groundwater flow can be derived based on Darcy's law if the the Reynolds number is less than a certain value between 1 and 10 (Re < (1-10)). The experimental data obtained by Darcy are analysed again and similar seepage experiments are carried out with permeable stone porous media. Both results show that even though the Reynolds number is less than a certain value between 1 and 10 (Re < (1-10)), the movement of groundwater would not obey Darcy's law but the nonlinear law. As the Reynolds number increases, the seepage friction grows gradually. It is concluded that Darcy's linear law is the approximate description of nonlinear law when the change of slope is small.
-
Key words:
- seepage /
- Darcy's law /
- linear /
- nonlinear /
- ground water
-
图 3 渗流实验装置
1.供水箱；2.离心泵；3.阀门；4.压力传感器；5.透水石；6.测流容器；7.数据采集器
Fig. 3. Seepage experimental setup
图 4 d=0.25 mm透水石Re-K变化曲线
Fig. 4. Relationship between Re and K on water flow in permeable stone (d=0.25 mm)
图 5 d=0.178 mm透水石Re-K变化曲线
Fig. 5. Relationship between Re and K on water flow in permeable stone (d=0.178 mm)
表 1 Darcy定律适用范围(据Bear, 1983)
Table 1. Application of Darcy's law
Darcy定律成立 Darcy定律不成立 Re < (1~10) (1~10) < Re < 100 Re>100 层流区 过渡区 紊流区 粘滞力起主导作用 粘滞力、惯性力并存 惯性力起主导作用 
下载: 导出CSV
表 2 达西实验成果(粒径d=0.77 mm)
Table 2. Results of Darcy's experiments (d=0.77 mm)
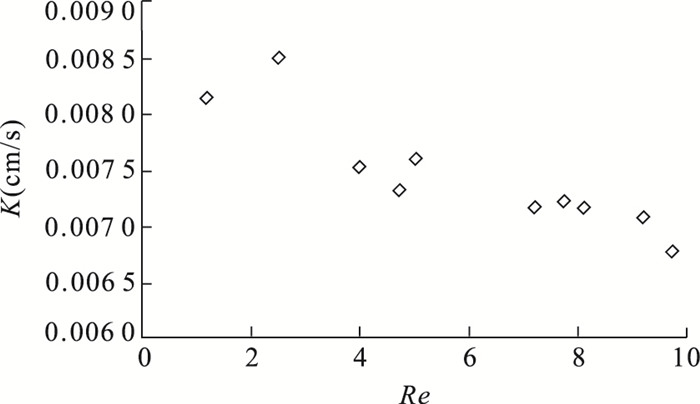
渗透流量Q(l/min) 水头差ΔH(m) 渗透流速u(cm/s) 水力梯度J 渗透系数K(cm/s) 雷诺数Re 3.60 1.11 0.016 1.91 0.008 1 0.12 7.65 2.26 0.033 3.90 0.008 5 0.25 12.00 4.00 0.052 6.90 0.007 5 0.40 14.28 4.90 0.062 8.45 0.007 3 0.47 15.20 5.02 0.066 8.66 0.007 6 0.50 21.80 7.63 0.094 13.16 0.007 2 0.72 23.40 8.13 0.101 14.02 0.007 2 0.77 24.50 8.58 0.106 14.79 0.007 2 0.81 27.80 9.86 0.120 17.00 0.007 1 0.92 29.40 10.89 0.127 18.78 0.006 8 0.97 注：渗透断面直径D=0.35 m；渗流长度L=0.58 m；表中Q、h的数据引自达西原著译本(Darcy and Bobeck, 2004)第457页，u、J、K、Re为相应的计算值.
下载: 导出CSV
表 3 粒径d=0.25 mm透水石的渗流实验数据
Table 3. Results of experiments in permeable stone (d=0.25 mm)
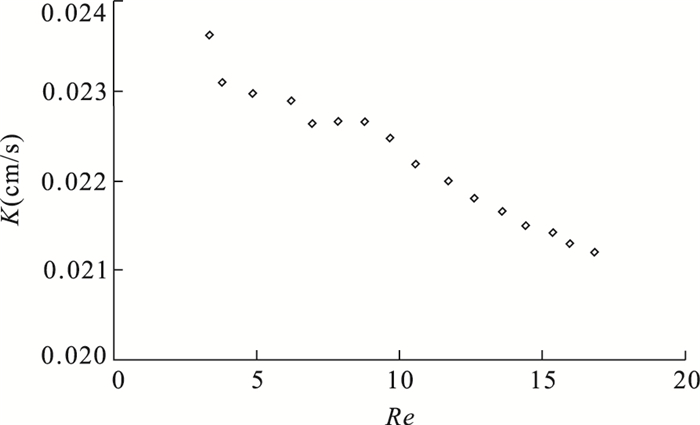
渗透流量Q(mL/s) 水头差ΔH(cm) 水力梯度J 渗透流速u(cm/s) 雷诺数Re 渗透系数K(cm/s) 3.23 46.28 6.61 0.156 3.34 0.023 6 3.64 53.45 7.64 0.176 3.77 0.023 1 4.67 68.91 9.84 0.226 4.83 0.023 0 5.98 88.54 12.65 0.289 6.18 0.022 9 6.67 99.82 14.26 0.323 6.90 0.022 6 7.56 113.07 16.15 0.366 7.81 0.022 6 8.46 126.50 18.07 0.409 8.75 0.022 6 9.31 140.33 20.05 0.450 9.63 0.022 5 10.17 155.39 22.20 0.492 10.52 0.022 2 11.32 174.24 24.89 0.548 11.70 0.022 0 12.14 188.74 26.96 0.587 12.55 0.021 8 13.12 205.36 29.34 0.635 13.57 0.021 6 13.91 219.19 31.31 0.673 14.38 0.021 5 注：渗透断面面积A=20.67 cm2；渗流长度L=7 cm；表中Q、h为实验观测值，u、J、K、Re为相应的计算值，h的测试精度为±1 mm，Q的测试精度为±3.8 mL，表 4同.
下载: 导出CSV
表 4 粒径d=0.178 mm透水石的渗流实验数据
Table 4. Results of experiments in permeable stone (d=0.178 mm)
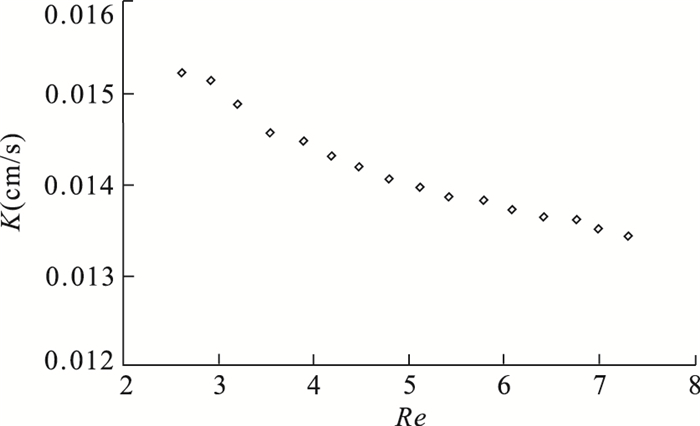
渗透流量Q(mL/s) 水头差ΔH(cm) 水力梯度J 渗透流速u(cm/s) 雷诺数Re 渗透系数K(cm/s) 3.10 68.95 9.85 0.150 2.59 0.015 2 3.49 78.05 11.15 0.169 2.91 0.015 1 3.82 87.00 12.43 0.185 3.19 0.014 9 4.22 98.10 14.01 0.204 3.52 0.014 6 4.64 108.65 15.52 0.225 3.88 0.014 5 4.98 117.95 16.85 0.241 4.16 0.014 3 5.36 127.90 18.27 0.259 4.47 0.014 2 5.73 138.00 19.71 0.277 4.78 0.014 1 6.11 148.20 21.17 0.296 5.10 0.014 0 6.49 158.50 22.64 0.314 5.41 0.013 9 6.91 169.40 24.20 0.335 5.77 0.013 8 7.28 179.65 25.66 0.352 6.07 0.013 7 7.67 190.45 27.21 0.371 6.40 0.013 6 8.10 201.55 28.79 0.392 6.76 0.013 6 8.38 210.30 30.04 0.406 7.00 0.013 5 8.76 220.90 31.56 0.424 7.31 0.013 4
下载: 导出CSV
-
Bear, J., 1983. Dynamics of Fluids in Porous Media. Translated by Li, J.S., Chen, C.X. . China Architecture and Building Press, Beijing, 95-97 (in Chinese). Chen, C.X., Lin, M., 1999. Dynamics of Groundwater. China University of Geosciences Press, Wuhan, 3-12 (in Chinese). Darcy, H., Bobeck, P., 2004. The Public Fountains of the City of Dijon. Kendall/Hunt Publishing Company, Debuque. http://www.cqvip.com/Main/Detail.aspx?id=11988286 Forchheimer, P., 1901. Wasserbewegung Durch Boden. Z. Ver. Deutsch. Ing., 45: 1782-1788. Li, J., Zhan, H., Huang, G., 2011. Applicability of the Linearized Governing Equation of Gas Flow in Porous Media. Transport in Porous Media, 87(3): 815-834. doi: 10.1007/s11242-011-9720-2 Li, J., Huang, G.H., Wen, Z., et al., 2012. A Laboratory Experiment on Radial Non-Darcian Flow in Confined Aquifer under Steady-State Conditions. Journal of Hydraulic Engineering, 43(1): 76-83 (in Chinese with English abstract). http://en.cnki.com.cn/Article_en/CJFDTOTAL-SLXB201201013.htm Izbash, S.V., 1931. O Filtracii V Krupnozernistom Materiale. Leningrad, Russian. Mathias, S.A., Todman, L.C., 2010. Step-Drawdown Tests and the Forchheimer Equation. Water Resources Research, 46(7): 1-9. doi: 10.1029/2009WR008635 Wen, Z., Huang, G.H., Zhan, H.B., 2009. A Numerical Solution for Non-Darcian Flow to a Well in a Confined Aquifer Using the Power Law Function. Journal of Hydrology, 364(1-2): 99-106. doi: 10.1016/j.jhydrol.2008.10.009 Wen, Z., Huang, G.H., Zhan, H.B., 2011. Non-Darcian Flow to a Well in a Leaky Aquifer Using the Forchheimer Equation. Hydrogeology Journal, 19(3): 563-572. doi: 10.1007/s10040-011-0709-2 Bear, J., 1983. 多孔介质流体力学. 李竞生, 陈崇希译, 北京: 中国建筑工业出版社, 95-97. 陈崇希, 林敏, 1999. 地下水动力学. 武汉: 中国地质大学出版社, 3-12. 李健, 黄冠华, 文章, 等, 2012. 承压含水层中非达西径向稳定流动抽水模拟试验. 水利学报, 43(1): 76-83. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201201013.htm -
点击查看大图
计量
- 文章访问数: 14555
- HTML全文浏览量: 309
- PDF下载量: 2238
- 被引次数: 0
