FCT ALGORITHM FOR CONVECTION-DOMINATED SOLUTE TRANSPORT IN UNSATURATED SOIL
-
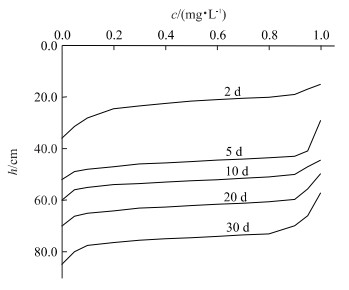
摘要: 描述非饱和土壤中溶质运移的对流弥散方程可分成两部分: 对流部分用通量校正运移(FCT) 算法求解; 弥散部分用常规的隐式差分方法求解.FCT算法包括两个阶段, 一个是低阶运移阶段, 这一阶段的解, 可能会引进过量的数值弥散; 另一个是高阶通量校正阶段, 通过对反扩散通量进行校正(限定), 可有效地消除数值弥散和数值振荡.而水体积分数用FUCG方法求得, 能保持质量守恒.通过数值例子验证了FCT算法的有效性.Abstract: Convection-dispersion equation describing convection-dominated solute transport in unsaturated soil may be divided into two parts: convection and dispersion. They are resolved by the FCT (flux-corrected transport) algorithm and conventional alternate direction implicit finite difference method, respectively. The FCT algorithm includes two phases: one is low-order transport, in which excessive numerical diffusion may be introduced; the other is high-order flux-corrected, in which numerical dispersion and oscillation can be effectively eliminated through correcting (limiting) antidiffusion flux. Moreover, the moisture content is obtained by FUCG algorithm, which is able to conserve the mass balance. At last, the effectiveness of FCT algorithm is verified by the numerical examples.
-
Key words:
- unsaturated soil /
- convection-dominated /
- FCT algorithm
-
[1] Boris J P, Book D L. Flux-corrected transport. Ⅰ : SHASTA, a fluid transport algorithms[J]. J Comput Phys, 1973, 11: 38-54. doi: 10.1016/0021-9991(73)90147-2 [2] Book D L, Boris J P. Flux-corrected transport. Ⅱ : generalization of the method[J]. J Comput Phys, 1975, 18: 248-283. doi: 10.1016/0021-9991(75)90002-9 [3] Zalesak S T. Fully multidimensional flux-corrected transport algorithms for fluid[J]. J Comput Phys, 1978, 31: 335-362. [4] Hills R G, Fisher K A, Kirkland M R, et al. Application of flux-corrected transport to the Las Cruces Trench site [J]. Water Resour Res, 1994, 30(8): 2377-2385. doi: 10.1029/94WR01216 [5] Kirkland M R, Hills R G, Wierenga P J. Algorithms for solving Richards' equation for variably saturated soils[J]. Water Resour Res, 1992, 28(8): 2049-2058. doi: 10.1029/92WR00802 [6] Tseng P H, Jury W A. Comparison of transfer function and deterministic modeling of area-average solute transport in a heterogeneous field[J]. Water Resour Res, 1994, 30 (7): 2051-2063. doi: 10.1029/94WR00752 -
下载:
点击查看大图
图(1)
计量
- 文章访问数: 3670
- HTML全文浏览量: 302
- PDF下载量: 9
- 被引次数: 0
